学習塾ロジム　今週の1問by 学習塾ロジム

分数倍を使いこなせますか？

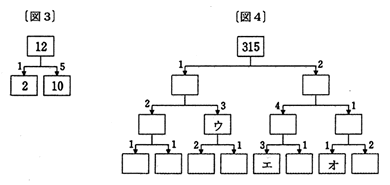
図3、図4は、数を矢印についている比に分けていく様子を表しています。たとえば、図3の場合、12が1：5に分かれて、2と10になります。図4のウ、エ、オに入る数はそれぞれいくつですか。（2008サレジオ学院中より一部抜粋）

ただの比の計算ですが、すべて求める必要はありません。

　ウ63
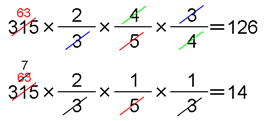
　エ126
　オ14

　実際に2008年にサレジオ学院中学校で出題された算数の問題（しかも最後の設問）です。

数字を順に比例配分していくだけですし、途中で分数や小数が出てくることもありません。時間さえ気にしなければ、誰も「難しい」とは感じることがないでしょう。

しかし、これが実際の入試問題なのです。日ごろから数の感覚（倍数、比、およその数の見当）が磨かれていないと、無駄に時間を費やしてしまう、もしくはつまらないミスで正答に至れない1問に値し、意外にも受験生の正答率に差が出たことでしょう。

（ちなみに、この問題を書きながらではないと処理できないようでは、比の感覚が弱いと言わざるを得ません。ぜひ、暗算によって数秒で処理できるようになって下さい。）

ウについて。
「315を1：2に分けたうちの1に当たる数」は、「315を3個に分けたうちの1個分」ということなので、315÷3×1＝105です。

次に、ウはこの「105を2：3に分けたうちの3に当たる数」ですから、同様にして「105を5個に分けたうちの3個分」となり、105÷5×3＝63と求められます。

さて、ここで気づいたかもしれませんが、比例配分は分数と考え方が同じです。

たとえば、「ＡをＢ：Ｃに分けたうちのＢに当たる数」＝「Ａを（Ｂ＋Ｃ）個に分けたうちのＢ個分」ですから、式としてはＡ÷（Ｂ＋Ｃ）×Ｂとなり、分数を利用すると結局次のように表せます。

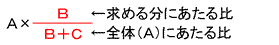
このように、比例配分された量を、分数を使って求める方法を「分数倍」といいます。特に、図形の中で比を使っていくときなどで威力を発揮します。

これを使って、エとオを計算すると、次のように求められます。

-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています～

1.

2.
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー

桐朋中より比の基本問題。比べる対象の変化に注目します。

3つの袋Ａ，Ｂ，Ｃがあります.まずはじめにＡには青い玉が，ＢとＣには白い玉がはいっていて、３つの袋に入っている玉の個数の比は6:3:1でした。ＡからＣへ（ア）個，ＢからＣへ（イ）個の玉を移したら, 3つの袋に入っている玉の個数の比は7:3:5になりました。さらにＡとＢからＣへそれぞれ6個の玉を移したら,Ｃに入っている青い玉と白い玉の個数の比は7:10になりました。

（１）（ア）と（イ）にあてはまる数の比を求めなさい。
（２）省略　　　　　　　　　　　　　　　　　　(桐朋中）

変わらないものがあります。

やりとりの後、玉の合計に変化していないので、問題文で与えられている比「 6:3:1」と「 7:3:5」の和も変化がないようにそろえます。
前：18:9:3
後:14:6:10
この比を見比べるとＡからＣへは4,BからＣへは3だけ移したことが読みとれる。
答:（ア）:（イ）=4:3

比とは文字通り比較です。比べる対象の変化にたいして敏感にならなくてはいけません。具体的には、変化したものと変化していないものをしっかりと区別して処理することが必要になってきます。小学生レベルでは「和一定」「差一定」「和も差も変化」の3通りが明確に区別され、つまり生徒でも見分けが用意な形で出題されますので、それぞれに独特な解法をしっかりと確認しておきましょう。

作業の過程にとらわれすぎず、結果の意味を考えましょう。

2つのコップに同じ量のミルクとコーヒーが入っています。大さじ４はい分のミルクをすくって、コーヒーの入っているコップに入れてよくかきまぜます。

つぎに、このコーヒーの入っていたコップから大さじ４はい分をすくって、ミルクの入っているコップに入れて、よくかきまぜます。
この作業の後、ミルクのコップの中のコーヒーの割合とコーヒーのコップの中のミルクの割合とでは、どちらが大きいでしょうか。

結果の意味を良く考えましょう。

2つの作業の結果、2つのコップに入っている液体の量は変わりません。

2つのコップともコーヒーとミルクが混ざっていますが、結果液体の量が同じということは、
ミルクのコップからコーヒーのコップへと移動したミルクの量と
コーヒーのコップからミルクのコップへと移動したコーヒーの量は同じ量です。

つまり、コーヒーとミルクがともに10リットルあったとすると、もしミルクが1リットルだけコーヒーのコップに移動したとすると、
同じ量のコーヒーがミルクのコップに戻ってきているということになります。

よって、コーヒーのコップの中のコーヒーに対するミルクの割合と
ミルクのコップの中のミルクに対するコーヒーの割合は同じです。

作業を直感的にとらえると、コーヒーのコップの中のミルクの割合の方が大きく感じます。

コーヒーの中に入れたミルクは純度100％のもので、ミルクの中にかえってくる同じ量の液体はコーヒーとミルクが混ざったものだからです。

直感と実際の差は、計算によって確認することが出来ますが、
本問のポイントは作業の流れをきちんとイメージすることです。

混ぜ終わった液体をきちんとイメージできれば簡単な問題です。
細かい点としては、液体の混合の問題では、
「混合液」のイメージを下の図１のように考える子供が多いのですが、
図2のようにとらえると「割合」として扱いやすくなります。

濃さには食塩の濃さと水の濃さの２つの見方があります。

10％の濃さの食塩水が100グラムあります。この食塩水を70％の濃さにするためには食塩をどれだけ加えればよいですか。

ノーヒントです。
　

10％の濃さの食塩水100グラムには食塩が10グラム、水が90グラム入っています。

ここに食塩を加えるわけですから水の量は変わりません。

70％の食塩水というのは、食塩水全体の重さに対して、食塩が70％を占めているということですが、水を中心に考えると、食塩水全体の重さに対して水が30％を占めているということもできます。

つまり、新たに作られる濃さ70％の食塩水とは、水90グラムが全体の30％を占める食塩水ということができるのです。

90グラムが全体の30％ですから、全体は90÷0.3＝300グラムになります。
現在全体で100グラムですから、差の200グラム分だけ食塩を加えればよいことがわかります。

出来上がる食塩水は全体で100＋200＝300グラム、食塩は10＋200＝210グラムとなり、その濃さは210÷300＝0.7となり問題文の指示通りの食塩水が出来たことが確認できます。

答え：200グラム

食塩の濃さに関する解法は様々なものがありますが「濃さ」のイメージをしっかりと持たせることと食塩の濃さだけでなく、「水の濃さ」という視点を持つことが大切です。
食塩の濃さに限らず、全体を構成する要素の中で見落としがちなものは何かということを考える姿勢は大切です。
ふたのある容器に水を入れる問題で、水の体積だけでなく、水の入っていない部分の体積に注目するといった考え方です。
補集合に着目するということですね。

今週は麻布中学算数入試より1問です。

容器A に食塩水が400g入っています。これを空の容器BとCに200gずつ入れ、さらにBには食塩を10g、Cには水を100g入れてよくかき混ぜました。次 にB、Cから食塩水を210gずつAにもどしてよくかき混ぜたところ、最初と同じ濃さの食塩水ができました。この食塩水の濃さは何％ですか。ただし、濃さ とは食塩水の重さに対する食塩の重さの割合のことです。　　　　　　　　　　　　　　　　　　　　　　　　　　

（麻布中） 　　

「食塩水を混ぜる問題と言えば」で機械的に解き始めてしまうとお終いです。

容器Aの食塩水400gに含まれる食塩を【2】とおくと、（＊以下、【 】を用いて比を表す）
最初の作業で分けられた容器Bと容器Cにそれぞれ食塩が【1】ずつ含まれることになる。

ここで、容器Bに食塩を10g加えると結果として
（【1】＋10）gの食塩が容器Bの中に残る。

そして、容器Cに水100g加えると、食塩水全体は
200＋100＝300g
になる。この中に10gの食塩が含まれていることになる。

以上より、容器Bから戻される210gの食塩水の中には
【1】＋10g
の食塩が含まれ、
（容器Aには200＋10＝210gしか食塩水がないので、含まれる食塩はすべて戻される）
容器Cから戻される210gの食塩水の中には
【1】×210/300＝ 【0.7】
の食塩が含まれる。
容器Aに戻された食塩水は420gであり、
これが最初の食塩水と同じ濃さであるからこの戻された食塩水に含まれる食塩は
【2】×420/400＝ 【2.1】　　となる。

よって（【1】＋10g）＋ 【0.7】 ＝【 2.1】　　　という関係が成立する。
これより
【0.4】＝10g
となる。

はじめの食塩水に含まれていた食塩は【2】であるから、
10÷0.4×2＝50g
となる。
よって、食塩水の濃さは
50÷400×100＝12.5％
となる。

答え　 12.5％

この問題の難しいところは、一見普通の濃度の 問題に見えるところです。

この年（平成15年度）の麻布中の算数は、異例の1番小問題4問というスタート。
長いリード文と積み重ねていくタイプの小問が並ぶ
通常の形式とは違った出題に戸惑った受験生も多数でした。

小問ということですが、内容はさすが麻布中。
すべてがパターン解法では太刀打ちできないものでした。

問題をしっかり読み、条件を書き出す。その書き出し方も重要。
正確で用途にあった形の線分図など、問題文をよく読み、必要な形で整理する能力が問われています。
基本をあやふやにしたままに、
試行錯誤タイプの麻布対策だけをしてきた受験生を、きちんと落とす良問ぞろいでした。

本問は、なにも考えずに天秤図を書き出してスタートすると迷路に迷い込みます。
・時間経過に沿って出 来事を整理する。
・数式化して整理し、比較してみる。
という算数においてもっとも基本的な作業を丁寧に行うことが必要です。

～今回の問題から導かれる出題校からのメッセージ～
・麻布でも地道な作業をする能力は重視します。

御三家レベルでは、計算問題や小問は、受験生のレベルからすると必要ないと判断されることが多く、出題も少ないのですが、本問においては反射神経でとくだ けではなく、丁寧な作業を毎回きちんと、すばやく行うという気構えが必要だと言えます。

ここ数年、麻布中の算数は地道な数え上げや当てはめなどの地道な作業を伴う問題が多くなって気ました。もちろん、それぞれに高度なセンスが求められるもの ではありますが、かつてのような「ひらめき」への偏りはなくなっています。

麻布中志願者の典型的な志向として、洗練された切れ味鋭い解法を求めるというものがありますが、その質実な能力を 麻布中が求め始めたのは明らかです。

夢見る数多くの未来の麻布志願者に、麻布受験者になる覚悟を問うているともいえます。
あらゆる問題で丁寧な読み込み、精密な計算能力、書き出しと数え上げが求められます。

世間一般の自由・洗練なイメージのみで麻布中を志願している子供たちには、
一度取り組ませてあげることで麻布中の本当の姿を確認させることのできるメッセージ性のある良問です。