学習塾ロジム　今週の1問by 学習塾ロジム

　有名事実を確認しよう【対象学年：5年生以上】





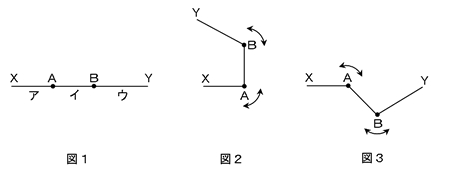
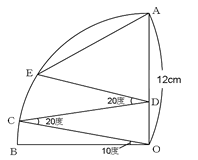
円Oの周上を毎秒12度動く点Ｐと毎秒6度動く点Ｑがあります。点Aを同時に出発し、矢印の方向に動くとき、三角形APQがはじめて直角三角形になるのは何秒後か。

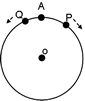
ありません。

三角形APQの辺のうち1つがOを通る、すなわち直径となったときに三角形APQは直角三角形になる。ＰとＱが180度離れるのは10秒後。このとき初めて三角形APQが直角三角形になる。

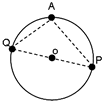
答え：10秒後

様々なテキストで、「三角形APQの辺のうち1つがOを通る、すなわち直径となったときに三角形APQは直角三角形になる」と解説されることがある本問ですが、なぜこのとき三角形が直角三角形になるのかを確認しておくことが大切です。

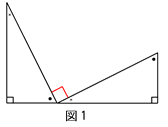
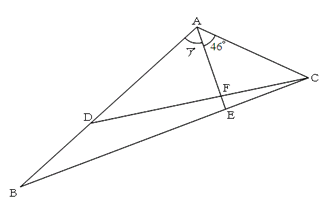
下の図のようにAOを通る補助線を引きます。

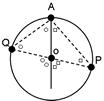
OA=OQなので三角形OQAは二等辺三角形となります。よって○は同じ角度となります。三角形OAPについても同様に□が同じ角度になります。それぞれの三角形の外角を考えると、○○＋□□が180度となっています。よって○+□は90度となります。三角形APQの内角のうち角PAQは○+□なので、三角形APQは直角三角形となります。

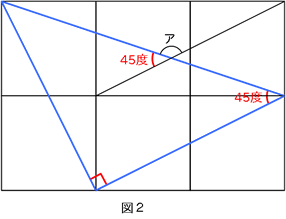
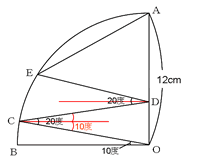
この考え方は下の図のようにPQが直径となっていなくても成り立ちます。

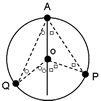
この図でわかるとおり、角PAQは中心角POQの半分の角度になっています。角PAQは中心角POQに対して、円周角とよばれ、常に中心角の半分の大きさになっています。円周角の定理と呼ばれるもので中学範囲ですが、全く同じ考え方で解く問題は頻出となっています。

-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています～

1.

2.
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー

　ひっかかりやすい積み木の個数【対象学年：４年生以上】





　下の図１は、小さな立方体をいくつか使ってつくった立体を、正面、上、右からそれぞれ見た図です。この場合、最も少なくて６個、最も多くて８個の立方体で作ることができます。
　では、図２のように見えるようにするには、最も少なくて何個の立方体が必要ですか。

　上から見た９か所すべてに立方体は必要でしょうか？

　１１個

　まず、図１が６個～８個でできることを考えてみましょう。
上から見た図の中に、正面、右から見た（積み上がった最大の）立方体の情報を書き込んでみると、次の図のようになります。

　さて、図２の場合を考えてみます。同じように、上から見た図の中に情報を書きこむと次のようになります。説明のために、ア～ケと名前をつけておきます。

　まず、１個しか積み上がって見えない「イ・オ・ク・エ・カ」は１個と考えられます。また、最大である３個積み上がっている場所はできるだけ少ない方がよいわけですから、「キ」が３個と考えられます。同様に、２個積み上がっている場所もできるだけ少ない方がよいわけですから、「ウ」が２個と考えれらます。
残った「ア・ケ」はあればよいわけですから、１個と考えられます。以上より、全部で１２個となります。

　しかし、実はこれは最小の個数ではありません。図のオをつくる４辺は、まわりに立方体がありさえすれば存在しますから、実はオは０個で構いません（オ意外の場所は、まわりに囲まれているわけではないので、そこに立方体がないと４辺ができあがらないため、１個以上必要になります）。
以上より、本当の最小の個数は１１個となります。

-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています～

1.

2.
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー

　２・２・３の直角三角形。





　下の図は、１辺が１cmの正方形を３つ合わせたものです。この図で、角アの大きさを求めなさい。

　見えない角度を作ります。

　135度

　まず、合同な直角三角形を下の図１のように向きを変えてならべると、間に直角があらわれます。
このことから、正方形をしきつめた図形の中には、見えない直角があらわれます。その一例が、正方形を６つしきつめたときの「２つ・２つ・３つの正方形の対角線」でできる直角三角形です。

　この問題も、図２のように６つの正方形をつくることで新たに直角二等辺三角形をつくることが可能です。
このパターンは頻出なわりに、意外にも正答率は高くありません。

　また、これと似た問題で、正方形（親）の中にできる傾いた正方形（子）も頻出ですね。

-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています～

1.

2.
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー

　円周率は、3.14でしょうか？

　下の図のように、１辺が５cmの正方形の画用紙に、半径５cmの四分円（円を４等分したもの）を書き、アとイの部分に分けました。
この画用紙に、でたらめに100個の砂の粒（大きさはどれも同じ）をまいたところ、アの中には22個、イの中には78個ありました。また、四分円の線の上には砂の粒はありませんでした。
　これについて、次の問いに答えなさい。

(1) このことから、イの面積は何平方cmであるとわかりますか。

(2) このことからわかる円周率は、いくつですか。

　広いほど、砂はたくさん入ります。

(1) 19.5平方cm
(2) 3.12

　まず、でたらめに100個の砂の粒をまいているので、これらは均等に散らばっていると考えることができます。
つまり、２倍の広さがあれば２倍の個数の砂が入るということですから、面積と砂の個数が比例することがわかります。
　ここで、正方形の中の100個の砂の粒のうち、イの部分には78個入っているので、正方形の面積の78/100倍がイの面積になります。

　また、このときの円周率を□とすると、下の式から□＝3.12と求められます。

　さて、円周率はよく3.14が用いられますが、これは本当の値ではありません。
円周率は無限に続く小数で、計算で扱うのが不便であることから、
近似値（近い値）として3.14を使っているにすぎないのです。

例えば、入試問題を見ても「円周率を３で計算しなさい」や「円周率を3.1とする」などがあるのはそのためです。
よく注意しましょう。

-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています～

1.

2.
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー

　「頂点決めの公式」

　図１は、ある立方体をＢ、Ｄ、Ｇを通る平面で切ったときの切り口を表したものです。また、図２は、この立方体を切る前に展開したときの図です。図２の中に図１の切り口を書き入れるとどのようになりますか。

ありません。

　図１に表された切り口は、面ＡＢＣＤ、面ＢＦＧＣ、面ＣＧＨＤの３つの面にあります。よって、図２の展開図に頂点を書き込んでいけばよいのです。頂点の決定のしかたには色々な方法がありますが、今回は「最も遠い２点」に注目してみます。
　たとえば、Ａから最も遠い点はＧです。ＡからＧへ隣り合う２つの面上を通って最短の道のりでいく場合、隣り合う２つの面を通る必要があります。これらを展開してみると、下の図のようになります。

このように、立方体で最も遠い２点は、隣り合う２つの面を合わせた長方形でも最も遠い２つの点となるのです。これが、頂点決めの公式です。
　最も遠い２点の組み合わせはＡ－Ｇ、Ｂ－Ｈ、Ｃ－Ｅ、Ｄ－Ｆですから、下の展開図で青い長方形に注目するとＡから最も遠い右上の点がＧ、Ｄから最も遠い右下の点がＦと決められます。また、緑の長方形に注目すると、ＧとＣが決められます。このようにして、隣り合う２つの面を合わせて考えると、ゲーム感覚（敵を探すように）ですべての頂点を決めることができます。

-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています～

1.

2.
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー

「固定」の威力を感じてください。

　長さ３㎝の棒ア、イと長さ４㎝の棒ウがつながってできたものを机の上におきます。図１は、これを真上から見たものです。また、棒どうしは図２や図３のように、連結部分Ａ、Ｂで折り曲げることができますが、棒と棒の間の角度を90度より小さくすることはできません。
　棒のはしを下の図１のようにＸ、Ｙとし、棒アのみを机の上に固定したとき、棒ウの先Ｙの動くことのできる部分の面積を求めなさい。ただし、棒の太さや連結部分のすき間を考えないものとします。

とりあえず、点Ｙの動く範囲を図示しなければ始まりません。

37.68（平方cm）

　まず、対称性を利用すれば、下側に曲げた場合のみを考え、その面積を２倍することでもとめる面積がわかります。ここで、棒イを固定して棒ウを動かすと、点Ｙは下の図Ⅰのような四分円の弧ＹＹ’を描きます。そして、棒イを回転させることで、図ⅡのようにＹとＹ’の行き先がわかります。よって、点Ｙの動くことのできる範囲は、下の図Ⅲのようになります。

　実際、面積を求めにいくときには、この複雑な図形がどのような簡易な図形（三角形やおうぎ形など）が組み合わされてできているのかを考えていきます。
　ここで、下の図Ⅳのように点Ｙ’が動いて描いた弧ＹＹ’は点Ａを中心とした四分円の弧なので、半径はＡＹ’となります。三角形ＡＢＹ’はＡＢ＝３㎝、ＢＹ’＝４㎝の直角三角形なので、ＡＹ’＝５㎝です。

　これより、求める面積は、以下のようにして求められます。

　よって、（７×７－５×５）×3.14÷４＝６×3.14となり、
　対称性から、６×3.14×２＝12×3.14＝37.68（平方cm）とわかります。

　このように、変化するものが２つ以上ある「複雑な動き」を考える場合、闇雲に動かす（試す）だけではなかなか正確に全体像をつかむことができません。場合の数などと同様に、１つを固定して考えるだけで、一気にわかりやすくなることは少なくありません。

-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています～

1.

2.
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー

本当の学習とは、教わる学習ではなく「自ら歩み出す学習」です。

下の図で、ＡＣの長さは１０cm、ＡＦの長さは６cmで、(ＡＤの長さ)：(ＢＤの長さ)＝３：２、(ＢＥの長さ)：(ＥＣの長さ)＝５：２であるとき、図のアの角度は何度ですか。

　・平行線の威力を感じてください。
　・気づく必要はありません。色々と試してください。

６７度

図１のように、与えられた情報を書き込むと、ＡＢとＢＥが異なる比ながらも「５」で揃います。

図1：

平行線にそって比が移動できる（相似の性質─ピラミッド）を利用すれば、図２のように新たに点Ｇを作ることで点Ｄを頂点とした新たなピラミッドが出来あがります。

図2：

このとき、三角形ＤＡＦと三角形ＤＧＣが相似であること（相似比３：５）から、
　辺ＣＧ＝６×（５／３）＝１０cm
とわかります。

つまり、△ＣＡＧは二等辺三角形となります。

さらに、ＡＦとＧＣが平行ですから、平行線の錯角を利用して

　角ＡＧＣ＝４６度となり、
　角ＣＡＧ＝角ＣＧＡ＝（１８０－４６）÷２＝６７度

とわかります。

　求める角アは、平行線の同位角によって角ＣＧＡと等しくなるので、答えは６７度となります。
　

-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています～

1.

2.
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー

前回に続き、情報に惑わされず、図形の本質を見抜くことが真の「力」です。

　下の図は四分円ＯＡＢの弧の上に点Ｃ、Ｅを、半径ＯＡ上に点Ｄをとり、それらを結んだものです。このとき、辺ＣＤの長さを求めなさい。ただし、角ＢＯＣ＝10度、角ＯＣＤ＝角ＣＤＥ＝20度です。

必要な情報を見抜いてください。

12cm

　角ＣＯＤ＝80度であることから、△ＯＣＤは二等辺三角形であることがわかります。

よって、ＯＣ＝ＣＤで、ＯＣは四分円の半径ですから、ＯＣ＝ＣＤ＝12cmであることがわかります。

　この解説のとおり、この問の答えを導くために「角ＣＤＥ＝20°」という情報は使いません。

受験テクニックを学んでいくと、どうしても与えられた情報（特に頻出のテクニックや知識に関わる情報）から答えを探っていくことが多いもので、もちろんそれが重要であることが多いのですが、逆にその情報に惑わされて本来の解答を導くポイントを見失う危険性があるのです。

　この問題であれば、「求められる角度から二等辺三角形に気づく」ということ以上に、
「ジグザグの線→平行線による分割」が頭から離れず、下の図のようにＯＢと平行な線を引き・・・
などと考え始めた人が多いのではないでしょうか。

--------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています～

1.

2.
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー

情報に惑わされず、図形の本質を見抜くことが真の「力」です。

　下の図は四分円ＯＡＢの弧の上に点Ｃをとり、点ＣからＯＡ、ＯＢにそれぞれ平行な線を引き、長方形ＯＤＣＥを作ったものです。このとき、辺ＤＥの長さを求めなさい。ただし、∠ＯＥＤ＝60度です。

60度は、重要でしょうか？

12cm

　辺ＤＥは、長方形ＯＤＣＥの対角線です。よって、ＤＥ＝ＯＣであり、辺ＯＣは四分円の半径ですから答えは12cmとなります。

　この解説のとおり、この問の答えを導くために「∠ＯＥＤ＝60度」という情報は使いません。

受験テクニックを学んでいくと、どうしても与えられた情報（特に頻出のテクニックや知識に関わる情報）から答えを探っていくことが多いもので、もちろんそれが重要であることが多いのですが、逆にその情報に惑わされて本来の解答を導くポイントを見失う危険性があるのです。

　この問題であれば、「ＤＥが長方形の対角線である」ということ以上に、「∠ＯＥＤ＝60度」が頭から離れず、ＯＥ：ＤＥ＝１：２だから・・・などと考え始めた人が多いのではないでしょうか。そのような人は、この問題が「ＢＥの長さを求めなさい」の方が意外と即答できたかもしれませんね。

ちなみに、ＢＥ＝ＯＢ－ＯＥ＝ＯＢ－ＤＥ÷２＝６cmです。

　余談ですが、60度にこだわらず下の図のようにどのような長方形を描いたとしてもＤＥ＝12cmということですね。

--------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています～

1.

2.
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー

限界を考えることは、意外と難しいものです。

正方形の向かい合う辺の真ん中の点どうしを結ぶと、２つの合同な長方形に分割できます。

さらに、その長方形の長い方の辺の真ん中の点どうしを結ぶことで、右の図のように正方形を
作ることができます。そして、これを1回の「操作」と呼ぶことにします。
　下の図は、1辺が1cmの正方形について、この操作を３回繰り返したものです。これについ
て次の問いに答えなさい。

問1　
上の図で、3回までの操作を行ったときの最も小さな正方形（色つき部分）と、それ以外の部分の面積比を求めなさい。

問2　
1を順に半分にしていくと、1/2　、1/4　、1/8　、1/16　、1/32　、1/64　、…となります。このような数のならびで、1番目を　1/2　とし、順に番号をつけていきます。つまり　1/64　　は6番目となります。この数のならびで、100番目までの数の和と1はどちらが大きいですか。上の図を参考にして考え、大きい方を答えなさい。

図の各正方形の1辺に注目してみましょう。

問1　1：63
問2　1

問1　

最も小さな正方形（色つき部分）ともとの大きな正方形は、相似比が1：８の正方形です。よって、面積比は1：64になるので、もとの正方形から最も小さな正方形（色つき部分）を除いた分は63になります。

問2　

実際、100番目の数を求めようとするのは、かなり厳しいでしょう（10番目でさえも、　　ですから）。

100個もたしていくわけですから、1くらい平気で超えそうですが…。

さて、ここで図をもとに考えてみましょう。もとの1辺1cmの方形の下の辺を「操作」によってで

きた正方形ごとに見てみましょう。すると、順に、1/2、1/4、1/8、1/16、1/32、1/64、・・・・　となりますが、

どれだけ操作を繰り返して分割していっても、絶対にもとの正方形の1辺を超えることはありません。
よって、たとえ何番目まで足したとしても、1の方が大きいのです（極限の考えは除きます）。

まとめ
　「ひたすら足しまくるのだから、1くらい超えるだろう」という、常識（？）を覆す問題です。

高校数学でで極限を学べば、ある程度当たり前に感じることのできる内容ですが、小中学生には少々想像しがたいことでしょう。特に、問題のような図を与えず、ただ言葉や文章だけで出題したとすれば、おそらく全て（に限りなく近い数）の子供たちが1の方が小さいと答えるのではないでしょうか。

しかし、そんなイメージがわきにくいことも、図を用いてみるとあっけなく納得できるのです。図の力とは偉大ですね。
（どんなに1に近づこうとも、常にそのゴールまでの半分しか進めないというもどかしさがわかるはずです）
　この問題を通して、不思議だと思い、少しでも算数や数学に興味をもってもらえたら嬉しい、そんな一問です。