2010年度入試シリーズ (4)鴎友学園女子中学校【算数】より
2010年度入試シリーズ (4)鴎友学園女子中学校【算数】より

ある中学校の図書館で、図書委員が本にラベルを貼る仕事をします。次のことがわかっています。
・1年生の委員は2年生の委員よりも6人多く、3年生の委員は2年生の委員よりも4人少ない
・委員1人が1日で貼る数は、2年生と3年生は同じ、1年生はその半分
・1年生だけではちょうど8日かかり、2年生だけではちょうど6日かかる
3年生だけでは何日かかりますか。

ラベルを貼るという「仕事」ですね。

9日

結局のところ、仕事算です。ただ、能力(仕事の速さ)は、委員1人あたり1日で貼る枚数と人数で決まるところに注意が必要です。
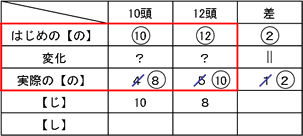
まず、1年生と2年生の委員1人あたりが1日に貼る枚数の比は、1:2で表せます。
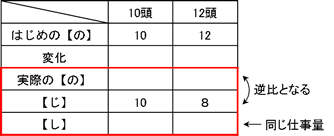
また、同じ仕事を1年生は8日、2年生は6日かかることから、逆比を利用して1年生と2年生の能力の比は3:4となることがわかります。
いま、1年生がア人、2年生がイ人だとすると、1×ア:2×イ=3:4となることから、ア:イ=3:2とわかります。
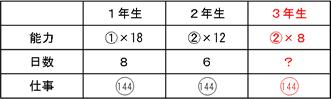
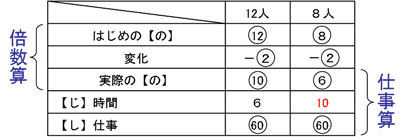
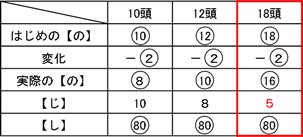
ここで、アとイの差が6人ですから、比1あたり6人となり、ア=18人、イ=12人となります。3年生の委員1人あたり1日で貼る枚数は2年生と同じ2で、人数は2年生より4人少ない8人なので、これらをまとめると下の表のようになります。
これより、144÷16=9日とわかります。
一見、単純な問題のようですが、委員1人あたりが1日で貼る枚数が異なることをどう処理するかで悩んだ受験生が多かったことでしょう。
1人あたりの単位仕事量が全員同じならば能力が人数比になるということを公式的に覚えていたのでは、意外にも歯が立たない問題です。
-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています~
1.
2.![]()
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー


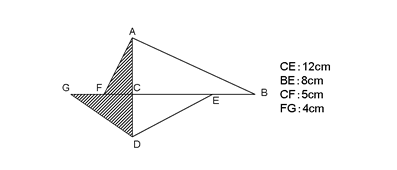
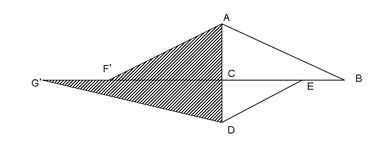
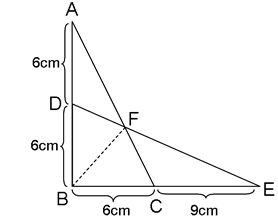

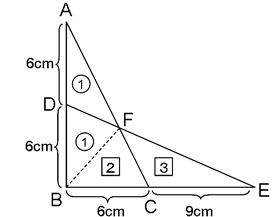
 は=11.25なのでもとめる三角形ABCと三角形DBFの面積の比は
は=11.25なのでもとめる三角形ABCと三角形DBFの面積の比は