学習塾ロジム　今週の1問by 学習塾ロジム

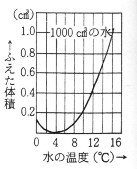
ストッパーには、良問がそろっています（平成16年度　女子学院中学校より）。

下の図で、長方形ＡＢＣＤの辺ＡＢの長さは４cm、辺ＢＣの長さは８cmです。
このとき、対角線ＡＣを１辺とし、点Ｄを通る長方形ＡＣＥＦの面積を求めなさい。

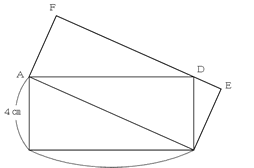
長方形ＡＢＣＤと長方形ＡＣＥＦ、どちらが大きく見えますか？
また、ルート記号は不要です（大ヒントかな？）。

32（平方cm）

ＡＣが長方形ＡＢＣＤの対角線であることから、三角形ＡＣＤ＝４×８÷２＝16（平方cm）とわかります。
ここで、三角形ＡＣＤは長方形ＡＣＥＦの半分であることがわかります。

（長方形ＡＣＥＦ＝ＡＣ×ＡＦ、三角形ＡＣＤ＝底辺ＡＣ×高さＡＦ÷２より）
よって、長方形ＡＣＥＦ＝16（平方cm）×２＝32（平方cm）となります。

解説を見てわかるとおり、なんてことない問題です。

しかし、時間が限られた（しかも入試本番で最高に緊張している）時間で処理しなければならないとしたら…？

まず、ＡＣの長さを求めようとして…、ＡＦの長さに注目して…となってしまうことでしょう。

入試問題には、このように一見簡単に見えるにもかかわらず、即答できず、思考を停止させる「ストッパー」が数多く存在します。
これこそまさに、良問の類といえるでしょう。

　さて、この問題を、見た目と同様に容易に処理するには、次の２点が必要です。
1）与えられた情報（辺の長さ）から、わかることは何か？
2）図形分割における、面積比の基本（←問題演習で身につけられます）

　仮に、この問題が即答できないとしても、長方形ＡＢＣＤと長方形ＡＣＥＦはどちらが大きいか？
くらい、意識して欲しいところです。

植物の育ち方と光の関係。多くの生徒が間違って理解しています。

同じ条件の畑で、ヒマワリやホウセンカの種をまき、その育ち方を調べました。これについて、次の問いに答えなさい。

問1　ヒマワリの種を図1のＡ、Ｂのようにまきました。その後の育ち方について正しいものを次のア～オから選び、記号で答えなさい。ただし、すべてＢと比べたときのＡのようすを表しています。

問2　図2のようにホウセンカの種をまき、数日後育って大きくなったあとでＸ－Ｙの断面を調べました。これについて、次の(1)、(2)に答えなさい。

　(1) Ｘ－Ｙの断面として、最も適当なものはどれですか。下図のア～ウから選び、記号で答えなさい。
　(2) (1)で選んだ断面について、～のホウセンカのうち最もくきが太いのはどれですか。数字で選び、番号で答えなさい。

「植物は、光が当たるほどよく育つ」と単純に思い込んでいませんか？

問1　ウ
問2　(1)ウ、(2)

問１　

植物は、「光合成」によって、光のエネルギーを得て、自ら養分を作り出すという特別なはたらきをしています
（正確に言えば、光のエネルギーを閉じ込めるために養分を作るわけですが…）。

　　太陽からの光は、この地球全体に届きます。つまり、単純に考えれば、この世界を植物が覆い尽くすほどエネルギーが盛んに作られることになります。では、想像してみてください。地面いっぱいに植物が茂っていたら…？

　　●ヒトが暮らす場所がなくなる？
　　●緑で土の水分が奪われ、地割れで地球がこわれる？
　　●むしろ、地球温暖化を防ぎ、暮らしやすくなる？

　　いいえ、そもそも植物が地面を覆い尽くすことはないのです。
　　
植物が生きていくためには、もちろん光が必要です。しかし、地球に届く光は限られています。つまり、増えすぎた植物どうしは、光の奪い合いを行うのです。簡単に言えば、限られた食料の中で、多数の動物が生きるには限度があるということと同じです。　　

この問いでは、Bに比べて密集したＡだと、光の当たりにくい場所ができ、十分に育つヒマワリが少なくなると考えられます。

しかし、多くの植物は生命のエネルギー源である光を心底求めています。そして、全エネルギーを光を浴びることを優先に使います。この結果、本来葉を大きくし、茎を太くし、効率よく光を浴びることを忘れて、光の当たりにくい植物は背丈をひたすら伸ばしてできる限り光を浴びようとする傾向にあるのです。

問2

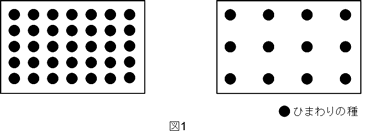
　同種の植物どうしで光を奪いあうわけですから、問1と同様に考えることができます。ここで、太陽の動きを考えてみると、東→南→西となります。つまり、右図のように光の当たりやすいところ（）、当たりにくいところ（）に分けられます。

よって、Ｘ－Ｙの断面を見れば、中央部分は光が当たりにくく、端の方は光がよく当たることがわかります。

光が不足するほど植物は背を伸ばそうとするわけですから、中央部分は背が高く、端の方は背が低くなるのです。また、このことより中央部分はくきが細く、端の方がくきは太くなります。

たしかに植物は、光が当たるほどよく育つのですが、それは茎の太さ、背丈、葉の大きさ、根のはり方などの総合バランスについてであって、この問題のように背丈だけで考えれば必ずしも「光が当たるほどよく育つ」とは言えないのです。

灘中より。問題文に明記されていない隠れた条件を使います。

2桁の整数が4つある。この4つの数のうちの2つの和と差を全部調べたら、和のうち最も大きいものは187で、最も小さいものは137であり、差のうちで最も大きいものは40で、最も小さいものは10である。4つの数のうち小さい方から2番目の数を答えよ。　（灘）

偶数と奇数をたすと奇数になります。

54つの2桁の整数を大きい順にＡ、Ｂ、Ｃ、Ｄとします。
問題文の条件は
Ａ+Ｂ＝187
Ｃ+Ｄ＝137
ＡｰＤ＝40
という式で表せます。

ここでＡとＢの和が187という奇数であることから、ＡとＢのいずれかが奇数であることがわかります。
よってＡとＢの差も奇数です。

同様に考えるとＣとＤの差も奇数です。
最小の差というのは、大きい順に並べたときのとなりとの差であるから（例えばＡｰＣが最小になることはない）4つの数のうちの2つの差の組み合わせで10となる候補はＢｰＣのみ。

よって、ＡとＢの差は11以上になるが、和が187でともに2桁の数という制約で考えると、Ａが99でＢが88という組み合わせしかない。
よって2番目に小さい数Ｃは88-10=78

答え78

いくつかの整数の和と差のヒントから元の数を考えるという問題です。

条件の与えられ方や題材（おもり、体重、テストの点）などは表面的に色々なバリエーションがありますが、ポイントは隠れた制限を見つけ出すことです。その主たるものが今回の偶奇と桁数の制限です。これらをつかってＡ+ＤとＢ+Ｃのどちらが大きいのかを判断したり、最大、最初の数を確定させたりします。

偶奇の性質の活用は、非常にシンプルなだけに思考から外れてしまいがちな難しい技術です。

「和や差から元の数を求める」という問題に出会ったときは、必ずチェックする項目として覚えておきたいものです。

「上手な足し算」を設計する力が問われます。

1，2，3，4，5の数字が書かれたカードが1枚ずつあります。これらのカードを使ってつくることのできる5桁の数すべての和を求めなさい。

全部で120通り。足し算をしていくには多すぎます。

5枚のカードを1回ずつ使うので、その並べ方は5×4×3×2×1＝120通りある。
これら120通りの5桁の数の各位を構成する数字に着目する。
120通りの一万の位には1,2,3,4,5が同じ回数ずつ使われている。つまり各数字24回ずつである。
千の位、百の位、十の位、一の位も同様。
つまり、すべての数の和は

（1×24+2×24+3×24+4×24+5×24）×10000+
（1×24+2×24+3×24+4×24+5×24）×1000 +
（1×24+2×24+3×24+4×24+5×24）×100+
（1×24+2×24+3×24+4×24+5×24）×10+
（1×24+2×24+3×24+4×24+5×24）
＝ （1×24+2×24+3×24+4×24+5×24）×11111=3999960
答え：3999960

効率的な数え上げを問う問題はその場での思考力を問わていると思われがちですが、
全く使った経験のない手法をその場で思いつくのはほとんど不可能です。

普段から、様々な問題に取り組み、模範解答で提示されている洗練された手法の仕組みをしっかりと確認していくことで蓄積されていくものです。

多くは、「数字を横ではなく縦に読む」つまり位ごとに整理していくという考えが根底にあるものです。答えがあっていただけで満足せず、様々な別解を探求する姿勢だけがこのような能力を高めることにつながります。

根拠をもって予想する≒仮説をつくって問題を解く練習を数多くしましょう

メダカは5月～8月の朝早い時間に産卵を行います。メダカが水草に産みつけた卵を、同じ数ずつ10℃,　20℃,　30℃,　40℃,　50℃の水温の水槽に入れ、それぞれ水温を一定にたもち、3週間の間に卵からかえった数をしらべました。その結果をグラフにしたのが下のグラフです。正しいグラフはどれですか。一つ選び、それを選んだ理由を説明しない。

予想する方法は、自分の知っていることと、与えられたヒントを組み合わせる以外にはありません。

ア

生徒A「メダカは25℃前後の水温でもっとも多く産卵すると習ったし、問題にも5月～8月に産卵すると書いている。つまり暖かくなるとたくさん卵がかえるのではないか。」

生徒B「ということは、グラフ（イ）だね。」

生徒A「ちょっとまって、でも水温40度って言えば普段入っているお風呂と同じくらいの温度だし、50度なんていったら卵はゆであがっちゃうんじゃないの？！」

と、わざとらしい会話ですが上のように「自分の知っていること」「常識」「文章中のヒント」を組み合わせます。
メダカについての学習範囲を覚えていないという理由でこの問題を放棄するようでは先は明るいとはいえません。

集合の全体を見渡す力が問われます

1001から3139までの数について、数字0が現れない数はいくつありますか。

4人の中から3人を選ぶ選び方と同じ手法ですね

区切って数えていきます。1001から2999を考えます。

1□□□、2□□□を考えたとき、0が現れないということは、□の中に1から9までの数字しかつかわれないということです。

よって1□□□は9×9×9=729通り、2□□□は9×9×9=729通りあるので合わせて1458通り。

3000から3110まではすべて0が使われている。3111から3139までを上と同じように考える。

つまり31□□で□に0を使わないというのは1から9までで構成されているということ。

十の位は1か2か3の3通り、一の位は9通りあるので3×9=27通り。

よって合計1458+27 =1485通り

ヒントの問題はだれもが一度は触れているもののはずです。

ポイントは全体から求めたい集合をのぞいたもの（補集合）を上手く活用するということです。

これは、本問のような場合の数だけでなく、求積問題などでも非常によく使われ、有用な視点です。

(全体から余分なものを求めて引くというもの）どちらに着目しても、答えにたどり着くことは可能なのですが、そこは出題者も意図していて計算量、難易度に大きく差がでるように設計します。

求めたいもの自体を、違った形に変形して求めることは可能か。問題の主旨を損なわずにすり替えることは可能か。という意識は常にもちながら問題に取り組むことが必要です。

「連続する整数」の持つ様々な性質に注目します。

8=3+5
45=13+15+17
45=5+7+9+11+13
のように連続する奇数の和で表すことができる整数があります。495を連続する奇数の和で表す方法をすべて書きなさい。

「連続する数」の扱いには共通の手法があります。

奇数の和が495という奇数になるので、足し算に使う数の個数は奇数となる。
また、連続する奇数個の奇数の和は、平均となる真ん中の奇数×個数で求めることができる。

495=3×3×5×11より、求める奇数の個数は3個、5個、9個、11個、15個、33個、45個・・・など495の約数個を考えればよい。

3個の場合、495÷3=165より真ん中は165となり、3つの奇数は163、165、167となる。

5個の場合、495÷5=99　より真ん中は99となり5つの奇数は95、97、99、101、103となる。

9個の場合、495÷9=55　より真ん中は55となり9つの奇数は47、49、51、53、55、57、59、61、63となる。

11個の場合、495÷11=45より真ん中は45となり11個の奇数は35、37、39、41、43、45、47、49、51、53、55となる。

15個の場合、495÷15=33より真ん中は33となり15個の奇数は19、21、23、25、27、29、31、33、35、37、39、41、43、45、47となる。

33個の場合、495÷33=15より真ん中のは15となるが、15を中心として33個の奇数を並べることはできない。（小さい方向に16個の奇数を並べようとすると0より小さい数が出てきてしまう。）

これ以上の連続する奇数を考えると同様になる。よって答えは、上記に示した5通り。

「連続する整数」の和というのは（最初+最後）×個数÷2という計算手法は有名ですが、その仕組みをしっかりと確認していないと、今回の応用は難しかったのではないでしょうか。
連続する整数の列において、（最初+最後）÷2の意味は平均です。棒グラフにしてみると直感でも理解できるはずです。また連続する数とその和というのは偶奇やその個数など以外と制約が多いことも覚えておきましょう。一見、条件が足りないように見えてもそれらの条件から答えを絞り込むことが可能となります。

「水に浮く」とはそもそも何を意味するのか。基本原則をおさえます。

ポリエチレンのふくろA～Cに、温度のちがう水（A…0℃、B・‥4℃、C…16℃）を同じ体積ずつ入れました。そして、右下の図のように、A～Cのふくろを10℃の水が入った水そうの中央に静かに入れました。A～Cのふくろはそれぞれどうなりますか。次のア～エから選びなさい。

ア　しずむ　イ　うく　 ウ　中央から動かない　エ　ういたりしずんだりする

「同じ体積あたりの重さ」（≒密度）という概念を理解してください。

A・・・ア
B・・・ア
C・・・イ

そもそも、「水に浮く、水に沈む」とはどういったことなのか確認します。
周囲の水に比べて、同じ体積で比べたときの重さが小さいときに物体は水に浮き、大きいときに物体は水に沈みます。

あえて思い切ったかんたんな言い方をすると、「水に比べて少しでもぎっしりと中身が詰まっているものは沈み、水にくらべ少しでも中身がスカスカなものは浮く。」とイメージすることができます。

水は4度の時が体積最少となります。重さは変わらないので、4度のときに密度最大（＝最も「ぎっしり」） になります。
（↑この文章の内容を一読してイメージできないようでは正直中学受験は厳しいと思います。）

このグラフのように、水の体積は4度を最少として（4度付近では）左右対称の形になります。したがって、4℃との差が大きいほど、体積は大きくなり、「スカスカ」になります。

では類題です。たとえば、ポリエチレンふくろに0℃の水をいれて、ふくろが浮きも沈みもしないで動かないのは、水そうの中の水が何度のときでしょう？わかりますよね？

麻布中より。倍数判定法の基本が高いレベルで問われます。

Ａは４けたの整数でそれぞれの位は同じ数字からなり、Ｂは４けたの整数でそれぞれの位は2種類の数字からなっています。ＡとＢの積を計算したら44448888になりました。ＡとＢを求めなさい。(麻布中）

「すべての位が同じ数字である整数」を割り切る数のうちの1つは「見た目」で簡単に見つかります。

すべての位の数が同じである4けたの整数Ａは1111の倍数となる。
Ａ＝1111×□となるからA×B=1111×□×Ｂ=44448888であることがわかる。

44448888÷1111=40008であるからＢ×□＝40008となる。

ここで40008＝4×10002であり40008=6×6668であり、 40008= 8×5001であることから、□の候補は6もしくは8となる。
□が6のときＢは6668、8のときは5001となるが、Ｂは2種類の数字のみでつくられる4けたの整数のなので6668となる。
よってＡ＝1111×6＝6666

答え：A＝6666,B=6668

基本的な倍数判定の知識をしっかりと自分のものとして、使いこなせていないとゴールまで簡単にはたどりつけません。

Aの約数1111の発見に関しては初見の問題としては少々難易度が高いですが、一度本問を解いておけば問題ないでしょう。
この問題は1番の（2）つまり素早く終わらせなくてはいけないもので、ポイントは40008が4の倍数であり、6の倍数であり、8の倍数であることの発見です。それぞれの倍数判定法はどの教科書にも載っている基本事項ですが、直接問われてはいない本問のような形式で素早くチェックするには相当量の練習で知識が定着している必要があるでしょう。

桐朋中より比の基本問題。比べる対象の変化に注目します。

3つの袋Ａ，Ｂ，Ｃがあります.まずはじめにＡには青い玉が，ＢとＣには白い玉がはいっていて、３つの袋に入っている玉の個数の比は6:3:1でした。ＡからＣへ（ア）個，ＢからＣへ（イ）個の玉を移したら, 3つの袋に入っている玉の個数の比は7:3:5になりました。さらにＡとＢからＣへそれぞれ6個の玉を移したら,Ｃに入っている青い玉と白い玉の個数の比は7:10になりました。

（１）（ア）と（イ）にあてはまる数の比を求めなさい。
（２）省略　　　　　　　　　　　　　　　　　　(桐朋中）

変わらないものがあります。

やりとりの後、玉の合計に変化していないので、問題文で与えられている比「 6:3:1」と「 7:3:5」の和も変化がないようにそろえます。
前：18:9:3
後:14:6:10
この比を見比べるとＡからＣへは4,BからＣへは3だけ移したことが読みとれる。
答:（ア）:（イ）=4:3

比とは文字通り比較です。比べる対象の変化にたいして敏感にならなくてはいけません。具体的には、変化したものと変化していないものをしっかりと区別して処理することが必要になってきます。小学生レベルでは「和一定」「差一定」「和も差も変化」の3通りが明確に区別され、つまり生徒でも見分けが用意な形で出題されますので、それぞれに独特な解法をしっかりと確認しておきましょう。