学習塾ロジム　今週の1問by 学習塾ロジム

頌栄より。対照実験から仮説を導く基本問題です。

サツマイモを半分に切って水栽培をし、芽や根がどこから出るかを調べた。イモができたとき、茎に近かった方をA、その反対側をBとして実験を行ったところ、(1)～(4)のような結果を得た。

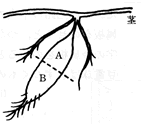
（1）Aの上下をそのままにして栽培すると、芽は上から、根は下から出た。
（2）Aの上下をさかさまにして栽培すると、芽は下から出、その根元から根が出た。（3）Bの上下をそのままにして栽培すると、芽は上から、根は下から出た。

（4）Bの上下をさかさまにして栽培すると、芽は下から出、その根元から根が出た。

問）
この実験から分かることを、 （a）芽の出かた　（b）根の出かた　それぞれについてまとめなさい。

(頌栄中・抜粋）

Aの部分とBの部分の違いはなんでしょうか。

（a)芽は上下の置きかたに関係なく、もともと茎に近かった部分から出る。

（b）根は、もともとの位置に関係なく、下に置いた部分から出る。

芽、根についてそれぞれ（1）～（4）の共通点を探します。

芽の置き方については、上下の置き方に無関係であることがわかる。
ここからは「気付かなくてはいけない」ところではあるが、そもそもAとBの部分は何が異なるかを考えると、
「もともと地中にあったときに茎に近かったかどうか」という点に着目できる。

この点に着目すれば、
切り取る前に最も茎に近かった場所から、芽が出ていることが分かる。

根については、単純に(1)～(4)の共通点を探すことで、下に置いた部分から根が出ていることが分かる。

～今回の問題より導かれる出題校からのメッセージ～
まず仮説をたてる方法を知る

科学の世界では常識であり、ロジカルシンキングの授業でも多く取り上げる「仮設を立てる」というテーマ。

多くの参考書や問題集、また授業でも取り上げられるこの種の問題ですが、
ではどうやって仮説をたてるのかということには全く触れていないのが実情ではないでしょうか。

仮説を立てる重要な方法の1つは「共通点と差異」（同じここと違うこと）に注目することです。

違いを明確にし、対象をグループ分けし、そのグループの中で共通点を探す。
たとえば、A～Dの対象物の共通点がすぐに見つからない。そういった場合、 A～Dの対象物をグループ分けできる差異を見つけ、
そのグループの中で共通点を考えます。

こういった方法論は、たしかに日々の実験や試行錯誤で身につくものですが、まずフレームとして学習する機会を持つべきではないでしょうか。

灘中より。無粋な手法の中にも答えがあります。

下の2つの図は、各面に1から6までの数が書かれた立方体の展開図である。それぞれの立方体の1つの頂点に集まる3つの面に書かれた数の和を考える。この和のうち最大のものは（図1）では15、（図2）ではいくつか。
　　　　　　　　　

(灘中）

そもそも頂点の数は・・・。

組み立てた状態を考えると下の図のようになります。

頂点は8こなので、8つの頂点についてすべて調べてみます。
すると
4＋2＋3＝9、
4＋2＋6＝12、
4＋1＋3＝8、
4＋6＋1＝11、
5＋1＋3＝9、
5＋3＋2＝10、
5＋2＋6＝13、
5＋6＋1＝12
となり、最大のものは13。

答え：13

「最大」を生み出すメカニズムについて検討する姿勢はとても大切です。

しかし、場合の数など組み合わせについて考える問題においては、
そもそも検討すべきパターンがいくつぐらいあるのかについて概算してみる姿勢が大切です。

本問では実は8つの頂点についてしらみつぶしに調べればすぐに終わります。

～今回の問題より導かれる出題校からのメッセージ～
作業量の見通しを常に検討する姿勢が大切

「しらみつぶし」は、上位の生徒にとって、そして指導者にとってあまり洗練されたものではありません。

しかし、状況に応じて「最善」である場合もあるのです。

例えばさいころ問題では2個のさいころであれば36通りの組み合わせしかありませんから、
すべて調べてもたいした時間はかからない上に、確実です。

反対に4個ですと、1296通りですから、何か法則を見つけなければ太刀打ちできません。

解法を決めてかからず、解いている最中でも常に別の道筋を検討する姿勢は、
本校が生徒に期待する学問に対する姿勢に他ならないといえます。

灘中より。割り算の筆算ができますか？

整数（A）を整数（B）で割ると、商が32で余りが10であった。さらに割り算をつづけて小数第3位まで求めると商は32.322となり、余りが出た。（A）（B）に入る数を求めなさい。

(灘中）

「割り算を続ける」という作業を筆算で確認してみてください。

商が32、余りが10の状態からさらに割り算を続けるというのは、
余りの10を整数（B）で割るということです。

その商が32に続く小数部分となります。

つまり
10÷B＝0.322・・・である。
よってB＝31.05・・・・からB＝31
ゆえにA＝32×31＋10＝1002

答え：A：1002　　B：31

計算や筆算の仕組みを理解し、きちんとイメージできるかどうかが問われています。

50分で15問ですから、本問に割くことのできる時間はだいたい2分程度です。

普段から定石問題についても深い考察をしていくことが大切です。

本問は割り算の筆算の手順についてイメージできればとても簡単な問題です。

「割り算を続ける」とは、「余りを割り続ける」という作業なのです。

～今回の問題より導かれる出題校からのメッセージ～
計算技術の仕組みと意味の理解が大切

灘中ではよく出題されるポイントとして、 筆算や各種の法則などを
使うことには慣れていてもその仕組みや意味をきちんと説明すること
が難しい知識を必要とされるものがあります。

かつては壮大な虫食い算などが主流でしたが、最近は本問のような
計算の経過を文章で与えるという形式が好まれています。

本問も普通の割り算を文章化しただけなのですが、とたんに混乱して
しまう生徒も少なくありません。

一度低学年にするような形で説明する機会を持たせると、高学年
でも様々な計算技術の中に気付きを得られると思います。

それらの気付きなしでは、本校の1日目を高得点で乗り切ることは
不可能です。当たり前の知識に関しても表面的な理解に留まらず、
きちんと検討する。　1日目の問題はそういった付け焼刃では身に
付かない勉強への基本姿勢を測定する問題だといえるでしょう。 。

麻布中より。求められているのは直感力や発想力なのでしょうか。

高いところから静かに小石を落とすと，小石はどのように落ちていくでしょう。

　16世紀から17世紀に活躍したイタリアの学者ガリレオ・ガリレイは，この「落体の運動」について初めてくわしい実験を行い，その法則を明らかにしました。そのころの学者はみんな「重い物体のほうが軽い物体より速く落ちる」と考えていました（図1）。ガリレオは「重い物体も軽い物体も同じ高さから落とすと，同じ速さで落ちて同時に地面に落下する。」と主張して，ピサの斜塔の上から大小2つの鉄の砲弾を落とす実験をしてみせたという話が伝わっています。

　ガリレオは実験だけでなく，(1)同じ高さから物体を落としたとき，重い物体のほうが，軽い物体より速く落ちると仮定すると，矛盾が生じることを示しました。以下この矛盾について考えます。

　大きく重い鉄の球A，小さく軽い鉄の球B，そして，A，Bと大きさと重さがそれぞれ等しい2つの鉄の球を接着剤でくっつけたものをCとし（図），それらを同時に同じ高さから落とすとどうなるか考えてみます。

まずCをひとかたまりのものと考えます。

問1　下線部(1)の仮定が正しいとすると，A，B，Cはどの順で落下することになりますか。下のア～オの中から選びなさい。
ア．A，B，Cの順に落下する。
イ．A，C，Bの順に落下する。
ウ．C，A，Bの順に落下する。
エ．AとCが同時に落下し，Bが後で落下する。
オ．Aが先に落ち，後でBとCが同時に落下する。

　つぎにCを重い球の部分と，軽い球の部分の2つに分けて考えると，（2）(1)の仮定から，重い球の部分は速く落ちようとし，軽い球の部分はおそく落ちようとして，たがいに引き合うことになります。

問2　下線部(2)から考えると，A，B，Cはどの順で落下することになりますか。問1のア～オの中から選びなさい。

問3　問1，問2から考えると，「重いものが軽いものより速く落ちる」という仮定はまちがっていることになります。その理由を説明しなさい。

(麻布中・抜粋）

知識を当てはめようとせず、これまで使ったことのある「考え方」を当てはめてください。

問1　ウ
問2　イ
問3　「重いものが軽いものより早く落ちる」とすると、その仮定にもとづいてCを一つのかたまりと考えるときと、CをAとBの二つの部分で考えたときで、本来同一となるはずの実験結果が異なる。これは明らかにおかしい。よって、最初の仮定が誤っていたということが言える。

問2　大きい球の重さをG、小さい球の重さをgとする。　G＞g。

AとCをくらべる。C大きな球はCの小さな球に引っ張られるためAの球よりも遅く落ちる。　

BとCを比べる。Cの小さな球はCの大きな球に引っ張られるためBの球よりも速く落ちる。

これより、Cの球は、Bよりも速く落下し、Aよりも遅く落下する。

問3　<<とある事象が間違っていることを説明する方法>>
　　　
とある事象が正しいとして、話を続けると明らかな矛盾や、あきらかな事実との相違があることを説明。
⇒よって、とある事実が正しいという仮定がまちがっている。

～今回の問題より導かれる出題校からのメッセージ～
思考方法で分類された学習方法を確立してほしい

麻布中学や武蔵中学でよくあるタイプの問題ですが、教科書に掲載されているような問題とは全く違い、おそらく同様の問題を解いたことのある受験生はいないと思います。

見たところ、勘のいい小学校低学年・中学年の生徒でも正解できるのではないかとすら思われます。
（実際、教室では3年生で複数人正解の記述ができていました。）

麻布中は、これまでの受験勉強の内容ではなく、ひらめきや直感力、勘の良さを持った生徒を欲しているということでしょうか。

もちろんそんなことはありません。

この問題などは典型的に「論理の積み重ね」を行う訓練をしてきたか、仮設を持って話を進める訓練をしてきたか、そして、「説明する」といった作法を体系的に学習してきたか、を試している問題です。

たしかに教科書や問題集の章立て構成に従い、学習塾のカリキュラム消化につき合わされっぱなしの生徒にとってこの種の問題は大変やっかいです。

教科書の章立てでの勉強方法は確かに便利で分かりやすいです。しかし、「今日は滑車の章だから滑車の知識をつかって問題を解く」というような学習パターンが身についてしまうと、上のような問題に対して対応できなくなることがあります。

日々の学習の中で、自分が使っている思考方法をたえず意識する。
「この問題は典型的な推論問題だな」「この問題はいつもの『間違っていることを証明』するタイプだな」
e.t.c

与えられた知識分野別の章立てカリキュラムだけでなく
「思考法で分類された学習方法」を自分で実践すべきです。

駒場東邦中より。複雑な立体切断を基本定理に落とし込みます。

下の図のように1辺の長さ2ｃｍの立方体を4個はり合わせてできた立体を考えます。この立体を3つの頂点Ａ、Ｂ、Ｃを通る平面で切断しました。

（１） 上の図に切り口の図形を書き入れなさい。

（２）（３）省略

(駒場東邦中)

切り口のラインの中で、明らかなものからひとつずつ描いて行きましょう。

切断面は図のとおり

立体図形を平面で切断したときにできる 断面の切り口を求める問題では
基本のルールをしっかりと追っていくことが重要になります。

（基本ルール１）
切断面は必ず切断するように指定された点を通る
当たり前のように思えますが、一番大事なルールです。
今回の場合、これでまず頂点Aと頂点Bを結ぶ直線が結べます。

また、

（基本ルール２）
切断面は必ず連続している
も一見当然のように見えますが大切なルールです。

（基本ルール３）
向かい合う平行な平面の上を通る切り口は平行である
このルール２を使うと、ルール１と合わせて頂点Cから線分ABと平行につながる
切り口を描くことができます。

（基本ルール４）
切断する平面上の各点を結ぶ線上に、切断される立体の外壁が重なれば
そこは切り口である

ここまでくると、すこし立体的な想像力が必要となってきます。
ただ、最初の３つのルールに従って条件整理ができていれば
作業はずっと間楽になっているはずです。

ここで三角形ABCを考えてみると頂点Aと頂点Bから
斜めにのびる線分が引けます。
ここさえ書くことができれば残りの線は すべて最初の３つのルールから描くことができます。

～今回の問題より導かれる出題校からのメッセージ～
想像力の不足は論理の積み重ねで補うことが大切

算数の図形問題、とくに立体図形の問題はひらめきや立体的なイメージ力 が大切だと思われがちです。

しかし、今回の問題のように基本のルールをしっかりと守って きちんと条件整理をすることで 一見トリッキーに見える問題でもずっと簡単に解くことができます。

どんな算数の問題でも大事なのは基本的なルール。
一見難しそうに思える問題でもしっかりと条件を整理していけば 簡単な基本の組み合わせに分割できることを理解しましょう。

灘中より。非常に短い問題文を整理する国語力が問われます。

ある5桁の整数があります。この整数には、数字0がA個、数字1がB個、数字2がC個、数字3がD個、数字4がE個使われていて、これ以外の数字は使われていません。また、この5桁の整数は一万の位から順にABCDEとなっています。ABCDEの中には同じ数字があってもよく、BCDEは0であってもよいものとします。この5桁の整数を求めてください。

(灘中）

紛らわしいかたちで与えられている2つの条件を整理しましょう。

A、B、C、D、Eは、それぞれ5桁の整数の中で、0、1、2、3、4の数字が使われている個数ですから、
A＋B＋C＋D＋E=5です。

また、Aは5桁の数の先頭なので1以上です。
これは、Aは数字0の個数も表しているので、同時に数字0も1個以上あることを意味します。

0が1個以上あるということより、1、2、3、4の数字はあわせて4個以下しか使われていません。
さらに、その使われているA、B、C、D、Eの合計は5と決まっているので5つの数字の組み合わせは、

（0、0、0、1、4）（0、0、0、2、3）（0、0、1、1、3）（0、0、1、2、2）（0、1、1、1、2）

の5通りしかありません。

この中（0、0、0、1、4）は、「4」に着目すると、4つ使われている数字は明らかにないので不適。
同様に（0、0、0、2、3）も「2」に着目すると不適、
（0、0、1、1、3）も「3」に着目して不適、
（0、1、1、1、2）も「2」に着目して不適。

よって（0、0、1、2、2）を問題文の条件どおりに並び替えた21200が求める数になります。

答え：21200

短い問題文ですが、題意を非常にとらえにくくなっています。

「5桁の数ABCDEの各位の数A、B、C、D、Eは、
同時にA、B、C、D、Eの中にある0、1、2、3、4の数字の個数を表している。」

という分割して考えにくい2つの条件を整理して、チェックする姿勢にたどり着けるかどうかが分かれ目になっています。

後半の条件は数式化しやすく（A+B+C+D+E＝5）、
それを土台にして前半部分の突破口である「Aは1以上、
同時に0は1個以上」から手をつけていきます。

～今回の問題より導かれる出題校からのメッセージ～
日本語で書かれた見にくい条件文をきちんと理解し、整理することが必要です。

灘中の入試では、非常に短い問題文の中に隠されている複数の条件を、「使える形」で瞬時に整理する力が問われます。

コツは、どの日本語を既に使ったかどうかを明確にしておくことです。

本問では、ほとんどの生徒が、まずA+B+C+D+E＝5という条件を見つけることになるとおもいます。
ここで問題文を離れ、書き出しや当てはめを始める生徒がよく見られますが、
「問題文の5桁の数は一万の位から順にABCDE」を処理できていないのです。

一つ一つの日本語を精査する読解力。

算数の短問の中においても重要となるのはやはり国語力です。

桐朋中より。基礎知識は複合化できてこそ理解したといえます。

aグラムのアルミニウムを試験管に入れ、これにbグラムの塩酸を入れたところ、アルミニウムがすべてとけました。とけた後の水溶液の重さをはかったところ、cグラムでした。この水溶液を加熱して、水を蒸発させていくと、にごりはじめ、水が無くなるとdグラムの個体Eが得られました。

問1
以下の量の組み合わせで、右に記した重さが大きい場合は、「右」、左に記した重さが大きい場合は「左」、等しい場合は「同」と書きなさい。
(1)（aグラム+bグラム、ｃグラム）
(2)（ｃグラム、dグラム）
(3)（aグラム、dグラム）

問2
個体Eをdグラム取り、これがちょうどとけるまで水を加えました。ここで生じる水溶液の重さがｆグラムとすると、fとcではどちらが大きいですか。次のア～エから１つ選び、記号で答えなさい。
ア.　fの方が大きい
イ.　cの方が大きい
ウ.　ｆとｃは等しい
エ.　これだけでは判断できない

(桐朋中・抜粋）

受験生ならだれでも知っている反応です。現象を丸暗記せずに式のかたちで理解できていますか。

問1　(1)左　(2)左　(3）右
問2　イ

下の（化学）式が書けるかどうかですべては決まります。
書けない人は、どういった反応が起きているのかという理解をおこたり、教科書に書いてある結果のみを暗記し
理解したつもりになっている人です。

そして大事な基礎知識が反応の前後で質量の変化はありません。つまり上記反応の左辺と右辺の質量は等しくなります。
また、塩酸水溶液が、塩酸が水に溶けたものだという基礎知識がきちんと応用できるかどうかも確認すべき点ですね。

問1
(1)上式を参考にするまでもなく、逃げていった水素の分だけcが軽くなります。
(2)上式参照
(3)塩酸とアルミニウムの反応は、大雑把に言えば、「塩酸が2つに分解し、一つは水素として気体として空気中に出ていき、もう一方はアルミニウムと化合する」反応です。アルミニウム自体は複数に分かれてはいません。

問2
「にごりはじめる」という状態がどういう状態であるかに着目できるかどうかが鍵となります。
にごりはじめる→飽和水溶液となるということであり、これがつまりｆの状態です。

cグラムから水をとりのぞいて、ｆグラム　になるのですから ｃ＞ｆです。

～今回の問題より導かれる出題校からのメッセージ～
知識の複合化ができるまで理解を掘り下げる

この問題であつかっている内容は、我々が普段「塩酸」として扱うものが本来「塩酸水溶液」であることの理解であったり、
塩酸とアルミニウムの反応であったり、飽和水溶液の知識であったり、
それぞれは基礎中の基礎といった知識です。

が、これらがうまく複合され出題されると、その知識理解の甘さが露呈するものです。

「基礎問題はわかるのに応用になるとどうも」 といった声の大半はここにあるのですが、
こういった場合、基礎問題も本来分かっていないのです。本当に「理解」したというレベルまでいっていないのです。

この問題が教えてくれることの一つは、
「基礎として紹介される事象でも、それを応用するには想像を超える努力が必要であること」であり、
「簡単に『理解した』と納得しない癖をつける大切さ」です。

そして、保護者・指導者は、苦労をいとわず、そして決められたカリキュラムを消化することにとらわれることなく、
教科書レベルの事象の深堀の重要性を生徒に今一度説くべきです。
本当に生徒は、基礎レベルの知識を理解しているのか。疑ってかかることも時には必要です。

東邦大学付属東邦中より。概算と精査の組み合わせです。

となるように、□の中に1から9までの異なる整数をあてはめます。このとき　ア、イ、ウ　の合計はいくつになりますか。

ア、イ、ウが同じ数だとしたらいくつになるでしょうか。

ア、イ、ウが同じ数だとしたら３です。

つまりア、イ、ウが異なる場合、すべて3以上の数にすると合計が1に満たないことになります。
（例えば1/3+1/4+1/5は1に満たない。）

よって、ア、イ、ウのうち一番小さい数は2であることがわかります。これをアとします。

よって残りの2つの分数の和は1/2となります。

ここで、先程と同様にイ、ウが同じ数だとすると4となります。
つまりイ、ウが異なる場合、ともに4以上の数にすると合計が1/2に満たないことになります。
（例えば1/4+1/5は1/2に満たない。）

よってイ、ウのうち小さいほうの数は3となります。
これをイとすると、ウは6になります。
3つの数の合計は2+3+6=11

答え：11

初見だとしたらかなりの難問です。

「同じ数だとしたら」すべてが3となること。
3つ異なる数ですから小さい順にア＜イ＜ウとなること。

そこから最初の2を見つけることが突破口です。
与えられた条件をひとまず無視して計算をして、そこから条件にあわせて微調整していくという手法はつるかめ算などにも共通する技術です。
まずは「概算」で見通しを立てる。
方程式の通用しにくい中学入試ではとても大切なステップです。

～今回の問題より導かれる出題校からのメッセージ～
概算と精査のバランスが大切

本問のように一気に答えを算出する方法がない問題は、中学入試では多数出題されています。

ひたすら書き出していくしかなかったりするものもすくなくありません。

そんななかでも、書き出しの量を減らす工夫はとても大切です。

大雑把に答えの周辺にあたりをつけてみることで、明らかに不要な部分を省略することができます。
また、とりあえずの計算をしてみることで、答えが大体どれくらいの範囲におさまりそうなのかということも把握することができます。

「とりあえずやってみる。」

闇雲な第一歩がゴールへ近づく近道となります。

栄光学園中より。与えられた条件の意味を掘り下げる力が問われます。

20名のあるクラスで次のような方法で席替えを行いました。
（１）くじで２人１組のペアを１０組つくる。
（２）そのペアになった２人の間で席を入れ替える。
（３）（１）、（２）をもう一度くりかえす。
席替えをした後も席替えをする前と同じ席に座っている生徒が１１名になることはありえません。その理由を答えてください。

(栄光学園中）

ありえないとされる「１１」という数字の特性に着目してみましょう。

１回目の（１）（２）の席替えで必ず全員が自分の席を離れることになる。
２回目の席替えを考える。

ある人が元の席に戻るためには、
１回目終了時点で元の自分の席に座っている人、
つまり１回目の席替えでペアになった人と２回目の席替えでもペアにならなくてはいけない。

このとき、相手も元の席に戻ることになる。
つまり、２回目の席替えである人が元の席に戻るということは、
１回目の席替えの相手も元の席に戻ることを意味する。
よって２回目の席替え終了時点で、
元の席に戻る人数は必ず２人の倍数になるので問題の「１１人」は該当しない。

「どんな方法によっても」１１人がありえないことを説明するというのは、コツが必要です。

A）すべての方法を試して１１人という結果がないことを示す。
B）「１１人」という個別の数字ではなく、
「奇数はありえない」「過半数はありえない」など「１１」のもつ特性に着目して証明の目標を緩くして論証する。

のどちらかです。
A）を稚拙だと決め付けてはいけません。高々数十通りの可能性であればそのほうが完結な場合もあります。
今回は、B)です。ほとんどの受験生が２回の席替えの場合の数はかなり多いことを容易に想像すると思いますので、
B)の方針で検討したことかと思います。

「すべて」「かなら」の証明にはある程度の習熟が必要ですので、
身の回りや通常のディスカッション・説明の機会を活かしていくことが大切です。

～今回の問題より導かれる出題校からのメッセージ～
論点を適宜変形していく力が大切

証明は中学生の範囲ですが、
論点の整理と論証の方向付けの能力というものは小学生に対しても十分に問うことの出来る分野です。

本問で問われているのは
「とあること」を証明するということは、何を意味するのか。
ということを掘り下げる力です。

直接は説明できなくても、同じことを意味するものを見つけ出し、
そちらの説明へと方針を転換する。

身近なものでは対偶をつかった証明など「間接的な」証明能力が問われる場面は少なくありません。

与えられた条件を様々な角度から検討し、知識を動員して同値なものに確実に変形していく力は、
未知の問題を身近な問題に引き寄せる能力としてまさに応用力そのものと定義できます。

本問はその力を測る良問ですし、同じ形式を出題し続ける本校が最も大切だと考える能力であることを宣言している問題ともいえます。

開成中より。問題文を読み解く力。グラフの二段階読解。

あきら君は，ミツバチに興味を持ったので，ミツバチについてよりくわしく調べてみることにしました。ミツバチは，ミツを探しにいくときには胃の中はほとんどからの状態で巣から飛び出していきます。ミツバチが花のミツをすうと，胃にミツをため，それを巣に持ち帰って巣にたくわえていきます。屋外で飼われているミツバチについて，まず巣の中にミツを用意して，ミツをすわせたとき（これを「巣内」とします）の重さを調べました。次に，巣から出ていくとき（「出巣時」とします）の重さと，ミツを集めて巣にもどってきたとき（「帰巣時」とします）の重さを調べました。このときの重さの変化は，すべてすったミツによるものだと考えられます。それについて100匹ずつのミツバチの重さを調べ、どの重さのミツバチが何匹いるかを調べたものをグラフにまとめました。

問1　ミツバチの胃の中には、平均的に何mgのミツをためることができると考えられますか。もっとも適切な数値を、次のア～オの中から1つ選び、記号で答えなさい。

ア　30mg　イ　40mg　ウ　70mg　エ　120mg　オ　150mg

問2　ミツを見つけるのに成功したミツバチは、1匹あたり平均して、どのくらいのミツをすってもどってきたと考えられますか。もっとも適切な数値を、次のア～オの中から１つ選び、記号で答えなさい。

ア　30mg　イ　40mg　ウ　70mg　エ　120mg　オ　150mg

(開成中・抜粋）

帰巣時のグラフの山がきれいに二つに分かれていることに着目します。

問1　ウ（70mg）　
問2　イ（40mg）

問1
まず、たとえば、100mgのミツバチが二匹、80グラムのミツバチが1匹いたら、
平均の1匹の体重は、（100mg×2匹　+　70mg×1匹）÷3匹＝90mg　となる。
この平均の考え方を理解していることが出発点となります。
巣内の状態では満腹であり、出巣時には、胃の中のミツは空になっている（だから、巣から出てミツをとりにいく）と、考えると、
（ミツバチが胃に蓄えられるミツの量）＝（ミツバチの巣内の体重）－（ミツバチの出巣時の体重）　で求められる。
ミツバチの巣内の体重＝（140mg×10匹　+　150mg×80匹　+　160mg×10匹）÷100匹＝150mg
ミツバチの出巣時の体重＝（70mg×20匹　+　80mg×60匹　+　90mg×20匹）÷100＝80mg
となり、この差の70mgが解答となる。

問2
帰巣時の体重のグラフを見ると山がきれいに二つできていることに気がつきます。
このグラフのカタチをみて「ん？なぜだ？」と立ち止まれるかどうかがこの問題を解けるかどうかの分かれ道となります。
ここで頭に「？」が浮かべば、二つの山のうち左側は「ミツを取ってくることができなかったハチだ」と考えることができます。
なので、グラフ右側の山のミツバチだけを考えます。
（ここは厳密に考えるとまだ考察ポイントがあります。後述。）
（ミツバチが取ってこられるミツの量）＝（ミツバチの帰巣時の体重）－（ミツバチの出巣時の体重）で求められる。
ミツバチの帰巣時の体重＝（100mg×1匹+110mg×7匹+120mg×24匹+130mg×7匹+140mg×1匹）÷40匹＝120mg
ミツバチの出巣時の体重＝80mg　←問1より
となり、この差の40mgが解答となる。
-------------------------------------------------------------------

＊上記の「山の左側はミツをとってこられなかったハチだ」と仮定し、解答を得ていますが、厳密にはそうでない場合もありえます。

たとえば、出巣時70mgが20匹おり、このうち、12匹がミツをとれずに帰ってきて、8匹が80mgになって帰ってきた。
出巣時80mgが60匹おり、このうち、28匹がミツをとれずに帰ってきて、12匹が90mgになり、1匹が100mgになり、7匹が110mgになり、12匹が120mgになって帰ってきた。
出巣時90mgが20匹おり、このうち、12匹が120mgとなり、7匹が130mgとなり、1匹が140mgとなって帰ってきた。
という場合を想定すると、与えられたグラフと同様のものが描けます。この場合、問2と同じ解答は導くことはできません。
つまり、左側の山が「ミツをとってこなかったハチ」ではない場合もあり得、その場合この問題は解答を得られません。
グラフをみて、きれいな二つの山から考察し、仮定を立てる力を試す問題であるという点で良問ではありますが、「そうはならない可能性」がある点に問題文でなにかしら触れるべきであるという思いはぬぐえません。

～今回の問題より導かれる出題校からのメッセージ～
グラフの裏側にあるメッセージを探る

解説でも触れたように、本問の鍵は、グラフの読み取りです。
たんなる読み取りではなく、グラフが語る事象を読み解く能力です。

グラフをみて、そのグラフが何を語るかは数段階あります。

たとえば、人口増減のグラフをみて、
「日本の人口は減っている」ということを読むことが第一段階。
「このままだと、労働力が不足するかもしれない」という仮説を含んだ思考を創るのが第2段階です。

グラフを正確によみとることはもちろん大事ですが、
その先にある事象を考えることが求められています。