学習塾ロジム　今週の1問by 学習塾ロジム

学習院女子中より。物事を説明する基本技をここで一つ習得してください。

月を注意 して観察すると、私たちでも、地球上にいながら、下の表のことがらを知ることができます。どのようなことから、それがわかりますか。それぞれについて、説明しなさい。
(1)月は、夜空に明るくかがやいているときでも月の内部からは光を出していない。
(2)月がかがやいて見えるのは、太陽の光を反射しているからである。
(3)月は満月のとき、平らな円板のように見えるが、実際の月の形は球形である。
(4)地球から見ると、月は太陽とほぼ同じ大きさに見えるが、月は太陽より私たちに近いところにある。
(5)月のまわりには、ほとんど大気がない。

「Aでない」と仮定して、その話が確実に間違いならば、「Aである」といえます。

(1) 月が満ち欠けをすることから。
（もしも月が自分で光を発しているならば、月は満ち欠けせずに、（自ら光を発する太陽のように）いつでも満月状に輝いている。しかし、実際には月は満ち欠 けをすることから、月は自ら光を出してはいない。）

(2)月食が起こるから。
（（月-地球-太陽）と並んだときに、月食が起きることから。）

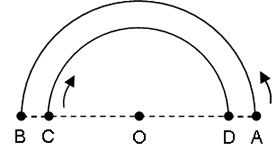
(3)月の中央部のクレーターは円形なのに、端に行くにしたがってつぶれた形（だ円形）になっているから。

(4)日食がおこることから。
（もし、月が太陽と同距離、もしくは太陽より遠い場合、地球と太陽の間に月が入ることでおきる日食は起きない。が、実際には、月の影が影をつくり日食は起 きため、月は太陽より地球に近いことがわかる）

（5）光の屈折が観測されないから。　／　月に大気が存在するとしたら、月が他の遠い（小さい）星を隠すときに、まず月の大気が星を隠すため、はじめ星が ぼやけ始め、その後、月本体によってその星が隠れるはずである。しかし、月が星を隠す際は、段階的に星が暗くなることはなく、一瞬で消えるため。

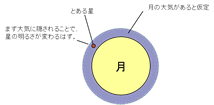
（3）
授業の際、
「たまたまはじにあるクレーターがだ円形で中央にあるクレーターが正円に近いだけではないか」
という意見もでました。
とある一つのクレーターを観察しつづけ、このクレーターが中央にあるときと、はじにあるときで形がかわることまで言えば、この疑問は解決されます。

-------------------------
物事を説明・証明するときの大事なテクニック

「Aである」ことを証明・説明するために、

「Aでないとしたら」と仮定し、その矛盾を示し、

したがって、

「Aである」と結論する。
--------------------------
中学以降「背理法」として紹介される方法論ですが、もちろんみなさんも
日常的に行っている論理展開です。

何かを説明する。
訓練を積んでいないとなかなか難しいはずです。
上記の説明テクニックは中学入試でも活用箇所が大変多いですので、
覚えておいて損はないはずです。

～今回の問題から導かれる出題校からのメッセージ～

「あたりまえ」の事実を言葉で説明できる能力 をもって入学してほしい

算 数の公式や定理・公理、
理科の常識をあらためて説明することは、想像以上に骨が折れる作業です。

現状教育の現場では、とあるルールを与え、それを応用する能力が重要視されているといえます。
みなさんが慣れ親しんでいる試験はまさにこの分野でしょう。

しかし、その反面、ルール自体や、定義・定理、身の回りの常識の理解が
おろそかになっている生徒を多数生み出しています。

本問は、
・　とりあえず公式や常識をマスターしてそれをつかえればいい
・　説明は苦手。塾や学校で教わった説明を覚えておこう

という生徒が増えた現状に警笛を鳴らし、改めて定義や常識を説明することの重要性を
教えてくれる良問といえるのではないでしょうか。

近年上位校と呼ばれる学校で「定義の理解確認。常識とされる事柄の論理的説明」
問題が多く出題されています。
この機会に「何気なく前提としている常識」を見直してみてはいかがでしょうか。
（塾や学校の先生の説明を聞きっぱなしにしたり、小学生の学習範囲かどうかを気にするのではなく、
意地悪いほどに、「そもそもなぜ。なぜなぜ。」と質問してみるべきです。）

城北中より。「身の回りの算数」に向き合う姿勢が大切です。

ある月の月曜日の日にちの数字の和が６６のとき、この月の2日は何曜日でしょうか。

（城北中）　　　　　　

同じ曜日の日付には、大きな制限が存在します。

同じ曜日の日付は、前の週＋7日となっています。
つまり
1週目をX日とすると
2週目：X＋７
3週目：X＋７＋７
4週目：X＋7＋7＋７
5週目：X＋7＋7＋7＋7
となっているのです。
ここで、Xが何日であれ、5週目まであるとすると、そこに含まれる「７」の数は10個となり、
日付の和は「X×５＋70」、つまりXが1日でも日付の合計は75日になるのです。
今回、考える月曜日の日付の和は66なので、この月に月曜日は4日しかなかったことがわかります。
よって4週目までの日付の合計の式より
X×４＋７×６＝６６
となり、Xつまり1週目の日付は6日です。
6日が月曜日の月では、2日は木曜日となります。

答え：木曜日

今週の一問でも何度か取り上げた
「問題文では明記されていないあたりまえの制限を活用する。」
問題です。

今回の「日付」は、その中でもよく出題される題材です。
初見の場合、「日付の合計だけで曜日が決まってくるのか。」という壁にぶつかります。

通常の塾のカリキュラムでは、連続する整数の和など類題も数多く学ぶことになりますが
このタイプの制限は、見た目を変えて出題しやすくまた、問題文の中に埋もれて見にくくなっています。

整数倍や人数と比などの形で抽象化してまとめておかなければ、
なかなか気づけるほどの認識力は身につきません。
解答を読むと、「気づかなかった」というレベルで済ましてしまいがちですが、
日ごろのまとめる作法が問われる問題です。

～今回の問題から導かれる出題校からのメッセージ～
「身の回りの算数」に向き合う姿勢が大切

本問に一度取り組んでおけば、類題は問題なく解けることになります。

しかし、本問を通して学ばなければならないのは、
「問題文の日本語に隠された数学的な意味を探りながら読む習慣」
の大切さです。

算数や数学を使ってとくべき問題は、身の回りにたくさんあります。
しかし、その問題は数式によっては与えられていません。

「算数として考えると・・・、数学的に考えると・・・」という普段からの問いかけだけが、
日本語として与えられる条件と数式を行ったりきたりする能力を育みます。

カレンダーという身近なものに含まれる算数を探求させる本問は、
問題を離れた世界で数学的思考の適用力を測る良問です。

浦和明の星中より。基本問題の目先を上手に変えた問題です。

下の図のように、点Oを中心とする半径60mと半径40mの2つの半円があります。
明子さんは、点Aから出発して半径60mの半円の円周上を点Aから点Bまで往復し、
星子さんは点Cから出発して半径40mの円周上を点Cから点Dまで往復します。

2人の速さは同じで、星子さんが点Cから点Dまでの片道を移動するのに50秒かかります。
2人が同時に出発するとき、次の問いに答えなさい。

（１）初めて点Oと2人の位置が一直線上に並ぶのは出発してから何秒後ですか。
（２）2度目に点Oと2人の位置が一直線上に並ぶのは出発してから何秒後ですか。

　
（浦和明の星中）　　　　　　　　　　　

「一直線上」をしっかりと意識すると、見慣れた問題に落としこめます。

（１）
星子さんの回転する角度は180÷50＝3.6度/秒
明子さんの回転する速度は同じだが、
より半径の大きい半円を回っているので、同じ時間で回転する
角度は小さくなる。

半径の比が60：40＝3：2であるので、同じ長さの弧に対する中心角は2：3となる。

よって回転する角度は3.6×2/3＝2.4度/秒
一直線上になるということは、つまり二人合わせて180度回転した時であるから、
180÷（3.6÷2.4）＝30秒後
答え：30秒後　

（２）
2度目に一直線上になるということは、2人の回転した合計角度が540度になるときです。
540÷（3.6÷2.4）＝90秒後
答え：90秒後

時計の針の問題以外で回転 角の速さを考える問題に取り組んだことのある生徒はほとんどいなかったのではないでしょうか。

当日、後回しにした生徒も多かったようですが、時計を想像すればかなりの易問です。

ポイントは、一直線の 状態をきちんと記入してみること。

そして、その状態を求める上での必要条件を整理することです。
一直線上について検討する作業を通じて、回転角を活用することにたどり着きます。

（２）は意外と気づかないまま受験を迎えてしまう生徒が多いのですが、旅人算の隠れた基本です。

「距離がわからなくても、ある区間ABにおいてA、Bから向かい合って出発し
X分後に出会った二人が2回目に出会うのは３X分後。」

絵を描いて二人が進む距離を考えるとわかります。

～今 回の問題から導かれる出題校からのメッセージ～
普段から問題に含まれている重要項目を確認することが大切

浦和明の星中の算数は、入学後の数学に耐えられる生徒を集めようという意志が
強く感じられる内容になっています。

図形の性質を活かして式を立てるなど、
単純に図形センスを測定する問題と括ることのできない内容になっています。

ポイントは、図形の性質について深い理解をしておくこと、求積の公式についてその成り立ちをしっかりと理解しておくことです。

「正方形だから・・・」だけでなく、
「・・・・だから正方形」「正方形とは・・・」

などの形で知識を再確認しておくことが有益でしょう。

本問は、角速度について正しくイメージする基本的な力を問う問題です。
時計の問題との類似性を見抜けないのは、

「角度と速度の問題」がいつのまにか「時計の針の出会う問題」

という表面的な形でインプットされてしまっているからです。（実際の出題も多いのですが。）

本質的な部分をくずさず、目先を変えてくるという、
普段から、一段深いレベルで問題を分析する習慣の大切さを問いかけてくる良問です。

開成中理科入試より。理科の問題と考えずに、情報整理能力を問う問題だと考えるべきです。

　植物は光が当たると二酸化炭素を吸収し、酸素を放出して、でんぷんをつくります（これを光合成といいます）。その一方で、私たちと同じように呼吸も行っ ています。二酸化炭素と酸素だけに注目してみると、次のようになります。

今、話を簡単にするために、次のようにします（本当は少し違います）。

・光合成で吸収される二酸化炭素と、放出される酸素の体積は同じ。
・呼吸で吸収される酸素と、放出される二酸化炭素の体積は同じ。
・光合成の行われ方は、光が強くなったり、温度が高くなれば活発になるが、呼吸の方は、温度が高くなると活発になるが、光の強さには左右されない。
う
　　これらをもとに、次の実験を行いました。

［実験］
右の図のように、とう明なプラスチックの箱を 6つ用意し、それぞれの箱の中に、同じ大きさのヘチマのなえを入れます。
　（各箱内のヘチマは、条件が同じなら、同じ割合で光合成と呼吸
　　を行うものとします。）
　
条件として、
光の強さは3種類（強い光…A、弱い光…B、暗黒…C）、
温度は2種類（30℃…a、20℃…b）　　　　とし、

これらを組み合わせて右の表のように6種類の 箱（イ～ヘ）をつくりました。

　　なお、強い光なら、光合成での二酸化炭素や酸素の出入りの方が、呼吸での出入り よりもはるかに多量です。

実験を続けて3時間後に、箱内の二酸化炭素と酸素の割合を、それぞれ気体検知管で調べました。その結果を考えて次の各問いに答えなさい。答えは箱の記号 イ ～ヘで答え、同じものを何度選んでもかまいません。また、これまでに述べた条件だけからでは1つにしぼれない場合は、その可能性があるものすべてを選びなさい。

　間1　30℃のときの呼吸による変化だけがあらわれたのはどれですか。
　問2　酸素の割合が最も多くなったのはどれですか。
　間3　二酸化炭素の割合が最も多くなったのはどれですか。
　間4　二酸化炭素と酸素の割合が、実験開始前とほとんど変わらなかったのはどれですか。

とある結果に対する原因を特定、整理します。

問 1　ハ
問2　イ、　ニ
問3　ハ
問4　ロ、　ホ

「同時に複数のことを考える」
小学生ならずとも多くの人が苦手とする行動ではないでしょうか。
しかも、その複数が、互いに影響していればなおさらですね。

光を強くすると、光合成を活発にして酸素を増やせるが、同時に呼吸も活発になるので、酸素は減る。
違う方向の反応が同時に起きるわけです。

こういった問題を考えるときは、

・問題をよく読む　→　条件整理の準備を徹底する
・ドライバー（結果を生む要素）に視点を置く

が必勝法です。
まず、問題文をよく読んだ上で、
下記のような表を書きます。こういった表が書ければ、話はずっと簡単になります。

問１　
30度において呼吸だけ　→　光合成しない　→　30度で光がない　→　ハ
問2　
上図より温度をあげることにより、酸素と二酸化炭素の増減は相殺されるため、温度の差を無視することができる。よって、光を強くしている　イとニが解
問3
二酸化炭素の割合が多い→　光合成を出来るだけしなく、呼吸を盛んにしている
光合成をゼロにしても呼吸はできるため、光をゼロにし、呼吸を盛んにするために温度を上げる。
光ゼロ、温度最高の　ハ　が解
問4.　

光を強くすると、上図の（３）の列の影響が大きく、必ず酸素と二酸化炭素のバランスは必ず崩れる（酸素が多くなる）
光をゼロにすると、上図の(2)の列の反応しか起こらず、バランスは必ず崩れる（二酸化炭素が多くなる）
光を弱い光Bにすることで、（1）（2）（3）の列の反応がバランスをとって相殺することがありえる。

問題文の「また、これまでに述べた条件だけからでは1つにしぼれない場合は、その可能性があるものすべてを選びなさい。」に注意してください。実際、ロとホが同時に「実験開始前後の酸素、 二酸化炭素量が同じ」であることはありえません。

～今回の問題から導かれる出題校からのメッセージ～
「ドライバー」をさぐる意識

ロジム今週の1問ですっかりおなじみとなった常套句「構成要素」に分解する

理科・算数だけでなく、国語や社会、はたまた身の回りの困難を
処理するときにとても効果的な方法論です。

全体を動かす部分要素をドライバーといいます。
（変数≒パラメータ　と近い意味です）

全体の結果を生む構成要素は何か。

導かなくてはいけない解までの距離が遠ければ遠いほど、この「ドライバーをおさえる」
という考え方は効果的です。

本問では、全体として「酸素が増える」という結果を引き起こしているドライバーが
いったい何かを正確に樹形図としてとらえる必要があります。

全体を把握するために、構成要素の複雑な関係を把握する。
構成要素を把握するために、正確に場合分けをする。

本問は、これから各界の未来のリーダーとして、多くの複雑な問題を解決することを期待されている
皆さんにおくる、開成中学からの挑戦状であり、贈り物です。

女子学院中算数入試より。「複雑で身近なものに算数を使うための基本姿勢とは？」

1図のような、直方体と三角柱をつなげた形の五角柱の密閉された容器があり、下から15cmの 高さまで水が入っている。これをさかさまにして、水面と上の面が平行になるようにすると2図のようになる。

五角形ABCDの 面積を求めなさい。
(女子学院中）　　　

さぼらず、求めたい部分の図 形を書き出して見ましょう。

面 ABCDEを底面として考えると、
水の容積は、1図において底面はCDFG、高さは7cmとして考える
ことができ、2図においては底面ABHIE、高さは7cmとできる。

1図と2図で水の容積は同じ、高さはともに7cmであるから、
1図の底面である四角形CDFG（3図）と
2図の底面である五角形ABHIE（4図）
の面積は同じだということになる。

それゆえ、3図、4図の水と触れていない部分である
五角形ABGFEと
四角形HCDI
の面積も同じとなる。

よって求めるべき五角形ABCDEの面積は3図で考えると
五角形ABGFE＋四角形GCDF　となる。

五角形ABGFEの面積＝四角形HCDI＝7×8＝56　平方cm
四角形GCDF＝15×7＝105　平方cm
よって
五角形ABCDE＝56＋105＝161　平方cm
答え：161　平方cm

問題の図は、状況をすべて説明してくれる角度で描かれていますが、
これが問題の単純化を妨げています。

解答のような形で、求める平面図形をしっかりと把握することがもっとも大切です。

この視点で考えると、
五角形ABGFEの面積が超えなくてはいけないハードルであることが明らかになり、
方針が定まります。

今週の一問でも何度か取り上げていますが、
立体図形の単純化（＝平面化）
はとても大切な技術です。

立体図形の中の面についてとりあげる問題は、
平面図形として考えればかなりやさしい問題でも、
立体の中に描かれたままでは、辺や角の関係を正確にイメージすることはとても難しくなります。
面倒でも書き出してみる几帳面さが求められます。

～今回の問題から導かれる出題校からのメッセージ～
基本的なモデルを考える視点が大切

女子学院中の算数は、
「基本的な問題をすばやく処理する能力が問われる」
と言われますが、いざ過去問を見てみると、
教科書や基本問題集では見たことのないような図形、設定がほとんどです。

本校の問題の特徴は、
「超基本的な算数技術を、身近な題材に対して適用させる。」
ことです。

身近な題材とは、
「具体的な容器に入った水」「点ではなく人や乗り物の移動」「数の計算ではなく値段の計算」
など生活に密着してはいますが、算数の題材としては極めて数値化しにくいものです。

このようなタイプの問題に取り組むなかで、普段から
「これはそもそもどの算数の技術が問われているの か」
について検討する習慣をつけておくことが大切です。

さもなければ問題の本質とは関係のない設定に振り回されて終わってしまいます。

ほとんどの生徒にとって、算数・数学はそのもののために勉強するのではなく、
実生活で出会うものを計算、測量するためのものです。

複雑な対象を、計算可能な形に落とし込む工夫を求める本問は、
高い学識を活かし実社会で活躍する人材を輩出する本校の指導方針を反映した良問です。

学習院女子中より。「ものを考える」とはどういうことかを教えてくれる良問です。

シドニーオリンピックの聖火リレーでは、特別に開発された水中 用トーチ（たいまつ）が使われました。これは水中でも陸上と同じように、聖火が光をだして燃え続けることができる装置です。どのようなしくみにすれば、水中で聖火を燃やしつづけることができるのでしょうか。あなたの考えを書きなさい。図を用いてもかまいません。
(学習院女子中）　 　　　　　　　　

闇雲にアイデアを考えてはいけません。「発火 するとは」ということにまず落とし込みます。「要件を満たすようにうする」という言葉/考え方が最大のヒントになります。

（例 1）燃料の出口を発火点とし、火元に酸素をおくりこむ酸素ボンベをとりつける。また、この酸素によって水をたえず押し出し、発火点に水が入り込まないよう にする。また、最初に点火をしてから水中に入れる。

（例2）熱を加えると酸素を発生する物質と火薬をまぜたものを棒状にする。燃えた分だけ、棒状の装置から火薬と酸素発生物質の混合物がせり出してくるよう にする。点火後に水中にいれる。

も のが燃えるためには、
1）　酸素がある　
2）　発火点以上の温度である
3）　燃えるものがある
という条件が必要です。

本問は、この三点を満たす装置を考えることで解答の作成が可能です。

「水中トーチってどうやってつくる？」と闇雲に考えるよりも、


「酸素を十分に供給するには？」
「燃えるもの自体を供給するには？」
「火元の温度を下げないようにするためには？」
と、構成要素ごとに細分化して考えるほうが格段に思考は先に進みます。

つまり、この問題を言い換えると、
「燃焼条件を整理し、その条件ごとに対策を考えなさい」という問題になります。

実用できる完璧な装置を考えるのではなく、
「必要要素」に物事を分解するスキルを問われているのです。

～今回の問題から導かれる出題校からのメッセージ～
物事の「構成要素」に着目、そして整理する能力を身につける

物事を考えるときに、とくに、アイデアがまったくうかばないときにどうすればいいか。

受験生に限らず多くの人々が抱える悩みではないでしょうか。
そして、多くの人が抱える悩みであるのに、
それが教育という現場できちんと教えられているかというとはなはだ疑問です。
（欧米にくらべ、日本では小学生が「物事を考える方法」を教わる機会が余りにすくない！と痛感し、
そういった場の提供をするというのがロジムのそもそもの設立目的です。）

今回の問題では、
「物事を構成要素に分解することで、具体的にアイデアをすすめる」というスキルを紹介しています。

「お金もちになる方法は？」という課題に際し、思いつくままにアイデアを列挙するよりも、
お金持ちになる方法を、　１）　収入を増やす　２）出費をへらす　に分解して、それぞれの場合でさらに分解してアイデアを考えるほうが、思考は進むし、ア イデアに網羅性が生まれます。

ほかにも「ダイエットする方法は？」を「入ってくるエネルギーをへらす」「消費するエネルギーを増やす」「脂肪を除去する」というように分解して、それぞ れ考えるなどは、ロジムの授業だけでなく、「ロジカルシンキング」という分野ではおなじみの題材です。

「考える」というありふれた行為ではありますが、そこにはスキルがあるのです。

本問は、そんなスキルの一つ、「構成要素に分解する」という最も重要な思考スキルの一つを
チェックする代表的な問題です。

女子学院中算数入試より。「数えるものが見えていますか」計算力の前提となる、計算技術への理解を問う問題です。

1から120までの数字が1つずつ書いてある紙があります。
この紙に書かれている「２」「１」「０」それぞれの数字の個数を求めなさい。

(女子学院中）　 　　

教科書10ペー ジから20ページまでの宿題は、全部で11ページですよ。

・ 「２」について
一の位にあらわれる「２」は
２、１２、２２、３２、・・・・・１１２の12個
十の位にあらわれる「２」は
２０～２９、１２０の11個
百の位にあらわれる「２」はない
よって合計23個

・「１」について
一の位にあらわれる「１」は
１、１１、２１、３１、・・・・１１１の12個
十の位にあらわれる「１」は
１０～１９、１１０～１１９の２０個
百の位にあらわれる「１」は
１００～１２０の２１個
よって合計53個

・「０」について
一の位にあらわれる「０」は
１０、２０、３０、４０、・・・・・１２０の1２個
十の位にあらわれる「０」は
１００～１０９の10個
百の位にあらわれる「０」はない
よって合計２２個

答え： 「２」23個、「１」５３個、「０」２２個

単 純な「数える」問題です。
２、１２、２２、３２、・・・、１１２
が瞬時に「１２個」だと判断できるでしょうか。
２、１２、２２、３２、・・・、１１２
下線部に気をとられて11個と数えてしまう生徒（大人も）多いのではないでしょうか。
日付、ページ数など「○～△まで」を正確に数える技術と確認の癖をつけておきたいものです。

また、「位ごとに数える」という視点も大切です。
上位校で近年頻出の考え方ですので、数の並び方の確認も兼ね、
ぜひ取り組んでおきたい問題です。

～今回の問題から導かれる出題校からのメッセージ～
無意識に使っている技術の深い理解が大切

低学年で学ぶ「大きな数」や、四則演算の筆算などの単元で丁寧に取り扱われる「位」の考え方は、
10進法の仕組みを考える良い機会です。

高学年で学ぶ計算を簡単にするテクニックは、
これらの仕組みに依存しているにも関わらず
しだいに表面的なテクニックのみが頭の中に残ってしまうことになりがちです。

「位ごとに数える」などという単元はありません。しかし、
計算と数えることは似 て非なるものです。

「何を数えるのか」が正確にわかって初めて役に立つのが計算です。
自分の使っている計算技術の仕組みや、
そもそも何を数えているのかについて再度確認しておきたいものです。

たとえば場合の数の「６C２」＝６×５÷（２×１）についてきちんと説明が出来るかどうかなど
はいわゆる「応用力」の差となってあらわれてきます。
誰でも知っている（と思いがちな）題材で、仕組みの深い理解を問う良問です。

東大寺学園中より1問です。

4個の円（ア）、（イ）、（ウ）、（エ）が図１のように交わ り、10個の部分に分かれています。
　この10個の部分に0、1、2、3、4、5、6、7、8、9の数字を、同じものを2度使わないように、しかもそれぞれの円の中の数字の和が同じ値（Aと する）になるようにわりあてます。例えば、図1のようにわりあてると、
　円（ア）の和は9＋0＋3＋4＋7＝23
　円（イ）の和は0＋3＋2＋6＋7＋1＋4＝23
　円（ウ）の和は3＋4＋8＋2＋6＝23
　円（エ）の和は4＋7＋6＋1＋5＝23
となり、A＝23です。


（問）　図2の□の中にそれぞれ数字を当ては めなさい。

　　　　　　　　（東大寺学園中）

ノーヒントです。

図 ３のように、分かれている10個の部分にB ～Kの記号をつける。
円（ア）の中の数字の和は、B＋C＋D ＋E ＋F
円（イ）の中の数字の和は、C＋D＋E＋F＋H＋G＋K
円（ウ）の中の数字の和は、D＋E＋G＋H＋I
円（エ）の中の数字の和は、E＋F＋G＋K＋J

それぞれの円の数字の和の合計は等しいことに着目すると
円（ア）の合計＝円（イ）の合計より
共通部分のC、D、E,Fを除いた、B＝H＋G＋Kである。

ゆえに求めるべき数字の一つ（上の□）B＝2＋7＋0＝9
円（イ）の合計＝円（ウ）の合計より、
共通部分のD、E、G、Hを除いた　C＋F＋K＝I

ゆえに求めるべき数字の一つ（左下の□）I＝3＋5＋0＝8
円（イ）と円（エ）も同様に考えると
共通部分のE、F、G、Kを除いたC＋D＋H＝J

ゆえに求めるべき数字の一つ（右下の□）J＝3＋1＋2＝6
となる。

複 数の要素から成立しているものどうしを比較する問題です。

低学年のときに、天秤で勉強した内容の発展形です。
複数の要素から成立しているものの比較のポイントは、

「差に関係している要素はどれか」

について、正確に把握することです。

それ以外のものは視界から外す、つまり引いてしまっても問題ありません。
また、正確に把握できていれば、双方に同値のものを加えて変形させて考えることもできます。

今回は、それぞれの円の値となっている要素をきちんと列挙して、検討することが
突破口になります。低学年の教室でも正答率は高くなりました。

～今 回の問題から導かれる出題校からのメッセージ～
隠れた制限に対する探究心が 大切

魔 方陣など、一見当てはめで解けそうな問題にも、
論理的な突破口を検討する姿勢は入学後の勉強の姿勢として
強く求められるものです。

「答えを狭める要素は何かないのだろうか。」

無限に広がって見える選択肢を前にして
立ち止まりとことん考え抜く姿勢を持ったものだけが、
正答にすばやくたどり着くことができます。

答えを得ることだけが本番では大切です。
しかし、本問は、

普段の勉強の中でプロセスを大切にしてきた生徒と
そうでない生徒との間に明確な差

が生まれるようなボリュームで設計されている良問だといえます。

大阪星光学院中より1問です。普段の問題演習に対する姿勢が問われます。

下の図のような、ＡからＧまでの道があり、その距離は３０km です。道ＡＢとＦＧは平地で、他は坂道です。平地を時速４km、坂道は、上りを時速２km、下りを時速６kmで歩くと、ＡからＧへ行くのに７時間３０分か かり、逆にＧからＡへ行くのに１１時間３０分かかります。
ＡからＧへ行くとき、すべての下りの距離の和は上りの距離の和より何km長いですか。

（大阪星光中）

ノーヒントです。

問題で与えられた図は、下のように上りと下りをそれぞれ1つにまとめて考えることができます。
AからGへ行くのに7時間30分、GからAへ行くのに11時間30分かかったということは、
つまりAからGへ進むときのほうが、GからAへ進むときよりも合計の距離は同じでも、
下りの部分が多いということです。それは、下の図の丸で囲まれた部分のことです。

つまり、この部分の長さを求めればよい。
問題は、時速6キロで歩く時と、時速２キロで歩くときに
11時間30分－7時間30分＝4時間
の差がつく距離を求めるということになる。

時速6キロと時速２キロは、速度の比は3：1。
つまり同じ距離を進むのにかかる時間の比は１：３となる。
この比の差の２が4時間なので、比の１つ分は2時間となる。
時速6キロでかかる時間は２×１＝２時間、時速２キロでかかる時間は２×３＝６時間である。
よって、求める距離は
時速６キロ×２時間＝１２キロ（時速2キロで考えても時速2キロ×６＝１２キロ）
答え：１２ キロ

ポ イントは、そもそも問題において「上りと下りの合計」が問われているということ。
また与えられた時間が、AからGとGからAという単位で考えられていることです。

この状況を鑑みて、単純化つまり
「問われている数値を求めるために必要十分な形に変形」することが突破口になります。

そもそもこの単純化（モデル化）によってよけいな情報をそぎ落とす技術は、
限られた知識しか持っていけない試験会場において初見の問題を解く上でもっとも重要なものです。

本問のようにそもそもの情景自体を変形させるのは、なかなかレベルの高いものですが、
普段の問題演習のなかで、「取り組んだ問題は単純化すると、どの基本問題に行き着くのか」
について考えることは単純化（モデル化）の技術力を高めます。
本文では、有名な「峠を含んだ速さと比」の基本問題に行き着くのです。

～今回の問題から導かれる出題校からのメッセージ～
実験、体験から学ぶ基本姿勢が大切

単純化、モデル化に完全な正解はありません。
自分が同じだと思った類題が本質的には違っていたり、
違うと思っていたものが本質的には同じだったりすることが多々あります。

大切なことは、次に出会った問題、事象に自分で考えたモデルを当てはめ、修正していく仮説 検証能力です。

この能力を身につけるための大前提は、
手探りの中で仮説を立ててみるという姿勢です。
教科書の目次に並ぶタイトルが、最適な整理基準とは限りません。
（むしろ近年ではこれらのタイトルを横断した出題が意識的に増やされているとさえ言えます。）

正解のない中で、自ら試行錯誤の中で体系化を試みる姿勢は、同校の求める人物像です。
そして本問は、その姿勢を数年間の受験勉強の中で身につけてきたかを問う良問となっています。

今週 は桜蔭中より1問です。

『カエルが、からだのどこを使って産卵池の位置を知るのか』を 調べるために以下の実験を行いました。

【実験】池に向かうカエルを池から50～200ｍ離れたところでつかまえて，3つのグループ（う）、（え）、（お）に分け、以下のようにしました。

グループ（う）：目が見えないようにした後、（う）の目印をつける
グループ（え)：鼻でにおいがかげないようにした後、（え）の目印をつける
グループ（お)：目や鼻には何もせず、（お）の目印をつける
　
　グループ（う）、（え）、（お）のカエルをつかまえた場所で放し、1週間で、どれくらい池にたどり着いたかを調べた結果が図3です。

問4　【実験】の結果について、つぎの問い（1）～(4)に答えなさい。

（1） 池の位置を知るのに、カエルが主に目を使って いるといえる場合は○、いえない場合は×を書きなさい。
（2） （1）はグループ（う）～（お）のどれとどれ の結果を比べるとわかりますか。
（3） 池の位置を知るのに，カエルが主に鼻を使って いるといえる場合は○、いえない場合は×を書きなさい。
（4） （3）はグループ（う）～（お）のどれとどれ の結果を比べるとわかりますか。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（桜蔭中）

上記、（１)から(4)を解くにはヒントはい らないと思います。この問題は、解答の先にとても大事な考え方を知るチャンスがあります。必ず解説にも目を通してください。

(1) ×　
(2)　（う）と（お）
(3)○
(4）　（え）と（お）

こ の問題の隠れたポイントは、
（2）で、なぜ、（う）と（え）をくらべてはいけないか
（3）で、なぜ、（う）と（え）をくらべてはいけないか
が説明できるかどうかです。

（上記が説明できなくても試験では解答できてしまうのが残念なところです）

グループ（う）　→　目隠し
グループ（え)　→　鼻せん
グループ（お)　→　なにもしない

ソラマメの発芽実験問題が有名ですが、この問題も対照実験について扱った問題です。
「対照実験とは」　→　「比べることにより結果の理由を特定する実験」
→　「２者の異なる点が1つだけならば、生じた結果の原因は、その異なる点だと結論ずける方法論」

グループ（う）とグループ（お）　
・・・・　異なる点は、「目隠しをしているかどうか」　の1点

グループ（う）とグループ（え）
・・・・　異なる点は、「目隠しをしているかどうか」と、「鼻せんをしているかどうか」の２点

となります。グループ（う）とグループ（え）を比べても、池に帰ってくるカエルの割合が違う原因が、特定できないのです。異なる点が２つあるからです。ど ちらが理由なのか特定できません。

この問題は、本来、
「カエルが目をあまり使っていない」ことを言うために、（う）と（え）をくらべてはいけない理由を説明しなさい。
とするべきだったのではないでしょうか。　　（答えは、「（う）と（え）は異なる点が２つあるから」）

「一つの結論に対して、一つだけの相違点をみつける」
対照実験の根本を理解しているかを確認してください。

～今回の問題から導かれる出題校からのメッセージ～
「対照実験」のような基本的方法論の徹底理解をすること

以前にも同様のメッセージを読み解きました。とかく頻出の対照実験問題ですが、
上位校ほどその根本的意味の理解を確認してきます。

さて、教室で本問を扱いました。学年問わず８割の生徒は正解できましたが、こと、

（2）で、なぜ、（う）と（え）をくらべてはいけないか
（3）で、なぜ、（う）と（え）をくらべてはいけないか

という問いを追加すると、白紙になってしまう生徒がほとんどでした。
（対照実験の意味が理解できていない証拠です。）

「目隠ししても、多くのカエルが帰ってくるけど、
鼻せんをすると、ほとんどのカエルがかえってこられない。」

日常の感覚だと、上のセンテンスからでも、「カエルにとって目は大事ではない」と
結論づけることもできそうです。
しかし、この日常の感覚を疑い、科学的な方法論で物事を判断するスキルを
桜蔭中は求めているのです。

「感覚を疑え！」などと格好良く言い放つことは簡単ですが、「疑い方」が伝えられていないのが
現在の理科教育の現状ではないでしょうか。
「感覚を疑う」ことは、闇雲に疑心暗鬼になることではありません。
また、「感覚」は否定すべきものではありません。

自分の直感・常識・感覚を補強し、視点を増やすために、対照実験のような基本的な方法論を
徹底的に理解する必要があるのです。