学習塾ロジム　今週の1問by 学習塾ロジム

今週はフェリス女学院中より1問です。

大 と小のサイコロが合わせて１８個あります。この１８個のサイコロを同時にふったら、出た目の平均は４でした。大のサイコロだけの出た目の平均は3.4でし た。小のサイコロだけの出た目の平均は、どのような場合がありますか。すべての場合を求めなさい。割り切れないときは小数第２位を四捨五入して小数第１位 までの数で答えなさい。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（フェリス女学院中）

「サイコロの目」というだけで、大きな制限が ついてきます。

サイコロの目は整数1～6によって構成されています。

つまり、複数のサイコロをふったときに出た目の和は、
1～6の組み合わせである「整数」であるということが前提となります。

また、問題文の条件に大のサイコロの出た目の平均が　3.4　
つまり17／5であることが与えられています。

ここから、大のサイコロの個数は、5の倍数であることがわかります。
つまり、大のサイコロの個数は、5個、10個、15個のいずれかになります。

・大が5個の場合の小のサイコロの平均
　（4×18－3.4×5）÷（18－5）＝4.23・・・＝4.2 （割り切れないので四捨五入）

・大が10個の場合の小のサイコロの平均
　（4×18ー3.4×10)÷（18－10）＝4.25（割り 切れるので四捨五入はなし）

・大が15個の場合の小のサイコロの平均
　（4×18－3.4×15）÷（18－15）＝7・・・サイコロの目は6までしかないので不適格
　
以上より

答え　 4.2　　・　　4.75

「隠れた制限」つまり、問題文にはいちいち明記されないが、
当然の前提として答えに制限を加えるものです。

本問では、平均＝3.4から　5の倍数である　という制限を導き出すことと、
最後に「平均7」は、1～6で構成されるサイコロにおいてはあり得ない

という2つが隠れた制限になります。
このような倍数制限など、気付けば検討範囲が数通りにまで狭め ることができる典型例は、

十分に頭に入れておける数しか存在しません（例えば日付や個数 など）。
この分野のみをしっかりとピックアップした参考書はほとんど存在しません。
そして、解説のなかでは「そういえばそうだった。うっかりしてた。」といった形で受け流してしまいがちです。
一度、このような隠れた制限にどういうものがあるのかまとめておくことが必要です。

～今 回の問題から導かれる出題校からのメッセージ～
・問題文に出てくる物語を具体的にイメージす ることが大切
本問は、「サイコロ」や「平均の計算の手順」についてのイ メージを失い、
数式のみを元にして試行錯誤をしたとたんに、落とし穴にはまります。

本問に限らず、すでに長い歴史のある中学入試、
とくに上位校では単純な先取り学習で身につけた数式処理で解くことができるような問題は
ほとんど出題されません。

算数には、数学の土台としてだけでなく、

「日本語を論理的にしっかりと読む力」

「身の回りのものを工夫して測量する力」などといった力を養成 する目的もあります。



ポイントは、問題文を読みながら具体的なものをイメージすること。

問題文を一度よんで、しっかりと図解できる生徒は、イメージしながら読めている証拠です。

この作業を、面倒くさがらずに取り入れてみることで

速さ、平均など抽象的なものを数値化している世界が一気に具体的なものとして身につきます。



そうするだけで、

「直感としてあり得ない数値」をはじくことができるようになるのです。

今週は浦和明の星女子中より1問です。

明子さんとお父さんは、それぞれA地点を出発して、8km離れたB地点まで行き、すぐに折り返してA地点まで戻ってくることにしました。お父さんは、明子 さんが出発してから何分か遅れて出発し、B地点の手前3kmの地点で明子さんを追い越しました。そして、B地点を折り返した後、B地点から1kmの地点で 明子さんとすれ違いました。明子さんは、お父さんがA地点に戻ってきてから110分後に、A地点に戻ってきました。ただし、明子さんとお父さんは、それぞ れ一定の速さで歩いたものとします。

（1）明子さんとお父さんの速さの比を、最も簡単な整数の比で表しなさい。
（2）明子さんの速さは分速何mですか。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（浦和明の星女子）

速さを求めるために必要な要素は決まっていま す。

（１）上の図のC地点で、父が明子さんを追い越す。
ここを起点とすると、Dで二人が再会するまでに、
同じ時間で父は〔C～B〕＋〔B～D〕＝4km歩き、
明子さんは〔C～D〕＝2km歩いたことになる。

よって、速さの比「明子さん：父」＝2：4＝1：2　答え　1：2　　

（２）（１）と同様に、C地点を起点に考えると、C地点を同時に出発したあと、
Bを折り返し地点としてAまでの11kmで110分の差がついたことになる。
二人の速さの比は、1：2なので、同じ距離を歩くのにかかる時間の比は2：1である。

この比の差である1が110分であったのだから、
明子さんがCからBを経由してAまでの11kmを歩くのにかかった時間は、110×2＝220分である。
よって、明子さんの分速は　11000（m）÷220（分）＝50m/分
答え　 50m/分

速 さ＝距離÷時間
速さの比は、「同じ距離」を移動するのにかかった時間の比
といった、当然の定義を見失わないことが大切です。

速さと比の問題は、様々な場所や、
出来事（折り返し、忘れ物による引き返し、途中で速度が変わるなど）によって、
問題文が長く、見た目が仰々しいものが多くなっています。

しかし、突破口は1つです。
速さ、距離、時間のうち、2つが揃う場面を探し出すことです。

本問でもC地点で父が明子さんに追いついてはじめて、
「2人が同時にスタートした」という条件がそろいます。
「どこから解いたらよいのか分からない」は、
「なにがわかれば答えがでるのか」という意識の欠如が大きな原因です。
速さの場合は基本は3つの要素です。
「必要な要素を洗い出して確認する」ことが基本です。

～今回の問題から導かれる出題校からのメッセージ～
・定義の深い理解が大切
速さを求めるのに一体何が必要なのか。
これは、難しいことではありません。

ただし、表面的な複雑さに目を奪われ、自分が今何を求めなくてはいけないのか、
についてしっかりとした方針が立てられないと、求値のための作業に集中できなくなります。

このレベルの問題は、「何を求めるのか」が決まったあとの計算も複雑なものになりがちです。
この複雑さによって、一行問題にかわり計算力を試しているともいえます。

つまり、正確に「これを求めれば答えにたどりつく」という方針をたてていないと、
長く複雑な計算の末に無意味な数値にたどり着いてしまうのです。

「何を求めるのか」は、数少ない選択肢を正確に確認しさえすれば
明らかになることが多いものです。

絶対に必要な要素の有無の確認は、定義についてしっかりと理解していることを
必要とするまさに質の高い基本問題といえる良問です。

今週は岡山・金光学園中より1問です。

図1は、地球儀を電燈で照らしているところを示しています。図 2は、図1を真上から見た図です。また、A～Hの地点には、マッチ棒を垂直に（地球の中心に向けて）立てています。電橙を太陽と考えて、次の問いに答えなさい。

（l）図のように光を当てているときA、B、Hの地点のマッチ棒のかけはどのようにできますか。下の（ア）～（ク）から選びなさい。

（2）地球の自転の方向は、図2のア、イのどちらですか。
（3）地球儀を回転させて、真北にできるマッチ棒のかけの長さを見るとき、D地点のときにできるかげの長さと等しいかけができる地点はどこですか。
（4）A地点は、ちょうど太陽が南中しているときにあたります。G地点の時刻は何時ですか（午前・午後を使って答えなさい）。　　　　（金光学園）　　　 　　

図 1や図2をにらめっこしていると余計に混乱します。そもそも影の長さと向きは、差し込む太陽の方向と高度が決めるということに立ち返ってみてください。

（1）　A・・・ア　　B・・・ク　　C・・・ウ
（2）　イ
（3）　F
（4）　午後6時

（1） まず、A、D、H　の位置での観測時、太陽が南中しているから、影は真南・真北にのびる。
　　（↑　上記解説の意味が分からない人は、もう少し学習がすすんでからこの問題を考えること）

上図のように、A・Hそれぞれの位置の地平線がどうなっているのかを考える。
A　は南側から太陽の光が当たる　→　影は北にできる　→　（ア）か（イ）
H　は北側から太陽の光が当たる（30-23.4＝6.6度分だけ）　→　影は南にできる　→　（ウ）か（エ）

Aの影が（イ）だとすると、それより影が明らかに長くなるHでの影を（ウ）か（エ）から選べない。
よって、Aの影は　（ア）であり、Hの影はそれより明らかに短い（ウ）　となる。

Bに関しては、Aと同じ緯度であるため、Aと同じ角度で、南側から太陽がさしこむ。
また、自転の方向を考えると太陽は西側から差し込む。　
つまり　南西から太陽の光が差し込む　→　影は北東方向にのびる　
したがって解答を得る。

（3）　マッチ棒の長さが共通ですから、影の長さはそれぞれの位置の地平線に対する、
　　　太陽の差し込む角度によります。　
　　　太陽の差し込む角度は、緯度が同じならば同じです。よって、Dと緯度が同じFが解答。

（4）　時差をきめるのは経度です。
（同一経度上の時刻は等しいということの詳細解説は割愛します。
この図で言えば、例えばC-F-G　は同じタイミングで南中を迎えます。）

したがって、Gの南中時刻とCの南中時刻は等しい。
CはAにくらべ、90度東側に存在する。つまり　90度分、例えば、先に南中を迎えたり、朝日を迎える。
360度回転するのに24時間かかるので、90度分だと、6時間分　（360度：24時間＝90度：時間）
先に南中を迎える。

～今回の問題から導かれる出題校からのメッセージ～
・ 仕組みを理解して初めて暗記を行うこと
　　→　暗記はしようとしてするのではなく、完全な理解と同時に自然としてしまうもの
理科天体分野ほど、教科書知識の丸暗記により点数を落とすことにつながる
分野はないでしょう。

頭の中で物事をグルングルン動かさなくてはいけないという性質上、この分野を苦手とする生徒は
大変多いのが実情です。

「上弦の月の一週間後は満月だ」　
「北極星の周りを星は反時計回りに回る」
「夏のほうが日が長い」
「月の公転周期と、満月から満月になるまでの期間は2.2日ずれる」
「冬至の日の南中高度は90度－緯度－23.4度だ」

などということを、他者に説明できない状態で暗記していると、

「あれ、上弦だっけ、下弦だっけ？」
「あれ、南の空では反時計？時計回り？」
「南半球ではどうなるの？単純に反対？」
「冬至の南中高度の式中の記号はプラスだっけマイナスだっけ？」

などと、すぐに受験生の暗記主義を打ち崩すべく用意された問題に混乱することとなります。
たとえば、本問（１）でも

「冬の季節に北半球では太陽は南側を通って東から西へ進む」という知識からでもA＝ア　は解答可能です。ですが、上記カッコの丸暗記で済ませている場合、 Hを考える際に「あれ、南半球の時はどうなるんだっけ」と戸惑うことは必至でしょう。丸暗記で足元をすくわれることの多い事の例です。

前回の今週の1問でも書きましたが、
「とりあえず覚えてしまえ」という勉強法および指導法は、
長く将来にわたって活きる能力をつけるという目的に対しては悪です。

自分が原則を理解したうえで学習を進めているのか、
（上に紹介した天体分野の約束事を他者に説明できますか？？）
自分の教師は将来にわたり役立つ学習指導をしているのか
（あなたの指導者は「とりあえず覚えちゃって」などと言っていませんか？？）
を計るのに良い機会を提供してくれる１問です。

今週 は筑波大付属中より1問です。

7／2　ｍのひもを切って、1／3ｍのひもをつくります。ひも は何本つくれますか。また、何ｍ余りますか。　　　 　　

商とあまりの単位。そして、割り算の意味をきちんと確認しましょう。

7／2 ÷1／3　　＝　21／2　　　　　　となる。
この割り算の商である　21／2　は、
7／2　の中に、1／3　が　21／2　本とれるという意味である。

つまり、きちんと　1／3　ｍとれたひもは10本であり、
それに　1／2　　本という足りないものがあまるということ。

1／2　　本＝　1／3　×　1／2　＝　1／6　ｍ

つまり、あまりは、　1／6　　　ｍとなる。

答え 10本とれて　1／6　　ｍ余る

ま さか、こんな簡単な問題に、、。と、
当時の優秀な受験生たちが何人も引っかかった問題です。
誤りはすべて、あまりを1/2としたものです。

割り算の意味「相当の計算」「分配の計算」をしっかりと理解し、
商、あまりの意味（＝単位）をきちんと意識できるのかどうかが試されました。

四則演算の意味を正しく理解していなければ、
中学以降の文字を使った数式中心の世界を渡っていけません。
特に難しく、奥の深い「余り」を中心にしっかりと意味を考える時間をとっておきたいものです。

～今回の問題から導かれる出題校からのメッセージ～
・ 「計算方法を知っている」ことと、
「計算の意味を理解している」ことは違う
・「筑波大附属は、基本問題中心だから、基本問題集を何度もくり返すべき」

本校に限らず、よく聞かれる浅はかな過去問分析です。
特にハイレベル校において、
「基本問題中心」とは、「計算問題や教科書的典型問題をスピーディーかつ正確に解かせる問題構成」という意味ではありません。

四則演算や図形の成り立ちなど、基本原理を活用して、複雑な問題を美し く解く。
と定義したほうが近いでしょう。

基本原理は、必ず（とくに小学校の教科書や塾の導入章において）説明されています。
その部分を飛ばして、表面的な演習（つまりとりあえず慣れろという方法論）に走る子どもたち（むしろ指導者たち？）に強く警鐘を鳴らす問題です。

例えば、ガウスの等差数列の和の公式と台形の面積の求め方の基本原理は同じです。
どちらも必ず習う公式ですが、基本原理の類似性をしっかりと理解していると、
この2分野以外でも応用のきく考え方になります。

折角たくさんの問題に取組むのです。帰納的に収斂させ、検証するという作業を加えることで、
高い仮説検証能力を身につけることに繋がります。
「基本事項からの出題」という縛りの中で、ハイレベルの受験生に対応してきた本校の問題は、
「基本」の大切さをきちんと理解できる生徒を選りすぐるのに適した良問となっています。

市川中より1問です。

下の図のようなおうぎ形OABがあります。このとき，次の問い に答えなさい。
（1）円周率は3.14とし、おうぎ形OABのまわりの長さを、四捨五入して上から3けたのがい数で求めなさい。
（2）円周率を3として計算すると，おうぎ形OABについて，いくつかの問題が起きます。この間題の1つを13字以上52字以内で説明しなさい。(市川中）

（２） は（１）を導入として使ってみましょう。

（１）弧AB＝2×3.14×1/6＝1.046・・・
よって半径2つ分を加えると
1＋1＋1.046・・・＝3.046・・・
うえから3けたのがい数に 直すと
3.05
よって
答え　 3.05平 方センチメートル

（２）
（１）におい て、求めた弧ABの長さは、円周 率を3とするｔ
2×3×1/6=1
となり、半径と 同じ長さになる。
つまり、おうぎ 円ではなく、明らかに正三角形となってしまう。

（１）を導入に使うことが、唯一の突破口。
あとは、何百回としてきた円の面積、周の計算をどのように見つめてきたかが問われました。

導入授業で最初に示された後、
ほとんど触れられることのない公式や定数の意味をしっかりと捉えなおす出題は、
超上位レベルの学校で 出されても低正解率になります。

しかし、数の性質と同様、普段何気なく処理し ている手法の仕組みは、
大学入試にまで応用が利くとても重要な考え方です。
3年、4年、5年で「初めて習ったときの説明」を再度確認してください。
勉強が進んだ後でも、大きな気付きがあるはずです。

～今 回の問題から導かれる出題校からのメッセージ～
・出会った知識を掘り下げる探求心こそがすべて

円周率3騒動
（実際は、円周率を3としてすべての指導が行わるという方針だったたわけではないのですが、
大騒ぎでしたね。）の時の出題です。

当時は、東大でも似たタイプの出題がありました。

「文科省への出題による抗議」という特異な時代背景を持った出題だと捉えず、
算数の勉強姿勢を正すきっかけとしてもらいたい出題です。

そもそも、円周率とは何の「率」なのだろうか。
円の面積を求める仕組みはどのようなものか。

小学生が知識として叩き込まれるものの成り立ちには、先人たちのとても柔軟な発想が寄与しています。

「身の回りのものを測量できればよい」という立場では、
これらはブラックボックスの中に入れたままにしても全く問題はないでしょう。
それどころか、余計な体力を使わずに済みます。

しかし、皆さんが進もうとしている中学校は、
数学を含め新しい知の枠組みを作り出す人間を育てようとしている学校です。

「とりあえず入学してから。」「まずは目先の試験。」といった姿勢は、
結局は入学後も続き、大学受験の訓練場としてしか中学・高校の場を活かすことができないでしょう。

何よりも、ものの成り立ち・背景・本質にこだわる。

この姿勢を身につけることは、志望校対策の何倍もの力を身につけさせてくれることでしょう。
当時も今も、過去問分析に奔走する関係者に、学校が本当に欲しい人物像を見せ付けてくれる良問です。

～今回の問題から導かれる出題校からのメッセージ～
・ 「計算方法を知っている」ことと、
「計算の意味を理解している」ことは違う
・「筑波大附属は、基本問題中心だから、基本問題集を何度もくり返すべき」

本校に限らず、よく聞かれる浅はかな過去問分析です。
特にハイレベル校において、
「基本問題中心」とは、「計算問題や教科書的典型問題をスピーディーかつ正確に解かせる問題構成」という意味ではありません。

四則演算や図形の成り立ちなど、基本原理を活用して、複雑な問題を美し く解く。
と定義したほうが近いでしょう。

基本原理は、必ず（とくに小学校の教科書や塾の導入章において）説明されています。
その部分を飛ばして、表面的な演習（つまりとりあえず慣れろという方法論）に走る子どもたち（むしろ指導者たち？）に強く警鐘を鳴らす問題です。

例えば、ガウスの等差数列の和の公式と台形の面積の求め方の基本原理は同じです。
どちらも必ず習う公式ですが、基本原理の類似性をしっかりと理解していると、
この2分野以外でも応用のきく考え方になります。

折角たくさんの問題に取組むのです。帰納的に収斂させ、検証するという作業を加えることで、
高い仮説検証能力を身につけることに繋がります。
「基本事項からの出題」という縛りの中で、ハイレベルの受験生に対応してきた本校の問題は、
「基本」の大切さをきちんと理解できる生徒を選りすぐるのに適した良問となっています。

今週は麻布中理科より1問です。

　生き物の体は，脳もふくめてたくさんの正常なたんぱく質でつくられています。ウシの海綿状脳症（狂牛病）は，異常なたんぱく質が体の中に入り，それが病原体となって起きます。この異常なたんぱく質が脳に入ると，脳が必要としている正常なたんぱく質が足りなくなって，脳が海綿状（スポンジ状）になってしまうのです。
　ヒトでも，狂牛病の病原体と同じような異常なたんぱく質が体に入ることにより，脳がスポンジ状になる病気が知られています。その異常なたんぱく質Xはヒ トの体に入ると，正常なたんぱく質AをXに変える働きをします（図1）。XはAを変化させますが，自分自身は変化せずxのままです。また，このXがヒトの 体の中にまったく無いときAはxになりません。
>
問1　なぜ，このXが体の外から少量でも入ると，重大な病気になってしまうのですか。図1から考えて説明しなさい。

問2　もし，このXがAをXに変化させるときに，自分はYという別のたんぱく質に変化してしまうとすると，XとYの量はどうなりますか。下のア～カの中か ら，正しいもの2つを選びなさい。
ア．Xは増えていく　　イ．Xは変わらない　　ウ．Xは減っていく
エ．Yは増えていく　　オ．Yは変わらない　　カ．Yは減っていく
　　

　上のように，ヒトの体の中でつくられたたんぱく質が，それ自身をつくることに関係していることはよくあります。体に必要なたんぱく質Cはそのようなたん ぱく質で，たんぱく質Bからつくられます。そしてこのCは，BからCへの変化をおさえる働きをします（図2）。またBはいつもつくられていて，Cはゆるや かに分解されています。
>
間3　つぎの（1），(2)の場合，BからCがつくられる量はどうなりますか。図2を参考にして答えなさい。
　（1）　何らかの原因でCの量が増えたとき
　（2）　何らかの原因でCの量が減ったとき

問4　ヒトの体を健康に保つために必要なたんぱく質の多くは，図1のXをつくるような経路ではなく，図2のCをつくるような経路でつくられます。そうなっ ている利点について図1，図2を比べて説明しなさい。　

たんぱく質Aが仮に、10個だけ存在し、そこにたんぱく質Xが1個投入されると。。。。　とシミュレーションしてみてください。

問1 　
Xの作用により、AはXとなる。XはXのままであることから、時間がたつと正常なたんぱく質AはすべてXとなってしまうから。

問2
エ,　イ

問3
(1)減る　(2)増える

問4
図1の経路だと特定のたんぱく質が極端に増えたり、減ったりするが、図2の経路だと、特定のたんぱく質が増えたり減ったりしても、それを抑える方向の働き が生じ、たんぱく質の量が一定に保たれるという利点がある。

問 1　
仮に正常なたんぱく質Aが１０個あるとします。そこに、1つの異常たんぱく質Xが混じると、1個の正常たんぱく質Aが1個のXとなります。つまり、Aが9 個、Xが2個。つぎには、この2個のXの働きで、A2個がXに変化するので、Aは7個、Xは4個となります。この動作を繰り返すとAはなくなってしまいま す。

１０A　+　X　→　9A　+　2X　→　7A　+　4X　→　3A　+　8X　→　0A　+　11X

問2

・AはXになる
・もとからあったXはYになる

以上から、全体としては　AがYに変わる　変化だと考えることができる。
つまり、Xの量は不変、Yの量は増える。

問3
「Bは放っておくとCに変化し、つくられたCは今度は自分が作られるのを邪魔する」とイメージします。

Cが増えると、B→C　の変化は邪魔されます。
Cが減ると、B→Cの変化は邪魔者が少なくなり、B→Cの変化量は増えます。

問4
問3から考えます。
Cが増えると、BからCが作られる変化はおさえられ、結果、Cはそれ以上なかなかふえません。問題文にあるように、Cがゆるやかに分解されると、Cは減る ことになり、BからCが作られる変化は促進され、結果Cは増えます。そしてCが増えると・・・・

と増えては減り、減っては増えるというプロセスを延々と繰り返すことになります。
これにより存在するたんぱく質の量が一定に保たれます。

とある最適な量のたんぱく質を保つという人間のメカニズムです。

～今回の問題から導かれる出題校からのメッセージ～
・いくつかの結論を重ねて、求められる結論に到達する持久力が必要

まず気付いてほしいのが、本問は生物分野の知識は何一つ必要とされてはいない点です。
題意を噛み砕いて説明すれば、小学校低学年の生徒でも回答可能です。
純粋に、「AならばB」「Aだ。ということはBだ。」という思考を積み重ねることで回答する、
論理思考力を計る問題です。

結局この問題で必要とされる能力・技術とはなんなのでしょうか。
それは、公式やパターン学習を完全に捨てた、結論を積み上げる持久力です。
簡単に言えば、バテずに「ってことは」を積み重ねる力です。

一つの結論が出た後に、その結論をつかって新たな結論に向かう。そしてさらに、その次の結論に。
大人にとっては普段から慣れたこの能力・スキルですが、小学生にとっては我々の想像以上に
困難な作業となることがあります。特に、積み重ねるべき結論の数に比例して音を上げる生徒は
増えるのです。

論理思考力と言われるものは、往々にして脳の「結論積み上げ持久力」だと言い換え可能です。
普段から、安易に答えを確認しようとせずに、複数のヒントから答えにたどり着くという、「積み重ね」
を訓練する環境を作ることが必要です。

分からなかった問題に対して、答えや解説を提示するのではなく、
ヒントを徐々に与え答えまで導くような学習環境づくりこそ、保護者・先生のやるべきことだと思います。

今週はフェリス女学院中より1問です。

下の図のように、直角三角形ABCと半円があります。
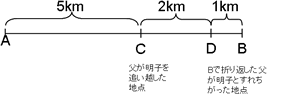
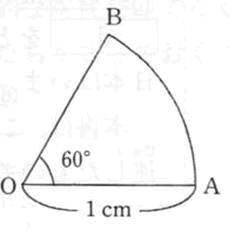
部分と部分の面積の合計は136．97cmです。
部分の面積を求めなさい。　（フェリス女学院中）

まさに分野融合問題です。

問題 の図を下のようにア～ウの3つの部分に分けて考える。

問題文の条件より、イ＋ウ＝136.97である。・・・（１）

ここで、イ、ウにそれぞれアを加えて、半円、直角三角形として考える。
ア＋イの半円の面積は13×13×3.14÷2＝265.33
ア＋ウの直角三角形の面積は15×26÷2＝195
この2つの値の差は、そのままイとウの差として考えることが出来る。

よって
イーウ＝70.33・・・（２）

（１）と（２）より
和差算によってイ、ウを算出できる。
イ＝（136.97＋70.33）÷2＝103.65

答え 103.65cm

04: 解説
前 回の灘中の問題の最後の山場を乗り越えるための練習問題です。
面積における、和差算は単純なものであっても、相当の問題文読解力が求められます。
「和」という条件から、「差を探す」という流れが身についているかどうか。
問題形式が図形であっても、割合であっても、速さであっても同様です。

～今回の問題から導かれる出題校からのメッセージ～
・所与の条件を丁寧に類型化する力が大切
前回の灘中の問題と同様、表面的な題材の形式とそこで使われる技術は、
塾の一般的なカリキュラムほど単純なものではありません。
図形の和差算、速さの消去算など、数多くの融合問題が存在します。

速さは・・・、流水算は・・・という単純なパターン解法の暗記では対応できません。
必要なのは、
問題分によって与えら れる条件が、どの方針に誘導しているのかを見抜く力です。

「分からない数と与えられた状況の数が同じならば消去算」
「和を与えられる場合は、差を見つければ和差算で答えが出る」
など、解法の本質をつかんでおくことが重要です。

途方もない作業のように思えますが、無駄な何百もの問題演習よりも時間もかからず、
頭を使って普段の勉強をまとめるクセがつきますので、是非取り入れてもらいたいものです。

フェリスをはじめとして、このレベルの勉強が要求される入試問題を出題する学校は限られています。
しかし、出題されないからといって、考えない勉強法が身についてしまうと、
想像以上に入学以降の勉強に手間取ることになるのです。

学校の指導方針と強い信念が読み取れる良問です。

今週は灘より1問です。

下の図で、ABとCDは垂直になっています。AE＝24cm、 BE＝6cm、CE＝18cm、DE＝8cmになっています。円の面積は785cm となっているとすると、斜線部分の面積の和を求めなさい。

公式で求めようのない図形の面積を測定するには、いくつかの方針しかありません。

下の 図のように、CDに平行な補助線KLとABに平行なHGを、AB、CDと対称となるように引きます。
（交点にはそれぞれ記号をふります。）
問題の円を下のようにア～ケの9の部分に分けて考える。
斜線部＝ア＋イ＋カ＋ケ
残り＝キ＋ク＋エ＋ウ＋オ
である。
斜線部と残りのそれぞれを構成する部分を比較すると
ア＝キ、イ＝ク、カ＝エ、ケ＝ウであるので、オの部分の面積がそのまま両者の差となる。
オの面積はIE×EF＝18×10＝180となるので、
和差算を使い、（785－180）÷2＝302.5cm

答え　 302.5cm

図形は単純ですが、いくつもの思考の山場がある難問です。
まず、本問のようないびつな図形の面積は、そのまま求めることはできません。

1）等積・相似の基本図形を見つける。
2）基本図形に分解する。
がオーソドックスな方針です。

2）で補助線による分解が本問の方針となります。
基本図形とは、
「正三角形や正方形、おうぎ形、等脚台形などの求積が容易なもの」、
「問題の図形と合同、相似なもの」
「対称性のある形」
の3パターンと考えてよいでしょう。

本問では、「対称性のある形」に分解してみます。
この分解という作業に短時間で論理的に
（つまり上述の基本的な選択肢の外に無駄に陥ることなく）たどり着くことが、
本問において測定されている能力といっても過言ではないでしょう。

解答のような、和差算タイプの求積問題は、一度は取組む基本問題です。
（これまで出会ったことのない人は、今回がその機会でしょう。）
そこにたどり着くまでの条件を整えさせるという難問です。

～今回の問題から導かれる出題校からのメッセージ～
・思考の類型化が大切
算数のカリキュラムは、題材によって分けられています。
例えば、速さ、面積、割合・・・・。
しかし、本問はそのような題材ごとのパターン演習のみで作り上げられた算数の力を
簡単に切り捨てる問題です。

中学受験算数の題材がどのようなものかは、
テキストの目次や過去問の分析表によって明らかになっています。
しかし、どのような頭 の使い方が要求されているのかに着目して勉強し、
内容を整理している生 徒はほとんどいません。
この問題を単なる求積問題の一つとして片付けているようでは、いくら量をこなしても、
このレベルの問題の要求に答えることはできません。
あるトップクラスの生徒は、本問について「ベン図の考え方と似ているかな？」と
ノートに書き記していました。自分の頭で、思考の類型化を試みている確かな証拠です。

「総合問題」とは、見たことのない題材に、基本的な思考方法を当てはめる問題です。
その「基本的な思考方法」をきちんと整理することを怠っていると、
教科書の範囲名の書いていないテストが始まる時期、全く手も足もでなくなります。
出来る子は、自然と頭の中でやっていて、出来ない子はやっていない。
そして普通 のカリキュラムは、これを要求する形では並んでいないのが現状なのです。

この差を地頭の差といって、諦めるのではなく、勉強の中つねに
「これはあの問題と頭の使い方が似ている。」といったフォローをしてあげることが指導者、
保護者として大切な作業です。

今週は豊島岡女子中・理科より1問です。

アサガオは，夏の早朝に花が開く植物ですが，なぜ朝に花が開く のでしょう。このような疑問を持った東京に住む豊子さんは次のような実験を行いました。その実験と結果に関する以下の問いに答えなさい。

【実験方法】いくつかの鉢を用意してアサガオの種をまき，夏休みに花が咲くように準備しました。8月の初めにつぼみをつけたアサガオの鉢植えを，次のよう な条件にして，花が開く時刻を観察しました。
　　　　　　　　　　　　　　　　　　　　　　　
粂件1 日の当たる庭 （日の出午前4時50分頃，日の入り午後6時50分頃）に置く。
粂件2 外からの光が いっさい入らない部屋の中で電灯をつけ，ずっと明るい状態にする。
粂件3 条件2と同じよ うにずっと明るい状態にし，6日目の午後4時頃から7日日の午前11時頃まで電灯を消し暗い状態にする。
粂件4 条件2と同じよ うにずっと明るい状態にし，6日目の午後7時頃から7日目の午前11時頃まで電灯を消し暗い状態にする。
粂件5 条件2と同じよ うにずっと明るい状態にし，6日目の午後11時頃から7日目の午前11時頃まで電灯を消し暗い状態にする。

【実験結果】
条件1：日の出時刻とほぼ同時刻に花が開いた。
条件2：花は開かなかった。
条件3：7日目の午前2時頃に花が開いた。
条件4：7日目の午前5時頃に花が開いた。
条件5：7日目の午前9時頃に花が開いた。

（1）アサガオと同じ時期に花を咲かせる植物を，次のア～オから一つ選び記号で答えなさい。
　　ア．アブラナ　　イ．スイセン　　ウ．イネ　　　　エ．アジサイ　　オ．ツツジ

（2）実験結果から，アサガオの花が開く理由はどのように考えられますか。次のア～ウから正しいものを一つ選び記号で答えなさい。
　　ア．アサガオは，明暗とは関係なく花を開く。
　　イ．アサガオは，明るい状態から暗くなって一定時間後に花を開く。
　　ウ．アサガオは，暗い状態から明るくなって一定時間後に花を開く。
　　　　　　　　　　　　　　　　　　　　　　　　　　　
（3）実験結果から考えて，夏のこの時期，北海道と沖縄ではアサガオの花が開く時刻はどのようになると考えられますか。それぞれについて，次のア～クから 一つずつ選び記号で答えなさい。
　ア．その地域の日の出時刻とほぼ同時刻に開く。
　イ．その地域の日の出時刻よりも早く開く。
　ウ．その地域の日の出時刻よりも遅く開く。

（4）実験結果から考えて，実験の時期を秋にずらしていくと，アサガオの花が開く時刻はどのようになると考えられますか。次のア～クから一つ選び記号で答 えなさい。
　ア．その日の日の出時刻とほぼ同時刻に開く。
　イ．その日の日の出時刻よりも早く開く。
　ウ．その日の日の出時刻よりも遅く開く。

　　　　　（豊島岡女子）　　　　　

アサガオが咲く条件を【実験方法】【実験結果】から導き出すことが第一歩です。そのために、条件を整理しましょう。

(1)ウ　(2)イ　(3)北海道…ウ　沖縄…イ　(4)イ

解説
まず、条件の整理からです。
（受験勉強に限らず、問題に当たったら手持ちの情報を視覚化整理し、
帰納法的に仮説を導くことは必要不可欠な能力です。）
下記の表のようなものを手書きでささっと書けるようにはなってほしいものです。

条件1：　18時50分（日の入り）→04時50分（日の出）（開花）　
条件2：　ずっと明るい状態
条件3：　16時（消灯）→02時（開花）→11時（点灯）
条件4：　19時（消灯）→05時（開花）→11時（点灯）
条件3：　23時（消灯）→09時（開花）→11時（点灯）

多くの受験生が問題を読む前は、
「アサガオは、日の出をサインに開花するはずだ」
ということを常識として考えています。

が、上のように条件を整理していくうちに、

「いや、ま てよ。。。　条件3,4,5　をみると、真っ暗闇の中でも咲いてるな・・・。ってことは・・・」
と考えるでしょう。

この「ってことは・・・」が大事なのです。
ここまでくればあとは多少の試行錯誤の結果、

「開花している場合、いずれも消灯から10時間で開花する！」

という仮説に行き当たるはずです。（（２）解答参照）
この時点でこの問題の勝負はありです。一山は超えました。

次に、問題(3)です。
---------------------------------------------------
まず、北海道―東京―沖縄で違うもの、ここで考えるのは
1.　経度の違い
2.　緯度の違い
です。
---------------------------------------------------

1.経度の違いを考えて、「北海道のほうが、
東京、沖縄よりも日の出が早くて、日の入りも早い」と言うことに気付くとします。
その後、先に進むとポイントは日の出日の入りの時刻ではないことに気付きます。
（結局日没→日の入りの「時間」は経度に左右されない。時刻は変わる。自分で納得するまで
地球儀を回し続けるべきです。暗記はしないで下さい。）

経度の違いは本問では意味がないのです。

２.緯度の違い
緯度が違う　→　昼の長さが違う

ここまでくればさらに一山超えました。

夜の時間：　沖縄＞東京＞北海道

東京は、日没から開花までの時間（10時間）がちょうど日没から日の出の時間でした。　

沖縄は、夜が東京のそれより長いのですから、

開花は日の出の前です。

北海道は、夜が東京のそれより短いのですから、

開花は日の出の後です。

となります。
この問題のポイントは、沖縄と北海道の開花時刻を比べてはいないことです。
開花時間に着目し、また東京の本ケースでは、日没→日の入の時間がちょうど10時間であることも、
はっきりとあまたに入れておく必要がある。

（4）ですが、
秋に近づくとは、つまり夜が長くなるのですから、開花は日の出時刻より遅くなります。

～今 回の問題から導かれる出題校からのメッセージ～
・常識を捨てて実験から仮説を導けるか

高校生になると数学の教科書に登場する「帰納法」という概念。
もともと帰納的な思考とは、
「いくつかの断片的な事象から『いえそうな事実≒仮説』を結論として導き出すこと」です。

これ自体は、もちろん小学生から日常的に行っていることです。
「黒い雲が空に広がっているときは、雨が降るだろう」
という仮説を立てたり、
「盆地がある県はくだものの生産量が多い。したがって、盆地のある福 島県では果物生産が盛んなはずだ」
と仮説を立てたり、
日常生活から入試問題 まで利用されるもっとも基本的な思考フレームです。

本来小学生のうちから思考方法として教わるべき帰納的思考。
これを我々が始めて教わるは、高校数学教科書の中で、
n　だの　n＋1　だの難しい「スウガク」として習う時なのです。これは悲劇です。

本問でも「複数の実験結果から仮説を出す」という帰納的思考がない限り、
「日の出を合図ににアサガオは咲くはずだ」という一般的な常識に縛られて解答不能となります。

ロジム授業、今週の1問でくどいように繰り返しますが、
「よく聞く常識、あたなの常識から離れて、
与えられた情報の整理から新たに仮説をつくる」という能力がここかしこで求められているのです。

・キーパラメーター（重要な変数）を絶えず念頭におけるか

また、開花に関するのが、暗くしてからの「時間」であることを意識すれば、
北海道－東京－沖縄の比較ポイントが「東西」ではなく「南北」になることがわかるはずです。

本問で経度に気をとられて拘泥した人は、
注意する変数が「時間」であって「時刻」ではないということへの意識不足でしょう。

なにも「変数」という難しい考え方をしなくても、「今どの単位に着目すればいいのか」という
意識をより強固にもってほしいものです。

今週は東邦大東邦中より1問です。

直径10ｃｍ、深さ30ｃｍの円柱の容器いっぱいに水が入って います。
この容器を下の図のようにゆっくり傾けました。
容器を45°まで傾け、もとに戻したとき、容器の中に入って いる水の深さは何ｃｍになりますか。　　　　　（東邦大東邦中一部改）

単純化できないか考えましょう。

下の 図のように真横から見て考える。
傾けたときの水面と、地面は平行になるので、三角形ＡＢＣは、直角二等辺三角形となる。
ＡＣ＝10ｃｍであるから、ＡＢも10ｃｍとなる。

ＡＢ＝10ｃｍとしたとこ ろで、こぼれた部分の体積を考える。
下の図のよう に、高さをＡＢ＝10ｃｍ、底面の直 径10ｃｍの円柱を考 えると、
こぼれたのはこの半分にあたることがわかる。

よって、こぼれ たのは、5×5×3.14×10÷2＝392.5cm
残った水の量 は、5×5×3.14×30－392.5＝1962.5cm
もとに戻したと きの高さは、1962.5÷（5×5×3.14）＝25cm
（答え）　25cm

立体の問題の中に、角度が含まれている問題で す。
空間座標を学んでいない小学生の場合、
この条件から
「平面図形に持ち込もう」

という方針をしっかりとたてられるように勉強内容を整理していることが必要です。

ここをクリアーしたあとは、「こぼれた部分が、円柱の半分である」という求積の方針ですが、
これは受験までに必ず類題に出会うものですから、問題はないでしょう。

～今回の問題から導かれる出題校からのメッセージ～
・複雑な事象の単純化・検証能力が大切である

ここまで「理系研究者に必要な能力を問お う」
という姿勢が顕著な学校もなかなかない東邦大学東邦中の出題です。

類題は、ここ何年かで筑波大附属などでも見られていますが、
解答の単純さほど簡単に解けるものではありません。

かつての中学受験生と比べ、最近の生徒に大きくかけていると感じる能力の一つが

「言い換え」「モデルの変形」

といった単純化の能力です。

単純化は、その場その場での試行錯誤と、検証能力が伴わなければ実現できませんし、
なによりもそこまでねばり強く考える時間を取れていないことが原因かもしれません。

多くの問題にあたり、高いパターン認識力を鍛えることで、
たとえ最難関校であっても合格するレベルを確保するのは難しくありません。

ただ、この試行錯誤→単純化→検証というサイクルを身につける良問に取組む
貴重な機会を見逃してしまうはあまりにももったいありません。

理系研究者だけでなく、最前線で活躍する社会人にとって必要な力を問いかける良問です。