|
市川中より。立体の問題ですが、求められるのは平面図形の高い分析能力です。

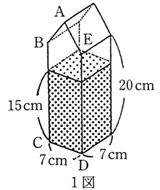
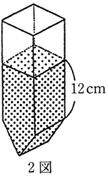
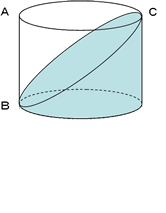
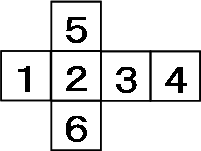
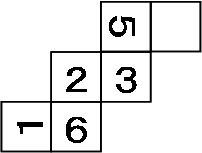
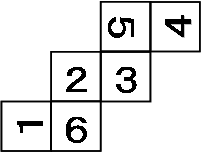
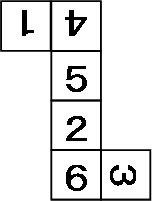
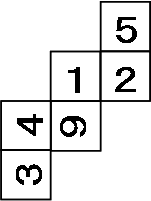
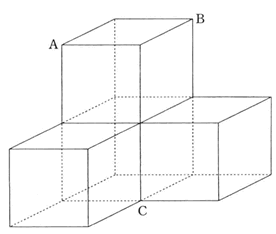
下の図は1辺4cmの立方体を点A、P、Qを通る平面と、点B、Q、Rを通る平面で切断し、2つの三角すいを切り取った立体です。この立体の表面積を求め な さい。ただし、点P、点Q、点Rはそれぞれ立方体の辺のちょうど真ん中の点です。
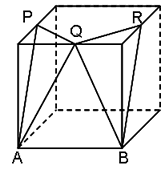
(市川中)

三角形PQAとQRBの面積がネックですね。直接求めることは出来ません。

表面積は
・底面と奥の正方形2枚(4×4)
・側面の台形2枚(上底2、下底4、高さ4)
・手前の三角形1枚(底辺4、高さ4)
・上部の五角形1枚(4×4の正方形から直角二等辺三角形2枚を切り取ったもの)
・切り口の三角形2枚
から構成されています。
底辺と高さが明らかでない切り口の三角形2枚の面積を求めます。
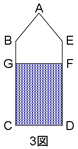
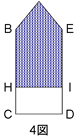
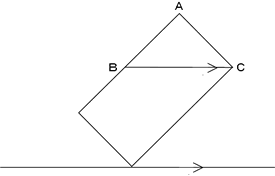
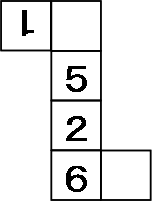
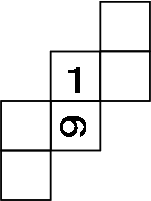
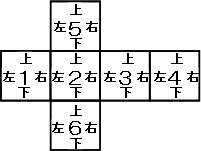
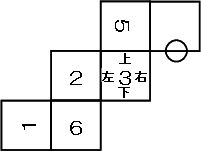
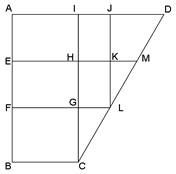
図は、立方体を真上から見た図です。
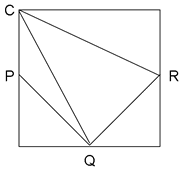
求めるべき切り口の三角形QRBと上部に作られる三角形QRCを比較する。
すると、
辺QRは二つの三角形に共通
QBとQCはともに正方形の一辺の中点から反対側の頂点に引かれた線であるため同じ長さ
RBとRCも同様
以上より三角形QRBと三角形QRCは、「3つの辺の長さが同じ」なので合同です。
もう1つの切り口の三角形PQAも同様。
よって切り口の2つの三角形の面積は、
上部に作られる三角形QRCの面積で代用します。
三角形QRCの面積は、
正方形(4×4)から直角三角形(2×4÷2)を2つと、
直角二等辺三角形(2×2÷2)
を1つ除いたものです。
よって面積は6平方センチメートル。
以上より
表面積は
底面と奥の正方形2枚:(4×4)×2枚=32
側面の台形2枚:[(2+4)×4÷2]×2枚=24
手前の三角形1枚:4×4÷2=8
上部の五角形1枚:4×4ー(2×2÷2)×2枚=12
切り口の三角形2枚:6×2枚=12
を合計して88平方センチメートル
答え:88平方センチメートル

昨年度の市川中の問題の中でも難問です。
切り口の三角形の面積については、誰もが着目し行き詰るでしょう。
ポイントは、
立体上の面積は、必ず平面にとらえなおすことです。
問題用紙に記載されている斜め上方からの図では、
感覚的にポイントとなる合同を見つけにくくなっています。
同じ長さの辺なども、そのような表記では違って見えるからです。
特に面積は相似、合同、比などの発見が突破口になります。
面倒くさがらずに面積問題として平面にする作業に取り組むことが大切です。
~今 回の問題から導かれる出題校からのメッセージ~
モデルの単純化が大切
立体ということで与えられた図だけを見ていても同様です。
そもそも立体であることは、
本問において惑わす要素にしかなっていません。
立体上の面積は、該当の部分を平面に書きおこすというのは定石ですが、
このように見た目に惑わされず本質のみを単純モデルとして考える思考法はとても大切です。
平面図形の面積の問題に取り組んでいるときは、
皆さん必ず相似合 同を考えるものですが、
立体上となるとと たんに頭の中から消えてしまうものなのです。
単純化することで、視界も広がり様々な方策が思い浮かびます。
トップクラスの生徒もこぞって受験する本校の最後の砦にふさわしい問題です。
合同に関しても三角形の合同条件がしっかり頭に入っていなければ
確信を持ちにくくしているところは、
平面に落とし込んだあとも確固たる力が求められる難問です。





![]()
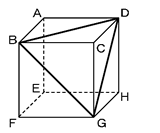
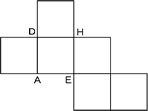
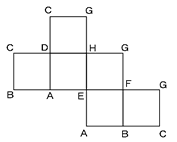
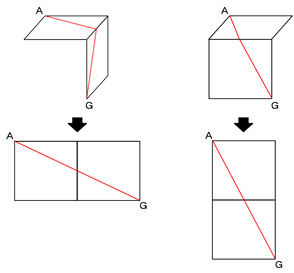
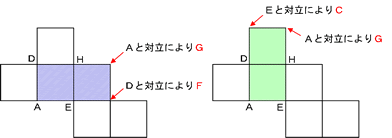
 図2
図2

 alt="" style="height: 188px; width: 234px;">
alt="" style="height: 188px; width: 234px;">