立体図形の問題を解くための大切な基本姿勢が問われます。

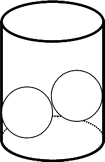
下の図1のような円柱の容器に、半径3cmの球を下の図のように2つ入れたところ、円柱の底から球の一番上までの高さが8cmとなった。そのままさらに球を入れていったところ、円柱の一番上のところで7個の球がちょうどおさまった。この円柱の高さを求めよ。

見方を変えてみましょう。

下の図1のように断面図で考えると中心から中心までの高さが2cmであることがわかる。
よって図2のように考えると求める高さは
図1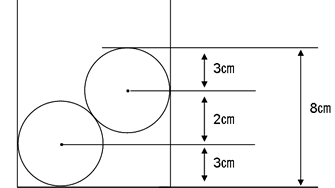 図2
図2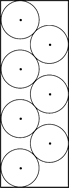
3cm+2cm×6+3cm=18cm
答え:18cm

見慣れない球という設定ですが、立体図形の基本は平面図形への分解です。
上から、横からなどに情報を分け、身近な平面図形として処理します。
難問としては、平面に落とし込んだあとに合同、相似などの平面図形の技術が要求されるものがあります。
立体図のままでは、合同、相似、補助線などの平面図形の知識を思いつき、活用することはとても難しいので、面倒でも平面図を書きおこすことが大切です。