地形図の読み取りとリード文の利用【対象学5年生以上】
地形図の読み取りとリード文の利用【対象学5年生以上】

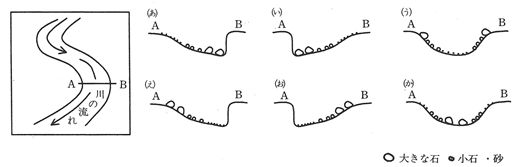
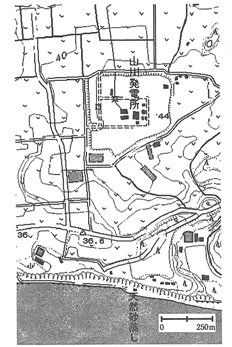
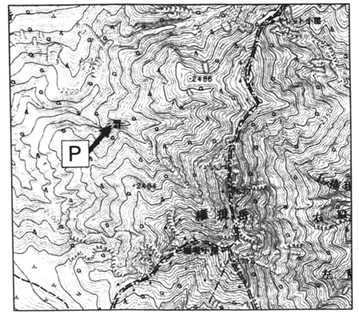
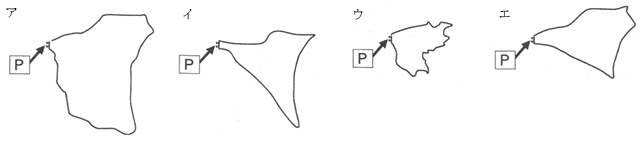
下の地形図は国土地理院発行2万5千分の1「八ヶ岳」の一部を拡大したものです。図中のPの滝での集水域として最も適しているものを、下の「集水域の見方とヒント」を参考にして、次のア~エから選び、記号で答えなさい。
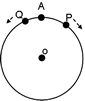
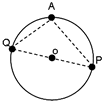
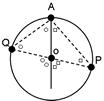
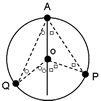
[集水域の見方とヒント] 集水域とは、水が集まってくる範囲をいいます。 左図のQのダムでは、Aの範囲が集水域です。 集水域を判断するには、右図のように地形図に描かれていない川(谷)に線を引いてみてもよく分かります。 これらの川を囲む尾根(山と山との頂を結んで続く最も高いところのつらなり)の部分に線を引いた範囲が集水域であることが分かります。
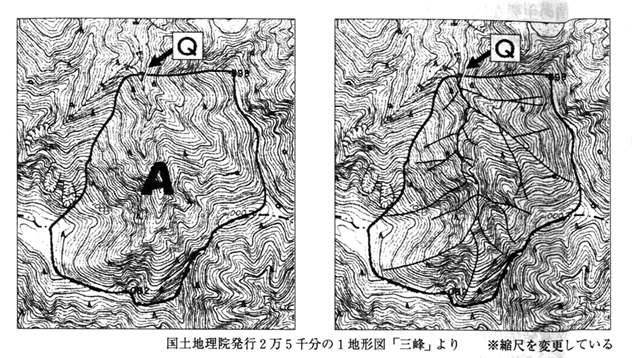

問題文のヒントがそのままヒントになります。
尾根と谷は等高線が、山頂にたいしてせり出しているか、へこんでいるかで見分けます。

ア

まず、尾根と谷とは何かを考えてみましょう。尾根とは山頂から続く山の高いところの連なりです。下の写真を見るとわかりますね。そして尾根と尾根に挟まれた部分はまわりより低くなった場所でそれを谷といいます。下の写真では手前の尾根Aと奥の尾根Bに挟まれた場所が谷になるわけです。
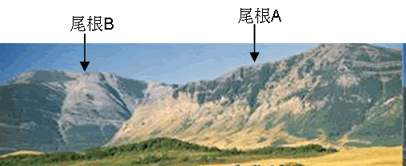
これを等高線で見ると、尾根の部分はまわりより高くなっていますから、山頂から、張り出す形になっています。また谷は、まわりより低いので、山頂に向かってへこむような形になることになります。
下図を見てみましょう。南東のはじにある赤い●がこの地域で最も高い場所です。そこから北に向かって、標高の高い数字が並んでいるので(下図の青い●)、それを結んだ線がこの地域で最も高い尾根ということになります(下図赤い太線)。
そしてその線を基準に等高線がはりだしている部分が尾根、へこんでいる部分が谷だということです。図の細い実線部分(尾根)や点線部分(谷)がそれに当たります。太い赤線より東側の部分にふった雨は東側へ、西側へ降った雨は西側へ流れるわけです。
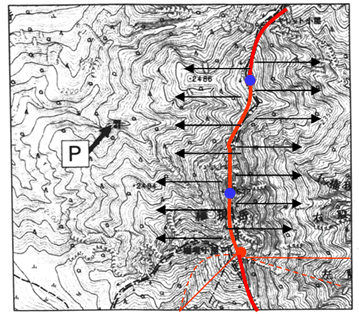
さて、では、問題文のヒントにしたがって、P地点の集水域を作図してみましょう。
P地点からそれより高い東側に向かって川の流れこむ谷を作図してみると、下図の太線AとBが谷になっていることがわかります。その二つの谷が、問題のヒントに与えられている川ということになります。(問題を解くだけなら不要ですが、その川に流れこむ周辺の川もいくつか描いておくと、より分かりやすくなります。(下図)
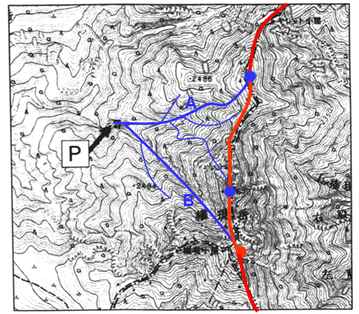
つぎに、問題のヒントにあるように、それを囲む尾根を探して、最初の太い赤線で描いた尾根までの線を引きます。
(下図)
すると、これがP地点の集水域だとわかりますから、アが正解となりますね。
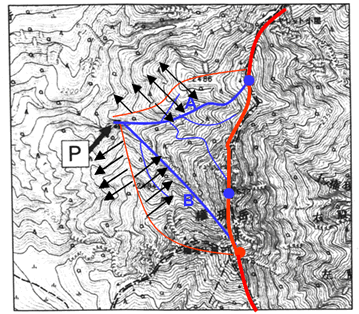
ちなみにこの集水域の境界に当たる尾根周辺では、降った雨は上図の矢印のように流れますから、作図が正しいことが確認できます。
集水域など、聞いたことがないし、やったことがない、と言っていても始まりません。問題文のヒントがある以上、それにしたがって、考えを進めていくことが大切です。
近年では、このような集水域を実際、作図させるような問題も出題されるようになってきました。非常に緻密で正確な思考と作業が必要な難問ですが、一度はやっておくとよい問題です。
--------------------------------------------------------------------------------
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー