「頂点決めの公式」

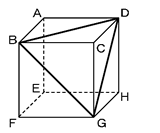
図1は、ある立方体をB、D、Gを通る平面で切ったときの切り口を表したものです。また、図2は、この立方体を切る前に展開したときの図です。図2の中に図1の切り口を書き入れるとどのようになりますか。

ありません。

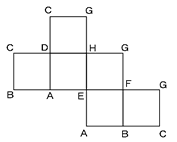

図1に表された切り口は、面ABCD、面BFGC、面CGHDの3つの面にあります。よって、図2の展開図に頂点を書き込んでいけばよいのです。頂点の決定のしかたには色々な方法がありますが、今回は「最も遠い2点」に注目してみます。
たとえば、Aから最も遠い点はGです。AからGへ隣り合う2つの面上を通って最短の道のりでいく場合、隣り合う2つの面を通る必要があります。これらを展開してみると、下の図のようになります。
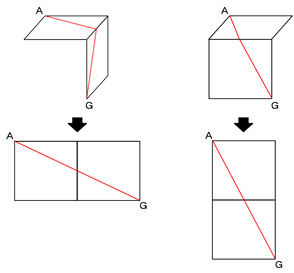
このように、立方体で最も遠い2点は、隣り合う2つの面を合わせた長方形でも最も遠い2つの点となるのです。これが、頂点決めの公式です。
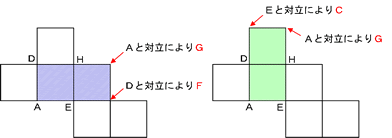
最も遠い2点の組み合わせはA-G、B-H、C-E、D-Fですから、下の展開図で青い長方形に注目するとAから最も遠い右上の点がG、Dから最も遠い右下の点がFと決められます。また、緑の長方形に注目すると、GとCが決められます。このようにして、隣り合う2つの面を合わせて考えると、ゲーム感覚(敵を探すように)ですべての頂点を決めることができます。
-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています~
1.
2.![]()
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー