女子学院中算数入試より。「複雑で身近なものに算数を使うための基本姿勢とは?」

1図のような、直方体と三角柱をつなげた形の五角柱の密閉された容器があり、下から15cmの 高さまで水が入っている。これをさかさまにして、水面と上の面が平行になるようにすると2図のようになる。
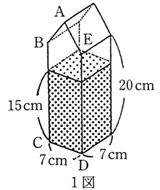
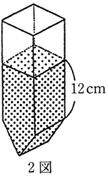
五角形ABCDの 面積を求めなさい。
(女子学院中)

さぼらず、求めたい部分の図 形を書き出して見ましょう。

面 ABCDEを底面として考えると、
水の容積は、1図において底面はCDFG、高さは7cmとして考える
ことができ、2図においては底面ABHIE、高さは7cmとできる。
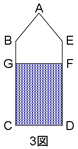
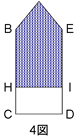
1図と2図で水の容積は同じ、高さはともに7cmであるから、
1図の底面である四角形CDFG(3図)と
2図の底面である五角形ABHIE(4図)
の面積は同じだということになる。
それゆえ、3図、4図の水と触れていない部分である
五角形ABGFEと
四角形HCDI
の面積も同じとなる。
よって求めるべき五角形ABCDEの面積は3図で考えると
五角形ABGFE+四角形GCDF となる。
五角形ABGFEの面積=四角形HCDI=7×8=56 平方cm
四角形GCDF=15×7=105 平方cm
よって
五角形ABCDE=56+105=161 平方cm
答え:161 平方cm

問題の図は、状況をすべて説明してくれる角度で描かれていますが、
これが問題の単純化を妨げています。
解答のような形で、求める平面図形をしっかりと把握することがもっとも大切です。
この視点で考えると、
五角形ABGFEの面積が超えなくてはいけないハードルであることが明らかになり、
方針が定まります。
今週の一問でも何度か取り上げていますが、
立体図形の単純化(=平面化)
はとても大切な技術です。
立体図形の中の面についてとりあげる問題は、
平面図形として考えればかなりやさしい問題でも、
立体の中に描かれたままでは、辺や角の関係を正確にイメージすることはとても難しくなります。
面倒でも書き出してみる几帳面さが求められます。
~今回の問題から導かれる出題校からのメッセージ~
基本的なモデルを考える視点が大切
女子学院中の算数は、
「基本的な問題をすばやく処理する能力が問われる」
と言われますが、いざ過去問を見てみると、
教科書や基本問題集では見たことのないような図形、設定がほとんどです。
本校の問題の特徴は、
「超基本的な算数技術を、身近な題材に対して適用させる。」
ことです。
身近な題材とは、
「具体的な容器に入った水」「点ではなく人や乗り物の移動」「数の計算ではなく値段の計算」
など生活に密着してはいますが、算数の題材としては極めて数値化しにくいものです。
このようなタイプの問題に取り組むなかで、普段から
「これはそもそもどの算数の技術が問われているの か」
について検討する習慣をつけておくことが大切です。
さもなければ問題の本質とは関係のない設定に振り回されて終わってしまいます。
ほとんどの生徒にとって、算数・数学はそのもののために勉強するのではなく、
実生活で出会うものを計算、測量するためのものです。
複雑な対象を、計算可能な形に落とし込む工夫を求める本問は、
高い学識を活かし実社会で活躍する人材を輩出する本校の指導方針を反映した良問です。