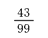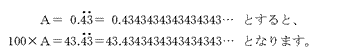学習塾ロジム　今週の1問by 学習塾ロジム

数列の利用【対象学年：４年生以上】

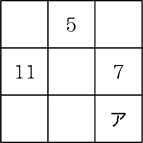
下の数列は
１，１，２，３，５，８，１３，２１，３４，・・・
「前の２つの数を加えると次の数になる」という数列です。


この性質に似た性質がかくれている問題が直線の本数とその交点の数です。
直線に対してできるだけ多くの交点を作った場合

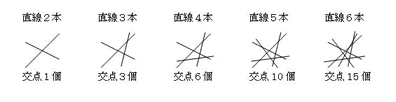
と交点が増えていきます。

（１）７本目の直線をひいたとき６本目のときより何個交点は増えますか。
（２）直線が８本のときの交点の数は何個ありますか。
（３）100本目の直線をひいたとき99本目のときより何個交点は増えましたか。

　直線の本数と交点の数、そして「前の２つの数を加えると次の数になる」ことを意識して考える。



























(1)６個
(2)28個
(3)99個

(1)数本の直線に対して新しく１本の直線を引いた場合、その数本の直線の1本につき１つの交点が新しくできます。
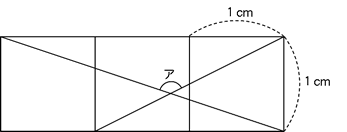
例えば、３本の直線に対して新しく１本の直線を引いた場合は下の図のようになります。

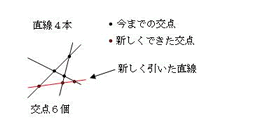
３本の線に対して、１本の直線を引くことにより、その３本に新しく交点が１つずつできます。よって、６本の線に対して７本目の直線を引くと新しく６個の交点が増えることになります。

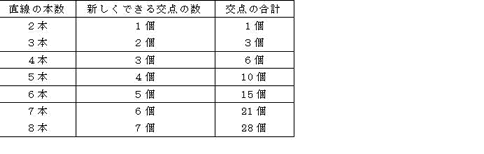
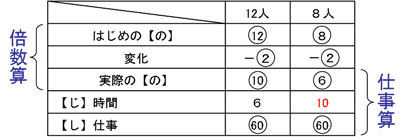
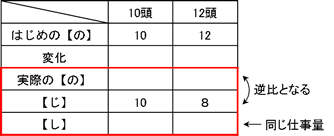
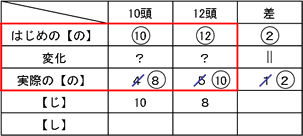
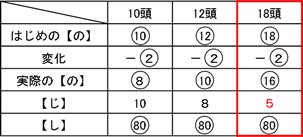
手前の本数の数と交点の数を足すと次の交点の合計になっていることがわかります。

(3)上の表より新しくできる交点の数は、１つ手前の直線の本数と等しくなっていることがわかります。よって、100本目の直線の交点はそれまでの99本の直線と交点をつくるので99個になります。

--------------------------------------------------------------------------------

参考書選びの参考にご利用ください。

ロジム2階参考書コーナー

倍数に注目しよう　【対象学年：5年生以上】



345は３で割り切れます。

1473は３で割り切れます。

857421は３で割り切れます。



このとき、

345の各位の和は３＋４＋５＝12

1473の各位の和は１＋４＋７＋３＝15

857421の各位の和は８＋５＋７＋４＋２＋１＝27

となり、それぞれ３の倍数となっています。



次の問いに答えなさい。



(１)下記はなぜ各位の和が３の倍数であれば３で割り切れるのかを説明した文章です。

　　空欄に入る数をいれなさい。



1473を、各位に分けて式で表すと、

１×1000　＋　４×100　＋　７×10　＋　３

となります。

次に、式をわけると次のようになります。
１×［ ア ］＋１　＋　４×［ イ ］＋４　＋　７×［ ウ ］＋７　＋　３

とすると、各位の数を１個ずつ集めることが出来ます。
１×［ ア ］　＋　４×［ イ ］　＋　７×［ ウ ］　＋　１＋４＋７＋３

これを、それぞれ３で割れば下の式のように
（１×［ エ ］　＋　４×［ オ ］　＋　７［ カ ］　＋　［ キ ］）×［ ク ］
とまとめることが出来ます。
よって、各位の和が３の倍数であれば３の倍数といえます。

同じ考え方で［ ケ ］の倍数も説明できます。

７×５は７が５つと考えると、７×４＋７と表せます。



























ア　999
イ　99
ウ　9
エ　333
オ　33
カ　3
キ　5
ク　3
ケ　9







１×1000　＋　４×100　＋　７×10　＋　３をそれぞれ、
１×999＋１　と　４×99＋４　と　７×９＋７　と　３　
にわけることがポイントです。
こうすることで、１×999と４×99と７×9は３
そして、残った１＋４＋７＋３(各位の和)が３の倍数であれば全ての数が３で割り切れるといえますね。

ケについても１×999と４×99と７×9は９の倍数といえるので、残っている各位の和が９の倍数であれば、９で割り切れるといえます。

--------------------------------------------------------------------------------

参考書選びの参考にご利用ください。

ロジム2階参考書コーナー

　平均魔法陣。





　次の魔方陣（たて、横、ななめそれぞれ３つの数の和が等しい）を完成させたとき、アにあてはまる数はいくつですか。

　すでにうめられている数と場所に秘密があります。

　８

　まず、数の入っていないマスにそれぞれイ～カの記号を入れておきます。
下の図のように１列の合計３つ分を比べると、ア×２＝５＋11とわかります。よって、ア＝８となります。

　つまり、アは５と11の平均だったということになります。
このように、１つのマスを３回ダブらせるようにして比べると、ダブったところは合計にふくんでいない数の平均ということになりますね。
　たとえば、オは５と７の平均です。また、エは７と11の平均です。

-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています～

1.

2.
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー

　２・２・３の直角三角形。





　下の図は、１辺が１cmの正方形を３つ合わせたものです。この図で、角アの大きさを求めなさい。

　見えない角度を作ります。

　135度

　まず、合同な直角三角形を下の図１のように向きを変えてならべると、間に直角があらわれます。
このことから、正方形をしきつめた図形の中には、見えない直角があらわれます。その一例が、正方形を６つしきつめたときの「２つ・２つ・３つの正方形の対角線」でできる直角三角形です。

　この問題も、図２のように６つの正方形をつくることで新たに直角二等辺三角形をつくることが可能です。
このパターンは頻出なわりに、意外にも正答率は高くありません。

　また、これと似た問題で、正方形（親）の中にできる傾いた正方形（子）も頻出ですね。

-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています～

1.

2.
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー

　2010年度入試シリーズ　(2)早稲田中学校【理科】より

　最近、発光ダイオード（ＬＥＤ）という明かりがいろいろなところで使われるようになってきた。
ＬＥＤにはつなぐ向きがあって、図１（ａ）のように正しい向き（順方向）につなぐと電流が流れて光るが、図１（ｂ）のように逆向き（逆方向）につなぐと電流が流れずに光らない、という性質を持つ。

　いま、図１（ａ）と（ｃ）のようにＬＥＤと豆電球をそれぞれ同じ電池につないだところ、ほぼ同じ明るさで光った。豆電球をつないだときに回路に流れる電流は200mAであった。
　次に、図２のようにこれらの豆電球とＬＥＤを並列につないで、先ほどの電池につないだ。このとき電流計は220mAを示した。

問１　図２のように並列につないだ場合、ＬＥＤと豆電球の明るさはどうなるか。以下から選び、記号で答えよ。
　　ア　豆電球のほうが明るい　　イ　ＬＥＤのほうが明るい　　ウ　ほぼ同じ明るさである

　　電流の基本です。

　ウ

　ＬＥＤの問題は、中学入試理科の常連となったと言っても過言ではありません。
それほど近年毎年出題されていますが、それらの多くは「順方向・逆方向のつなぎ方による回路作り」でした。電流が流れる道をきちんと精査し、つなぎ方を条件に合うように変えるものですが、本問は一風変わった出題となっています。
豆電球の学習における「電流が大きいほうが明るい」という常識からはなれることができなければ、受験生も混乱してしまったのではないでしょうか。

　まず、図１の（ａ）と（ｃ）から、乾電池１個分の電圧をかけることでほぼ同じ明るさで光ることがわかります。
図２のように並列につないだ場合にも、豆電球とＬＥＤにはそれぞれ乾電池１個分の電圧がかかることに変わりはありませんから、当然ほぼ同じ明るさで光ります。

　しかし、問題文の「次に、・・・」以降によって、混乱させられた受験生は多いはずです。図２の電流計は220mAを示しています。豆電球のほうには200mAの電流が流れているはずですから、ＬＥＤのほうには20mAしか電流が流れていません。ということはＬＥＤのほうが暗い・・・？という混乱です。電流の大きさで明るさを比べる習慣があると、逆に混乱してしまうでしょう。並列回路だから、かかる電圧が等しいという「電流の基本」が問われています。

※ちなみに、ＬＥＤは小さな電流で明るく光ることができる装置です。

-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています～

1.

2.
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー

　2010年度入試シリーズ　(1)桐朋中学校【算数】より

　ある遊園地では、午前10時に入場券を売り出します。午前10時に窓口にはすでに180人が並んでいました。その後、行列には毎分３人ずつの割合で人が加わります。午前10時に１つの窓口で入場券を売り出したら、午前11時20分に行列がなくなりました。もし、午前10時に２つの窓口で入場券を売り出したら、行列は何時何分になくなりますか。

　　ニュートン算の基本です。

　10時24分

　非常に基本的なニュートン算ですが、前回ニュートン算が表で解けることを紹介したので、せっかくですから入試問題を表で解いてみましょう。
まず、並んでいる180人をなくすわけですから、
全体の仕事の量が180であると考えられます。
窓口が１つの場合80分で仕事が終わり（行列がなくなり）ますが、毎分３人ずつ並んできてしまうため、
能力（１分でこなせる仕事）は３減らされてしまいます。これらを、表に整理すると下の黒字ようになります。

　これより、実際の能力（仕事の速さ）は180÷80＝2.25となり、はじめの能力は5.25とわかります。窓口１つの能力が5.25ですから、窓口２つのときのはじめの能力は5.25×２＝10.5です。よって、窓口２つのときの実際の能力は10.5－３＝7.5ですから、これを表の中にうめていくと、上の青字になります。
　以上より、求める時間は180÷7.5＝24となり、開始が10時なので10時24分となります（赤字）。

-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています～

1.

2.
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー

「ニュートン算＝倍数算＋仕事算」と、気づいていますか？

　ある牧草地で、牛10頭を放しておくと10日で草を食べつくしてしまいます。また、この牧草地で、牛12頭を放しておくと８日で草を食べつくしてしまいます。
では、この牧草地で、牛18頭を放しておくと草をたべつくすのに何日かかりますか。
ただし、この牧草地は一定の割合で草が生え続けています。

　増加と減少が同時に起こる、いわゆるニュートン算です。

５日

　　さて、ニュートン算が難しいと感じられる点はどこでしょうか・・・？

それは、「増加と減少が同時に起きている」という点に加え「増加と減少のうち一方は個数に比例するものの、他方は個数に関係なく絶えず一定である」という点に他なりません。

その点を単純化してある問題が、いわゆる仕事算です。

「12人ですると６日で終わる仕事を８人ですると何日か？」
実際に行う仕事は人数に比例しますから、１人で１日にする仕事の量を１とすれば、全体の仕事量は12×６＝72となり、これを８人で行うので72÷８＝９日とわかります。

　しかし、ここで絶えずこの仕事が１日に増えていくことを考えます。

例えば、仕事を行う人数に関係なく、毎日仕事が２ずつ増えていくとしましょう。
すると、12人では１日に12の仕事を行いますが、２だけ増えてしまうので結果として12－２＝10しか仕事をすることができません。
また、８人の場合も同様に１日あたり８－２＝６しか仕事をすることができなくなってしまうのです。
これにより、実際に12人で行う仕事の量は（12－２）×６＝60となり、これを８人で行うとすれば60÷（８－２）＝10日となるのです。

このように、一見複雑そうなニュートン算ですが、仕事算のように表に整理してみると簡単です。上３段が能力（仕事の速さ）の変化についての倍数算、そして下３段が実際の能力での仕事算となっているのです。

では、ニュートン算の仕組みがわかったところで、本題を解いてみましょう。
まず、表に整理すると下のようになります。

同じ仕事（草を食べること）をするのに、10日と８日かかっているわけですから、実際の【の】はその逆比となり４：５であることがわかります。これにより、はじめに10：12だった能力が、同じ分だけ減って４：５になっているので、一定である差で比をそろえます。これにより、牛１頭あたりの能力が１で、変化が－２であることがわかります。

全体の仕事が８×10＝80とわかるので、同じようにして牛18頭の場合を考えてみます。実際の能力は18－２＝16となり、80÷16＝５日と求められます。

-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています～

1.

2.
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー

循環小数

　次のように、小数で表すと無限に続いてしまう小数を「無限小数」といいます。

　特に、同じ数字のかたまりがくり返しあらわれるものは「循環小数」といい、くり返しの部分のはじめとおわりに・をつけて表します（１つの数字がくり返される場合は・１つです）。

　これをもとに、循環小数0.4343434343434343・・・・・を分数で表しなさい。

　無限に続く部分を「消す」必要がありますね。

　まず、無限に続く小数部分を消去するために、くり返しあらわれる周期を利用します。

　これより、差をとることで小数部分が消え、99×Ａ＝43と表せるのです。

-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています～

1.

2.
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー

　複雑な回路を流れる電流

　下の図のように、豆電球３つと乾電池２つとスイッチ３つを使って回路をつくりました。いま、Ａ～Ｃのスイッチはどれも入っていませんが、アとウの豆電球が光っていました。これについて、次の問いに答えなさい。

(1) Ａのスイッチだけを入れると、ア～ウのうちどの豆電球が光りますか。

(2) すべてのスイッチを入れると、ア～ウのうちどの豆電球が光りますか。

　電流の気持ちになってください。

(1) ア、イ、ウ
(2) イ、ウ

　まず、電流が流れるルールを確認しましょう。
豆電球は電気抵抗なので、豆電球が多ければ多いほど電流は流れにくくなります。特に、豆電球を並列につないだ場合、それぞれを流れる電流の大きさは豆電球の個数の逆比になります。

　たとえば、豆電球１個と２個を並列（道が分かれている状態）につないだ場合、流れる電流は２：１となるのです。
このことから、下の図のように、もしも分かれた道の一方に豆電球がなかった場合、豆電球のある方へ流れる電流が０となり、すべての電流が豆電球のない道を選んで流れることになります。

　このように、複数のスイッチや並列部分をふくむ複雑な回路では、どこを電流が流れるのか（どこを電流が流れないのか）をきちんと調べることが重要です。この際にポイントとなるのが「道が分かれたら再び合流する位置を探し、それぞれの道で豆電球がない道があればそこしか電流は流れない」ということです。

(1) まず、説明のために、図１のように各地点を「あ」～「お」とします。
電池を出た電流は「あ」で道が分かれます。このとき、「い」へ向かう電流と「え」へ向かう電流が合流する地点は「お」しかありません。
このとき、どちらの道にも豆電球があるので、どちらも流れることになります（流れる電流の大きさの比は、１：２ですね）。

(2) 図１と同様に「あ」～「お」とします。電池を出た電流は「あ」で道が分かれます。
このとき、「い」と「う」と「え」に向かって電流が流れていきます。
ここで、次の３つの場合を考えてみましょう。

１．「い」で合流する場合・・・「あ－い」の間は流れません（この道だけ豆電球があるため）。
２．「う」で合流する場合・・・「あ－い」の間は流れません（この道だけ豆電球があるため）。
３．「え」で合流する場合・・・「あ－い」の間は流れません（この道だけ豆電球があるため）。

　よって、どこで合流するにせよ、「あ－い」の間を通らなくてすむ道があるので、「い」に向かっては流れないことがわかります。
「う」と「え」に分かれて流れた電流は、このあと「お」で合流することになりますが、この場合どちらも豆電球があるのでどちらにも流れることになります。

では、スイッチＡとＢのみを入れた場合はどうなるでしょう？
ぜひ、考えてみてください。

-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています～

1.

2.
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー

　合わせ鏡の公式

　図のように、２枚の鏡をある角度で合わせ、中央にろうそくを置いたときにいくつの像ができるかを調べたところ、結果は表のようになりました。これについて、次の問いに答えなさい。

(1) 表の結果から、できる像の個数は次のような式で求めることができます。次の式の空欄に、あてはまる数を答えなさい。

(2) 鏡の角度が30度のとき、像は何個できますか。

　ありません。

(1) ア　360　　イ　１
(2) 11個

　１つの例として、90度の場合を考えてみます。
下の図のように、２枚の鏡をＡ、Ｂとすると、Ａに映ったＢ、Ｂに映ったＡというようにして、新しく鏡Ｃ、Ｄができたと考えることができます。
これにより、鏡Ａ、Ｂでできた像が、鏡ＣやＤでもできるので、その像の個数を考える必要があります。

　この場合、はじめの鏡の角度が90度であることから、下の図のように360÷90＝４で、鏡や鏡の像によって４つの場所に区切られます。
ここにそれぞれ像ができますが、その場所のうち１つは実際の物体（ろうそく）がいることになるので、像は４－１＝３個となるのです。

　同じようにして、例えば鏡の角度が60度の場合、360÷60＝６で、鏡や鏡の像によって６つの場所に区切られます。
このうち１つは実際の物体（ろうそく）がいることになるので、像は６－１＝５個となるのです。

　つまり、合わせ鏡による像の個数は「360度÷鏡の角度－１」で求められるのです。

-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています～

1.

2.
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー