サイコロの塗りわけ【対象学5年生以上】

1から6までの数字がかかれたサイコロがあります。6色の絵の具を使い、隣り合う面が違う色になるように塗り分けます。全部で何通りの塗り方がありますか。6色すべてを使う必要はありません。

使う絵の具の種類によって場合わけしていきます。

4080通り

(i)3色で塗り分ける場合
1と6,2と5,3と4を同じ色にします。
1と6の塗り方は6通り,2と5の塗り方は5通り,3と4の塗り方は4通りなので6×5×4=120通り
(ii)4色で塗り分ける場合
まず、1と6,2と5,3と4のうち2組を選んで2色使います。そして残りの2面に使っていない4色のうちから1色ずつつかいます。
選ばれた2組をAとB,残りの2面をCとDとすると塗り方は6×5×4×3=360通りです。
AとBの選び方は,1と6,2と5,3と4の3組から2組選ぶので3通りあります。よって4色で塗り分けるのは360×3=1080通り
(iii)5色で塗り分ける場合
まず、1と6,2と5,3と4のうち1組を選んで1色使います。そして残りの4面を4色で塗り分けます。
選ばれた1組をA,残りの4面をB,C,D,Eとすると塗り方は6×5×4×3×2=720通りです。
Aの選び方は,1と6,2と5,3と4の3組から1組選ぶので3通りあります。よって5色で塗り分けるのは720×3=2160通り
(iv)6色で塗り分ける場合
6×5×4×3×2×1=720通り
以上より合計4080通り
場合の数に関する基本事項が全て含まれている良問です。
和の法則,積の法則,そして「まず枠組みのパターンを決定して,塗り分けを考える」という手順です。
解答の(i)~(iii)にあるように,まず「どことどこを同じ色にするか」ということが先決です。下の図のような地図の塗り分け問題は見たことがあるのではないでしょうか。
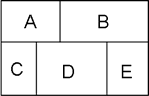
この場合も,まずどことどこを同じ色にするかを決定します。4色で塗り分けるなら、AとEを同じにするかBとCを同じにするかCとEを同じにするかのパターンがありますね。
さらに場合の数の応用として,「回転させて同じになるものは1通りと考える」というものがあります。
本問をサイコロではなく,数字の書いていない立方体と考えて「6色すべてを使って塗り分けるのは何通りか。」を考えてみてください。
--------------------------------------------------------------------------------
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー