ダイヤグラムの間違いを見つける【対象学5年生以上】

太田くんは自分の家から分速60mの速さで駅まで歩くことにしました。
しかし、30分歩いたところで忘れ物に気づき分速100mで忘れ物を取りに帰り、帰ったときの速さで駅まで向かいました。すると、予定より32分遅くなってしまいました。
太田くんの家から駅までは何m離れていますか。
この問題を以下のダイヤグラムにしました。
しかし、以下のダイヤグラムには誤りがあります。
このダイヤグラムの誤りを指摘し、正しいダイヤグラムを完成させ太田くんの家から駅までの道のりを求めなさい。
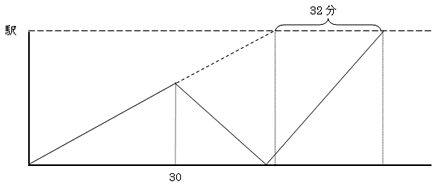

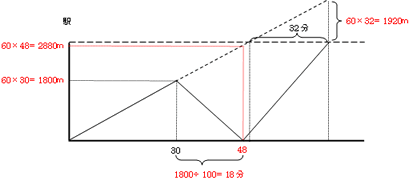
2880m離れている状態から追い越しの旅人算となる。1920m離れている状態になるまでは、2880-1920=960m近づく必要がある。よって、近づくためには960÷(100-60)=24分かかります。48分の地点から32分以上後に駅に着く予定ですが、24分後に1920mはなれた状態(分速100mで駅に着いたとき)になると考えると矛盾が起きます。
このことより、ダイヤグラムが誤っていることがわかりますね。

(誤りの指摘)ヒントを参照
(正しいダイヤグラム)
忘れ物を取りに帰っている途中に駅に分速60mが駅に着いている状態。
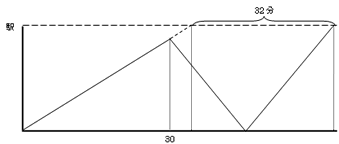
(道のり)2400m

家から駅まで分速60mで歩き続けた場合と、忘れ物を取ってから駅まで行った距離は同じです。そのときの速さの比は(60:100)=3:5となるのでかかった時間の比は5:3となります。この時間の比を⑤と③とします。
すると、下の図のようにまとめることができます。
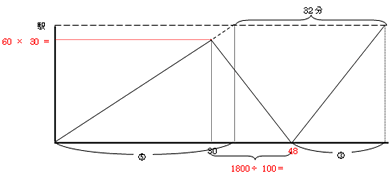
上の図より、
⑤+32(分)=48(分)+③となることがわかります。
②=16分
①=8分
③=24分
となるので、分速100mで24分走るとつく距離だということがわかります。
よって、家から駅までは100×24=2400mとなります。
--------------------------------------------------------------------------------
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー