思う存分、引っかかってください。2009-02-16 (訂正あり)
思う存分、引っかかってください。

解答・解説に誤りがございました。赤字箇所訂正させていただきます。大変ご迷惑おかけいたしました。
---------------------------------------------
下の図は、ある日に太陽が西の地平線に沈み始めたところを表しています。この状態から、完全に地平線の下にかくれるまで2分30秒かかりました。図中の矢印は、太陽の沈む方向を表しています。また、三角形EFGでFG:EF:EG=3:4:5で、Eは太陽の中心を表しています。これらのことから、太陽の大きさを地球から見たときの角度(これを視直径といいます)で表すと何度になりますか。
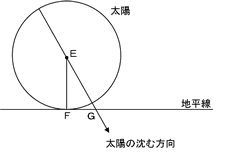

視直径は、長さではなく「角度」です。


「完全に地平線の下までかくれるまで」とあるので、とりあえず図示してみると、下の図のようになります。
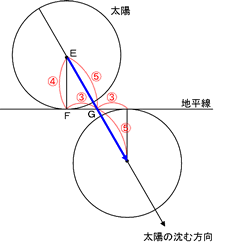
これから、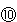 進むのに2分30秒(150秒)かかったことになりますから、
進むのに2分30秒(150秒)かかったことになりますから、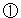 あたり15秒かかることになります。EFが
あたり15秒かかることになります。EFが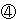 で表されることから視直径は
で表されることから視直径は ですから、太陽が120秒(2分)で進む大きさということになります。
ですから、太陽が120秒(2分)で進む大きさということになります。
ここで、太陽は地球の自転により1日に360度回転して見える(これを日周運動という)ので、1時間あたり15度→1度あたり4分→2分あたり0.5度となります。
さて、この問題では次のような誤答(勘違い)が多く見られたと考えられます。
■「完全に地平線の下までかくれるまで」に太陽が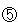 進んだと捉え間違えた場合
進んだと捉え間違えた場合
これは、きちんと自分の手で太陽が沈んだ状態を図示しないために起こるものです。
複雑な問題こそ、面倒くさがらずに与えられた条件等を図示して整理したいものです。
■太陽の日周運動において、1分あたり4度進むという勘違いをした場合
これは、あいまいな記憶と焦りが導いたものです。
実際、多くの受験生に「1度で何分?」と問うと「4分」という正答が得られる一方で、
「1分で何度?」と問うと「4度」という誤答が目立ちます。
■「視直径」を強く意識しなかった場合
解説の図のとおり、EF=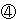 を利用するというところまでわかればあとはさほど難しくありません。しかし、問われていることが視直径である(図の太陽の直径を表している)ことをイシキしておかないと、そのまま
を利用するというところまでわかればあとはさほど難しくありません。しかし、問われていることが視直径である(図の太陽の直径を表している)ことをイシキしておかないと、そのまま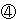 を用いてしまい、0.25度という誤答を導き出してしまいます。ちなみにこれでは、視「半径」ですね。
を用いてしまい、0.25度という誤答を導き出してしまいます。ちなみにこれでは、視「半径」ですね。
-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています~
1.
2.![]()
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー