ひっかかりやすい積み木の個数【対象学年:4年生以上】

下の図1は、小さな立方体をいくつか使ってつくった立体を、正面、上、右からそれぞれ見た図です。この場合、最も少なくて6個、最も多くて8個の立方体で作ることができます。
では、図2のように見えるようにするには、最も少なくて何個の立方体が必要ですか。
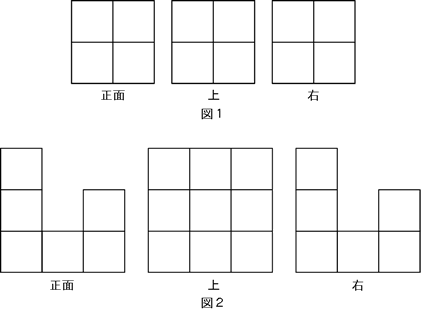

上から見た9か所すべてに立方体は必要でしょうか?

11個

まず、図1が6個~8個でできることを考えてみましょう。
上から見た図の中に、正面、右から見た(積み上がった最大の)立方体の情報を書き込んでみると、次の図のようになります。
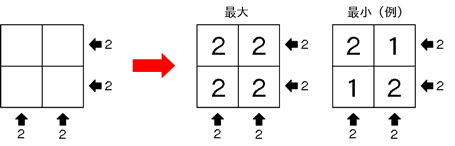
さて、図2の場合を考えてみます。同じように、上から見た図の中に情報を書きこむと次のようになります。説明のために、ア~ケと名前をつけておきます。
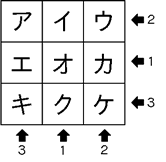
まず、1個しか積み上がって見えない「イ・オ・ク・エ・カ」は1個と考えられます。また、最大である3個積み上がっている場所はできるだけ少ない方がよいわけですから、「キ」が3個と考えられます。同様に、2個積み上がっている場所もできるだけ少ない方がよいわけですから、「ウ」が2個と考えれらます。
残った「ア・ケ」はあればよいわけですから、1個と考えられます。以上より、全部で12個となります。
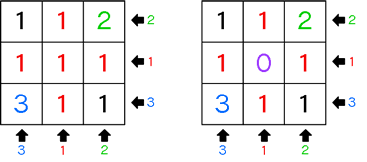
しかし、実はこれは最小の個数ではありません。図のオをつくる4辺は、まわりに立方体がありさえすれば存在しますから、実はオは0個で構いません(オ意外の場所は、まわりに囲まれているわけではないので、そこに立方体がないと4辺ができあがらないため、1個以上必要になります)。
以上より、本当の最小の個数は11個となります。
-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています~
1.
2.![]()
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー