今週は、算数分野からの一問です。

ある階段があります。
まさるくんは1段ずつとばして、たけしくんは2段ずつとばして登りはじめました。
すると一番上の段まで、ふたりともその歩幅のまま、ちょうど登りきりました。
登りきるまでの2人の歩数のちがいが14歩だったそうです。
この階段は一体何段だったのでしょう。
(雙葉中改題)

ノートに階段の絵を書くことからはじめてください。問題とにらめっこしていても何も
進みません。「まず手を動かす」、重要な習慣です。

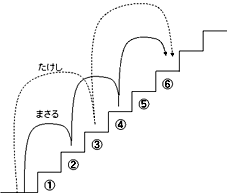
下の図のように、2と3の公倍数である6段目でちょうど1歩の差がつくことがわかる。
つまり6段ごとにちょうど1歩差がつく。
二人ともちょうど登りきり、歩数の差が14歩だったので、
階段は6×14=84段だということがわかる。
こたえ, 84段

この問題から、考えるべきことは以下の2点です。
┏━━━━━━━━━━━━━━━━━━━━━┓
1.単位に対するの注意力・意識力
2.起こっている事象をイメージし、図示する力
┗━━━━━━━━━━━━━━━━━━━━━┛
解答を見る限り、とても簡単な問題です。
実際、4年生のクラスでも半数以上が1分以内に答えをだすことができました。
しかし、この問題の誤答例は、とても重要なことを気づかせてくれるものです。
試験当日も含めて、不正解の解答のほとんどは、
「3-2=1 14÷1=14 14×2=28段」 もしくは
「3-2=1 14÷1=14 14×3=42段」の
どちらかになりました。
つまり、
「1回の行動で二人の差は1。そして最終的に差は14。
つまり14回同じ行動が繰り返された。1回につき2段(たけしくんを基準とした場合は3段)
進むので2×14=28 (たけしくんを基準とした場合は3×14=42)」
という論法です。
この誤った論法に陥っている原因は、
1. 差の単位について「歩」と「段」を混同もしくは無視している。
2. 解答の図のような具体的なイメージをしていない。
に集約されます。
この問題は、「歩く」ことによる「差」は、まず「距離」か「時間」だと
決めつけがちな生徒たちに、
「問題文を読みながら『具体的なイメージ』を描こうとしていますか、
そして『単位』に敏感になっていますか」
と問うているのです。
この問題は、6年生の上位クラスの教室でも上記のような誤答が散見されます。
解くスピードを重視するあまり、式のみで論を進めようとすることが
「具体的なイメージ」をつくることを省略させ、
単位のない式のみの展開に陥らせるのです。
本当のスピードは「具体的なイメージ」によって加速されます。
そして、単位の意識こそがその「具体的なイメージ」を助けてくれます。
正答者の8割以上が解答のような図を描いて考えています。
また不正解者で、図を描いた生徒は0でした。
「ちょっと絵と日本語で説明してもらえる?」という問いかけで、
お子様の思考の癖が垣間見ることのできる良問です。