本当の学習とは、教わる学習ではなく「自ら歩み出す学習」です。

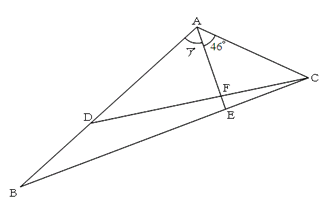
下の図で、ACの長さは10cm、AFの長さは6cmで、(ADの長さ):(BDの長さ)=3:2、(BEの長さ):(ECの長さ)=5:2であるとき、図のアの角度は何度ですか。

・平行線の威力を感じてください。
・気づく必要はありません。色々と試してください。

67度

図1のように、与えられた情報を書き込むと、ABとBEが異なる比ながらも「5」で揃います。
図1: 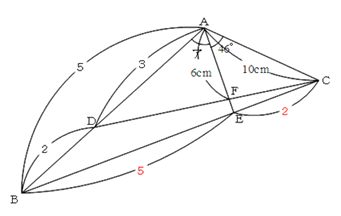
平行線にそって比が移動できる(相似の性質─ピラミッド)を利用すれば、図2のように新たに点Gを作ることで点Dを頂点とした新たなピラミッドが出来あがります。
図2: 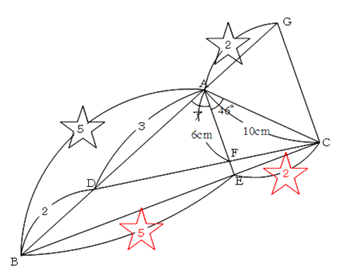
このとき、三角形DAFと三角形DGCが相似であること(相似比3:5)から、
辺CG=6×(5/3)=10cm
とわかります。
つまり、△CAGは二等辺三角形となります。
さらに、AFとGCが平行ですから、平行線の錯角を利用して
角AGC=46度となり、
角CAG=角CGA=(180-46)÷2=67度
とわかります。
求める角アは、平行線の同位角によって角CGAと等しくなるので、答えは67度となります。
-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています~
1.
2.![]()
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー