「固定」の威力を感じてください。

長さ3㎝の棒ア、イと長さ4㎝の棒ウがつながってできたものを机の上におきます。図1は、これを真上から見たものです。また、棒どうしは図2や図3のように、連結部分A、Bで折り曲げることができますが、棒と棒の間の角度を90度より小さくすることはできません。
棒のはしを下の図1のようにX、Yとし、棒アのみを机の上に固定したとき、棒ウの先Yの動くことのできる部分の面積を求めなさい。ただし、棒の太さや連結部分のすき間を考えないものとします。
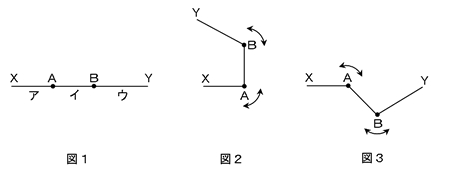

とりあえず、点Yの動く範囲を図示しなければ始まりません。

37.68(平方cm)

まず、対称性を利用すれば、下側に曲げた場合のみを考え、その面積を2倍することでもとめる面積がわかります。ここで、棒イを固定して棒ウを動かすと、点Yは下の図Ⅰのような四分円の弧YY’を描きます。そして、棒イを回転させることで、図ⅡのようにYとY’の行き先がわかります。よって、点Yの動くことのできる範囲は、下の図Ⅲのようになります。
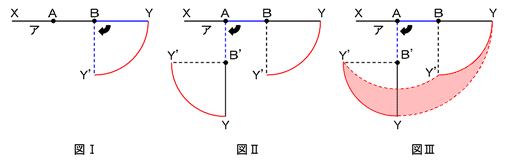
実際、面積を求めにいくときには、この複雑な図形がどのような簡易な図形(三角形やおうぎ形など)が組み合わされてできているのかを考えていきます。
ここで、下の図Ⅳのように点Y’が動いて描いた弧YY’は点Aを中心とした四分円の弧なので、半径はAY’となります。三角形ABY’はAB=3㎝、BY’=4㎝の直角三角形なので、AY’=5㎝です。
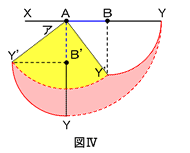
これより、求める面積は、以下のようにして求められます。
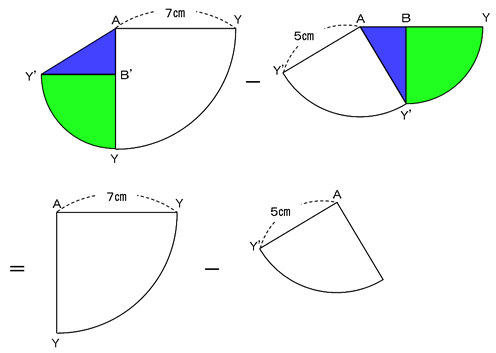
よって、(7×7-5×5)×3.14÷4=6×3.14となり、
対称性から、6×3.14×2=12×3.14=37.68(平方cm)とわかります。
このように、変化するものが2つ以上ある「複雑な動き」を考える場合、闇雲に動かす(試す)だけではなかなか正確に全体像をつかむことができません。場合の数などと同様に、1つを固定して考えるだけで、一気にわかりやすくなることは少なくありません。
-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています~
1.
2.![]()
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー