隠れた制限を考えます【対象学年：5年生以上】
全体の人数が100人以上、200人未満の学校があります。
この学校の生徒を通学地域別のＡ、Ｂ、Ｃ、Ｄ、Ｅの5つのグループに分けたら、次のようになりました。
（1）Ａの人数はＢの人数の1.2倍
（２）Ｃの人数はＢの人数の1.4倍より3人少ない
（３）Ｄの人数はＣの人数より5人少ない
（４）Ｅの人数はＡの人数より1人多い
条件を満たすＢの人数は何通り考えられますか。
（芝中）
分数で考えてみましょう。
（1）より
Ａ対Ｂ＝1.2:1＝6:5
よって、Ａの人数は6の倍数、Ｂの人数は5の倍数となる。
（2）より
Ｂ：Ｃ+3＝1:1.4＝5:7
Bを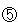
とすると、Ａは
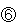、Ｃは
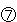-3人、Ｄは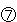-3人、Ｅは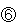+1人
合計は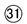
－10人
よって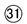が110人以上210人未満となる。
これを満たす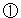
は4人、5人、6人の3通り。
よってＢの人数も20人、25人、30人の3通り。
問題文に明記されていないのですが、この問題を解く上で最も重要な条件は
人数は整数
ということです。
Ａ＝Ｂ×1.2ですから、Ｂは5の倍数でないとＡは整数になりません。分数で考えれば、Ａ＝Ｂ×6/5ですからより気づきやすいことでしょう。
本問の「整数制限」など、当たり前なので明記されていない「隠れた制限」には様々なものがありますが、普段気づかなくても「ミス」で片付けてしまいがちです。問題では解答のための鍵になることが多いのできちんと整理してチェックリストを頭の中に作っておくことが大切です。
-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています～
1.
2.
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー