学習塾ロジム　今週の1問by 学習塾ロジム

１つの単純なゲームです。

　下の図のように、あるクラスの32人の生徒が並んでいます。
いま、前後左右の隣にいる人（斜めはなし）と手をつないで、全員で大きな輪をつくることにします。
ただし、全員２本とも手をつなぎ、同じところで３人以上が手をつなぐことはありません。
このとき、どのように手をつないだらよいですか。

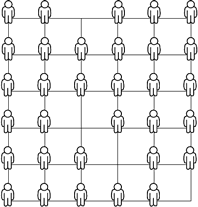
　誰と手をつなぐかが明らかな生徒に注目しましょう。

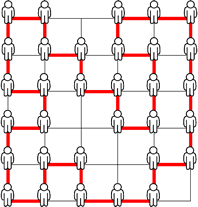
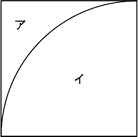
　簡単にするために、下の図のようにア～ミの32個の点を線で結ぶと考えます。
　ちなみに、与えられた条件から線が「交わる」「枝分かれする」「行き止まりになる」ということは避けなければなりません。このルールを守って、それぞれの点を隣り合う２点とうまく結んでいけばよいのです。

　まず、ア、イ、ウ、オ、ト、ノ、ヒ、フ、マ、ミの10点は、隣り合う点が２点しかないため、必然とつなぐ点がわかります（青）。

　続いて、これによってつなぐ点が決まる部分を探していきます（緑）。
　・カはキと結ぶことができないので、シと結ぶしかありません。
　・ヌはネと結ぶことができないので、ツと結ぶしかありません。
　・ヘはホと結ぶことができないので、ネと結ぶしかありません。

　続いて、これによってつなぐ点が決まる部分を探していきます（黄）。
　・テはネと結ぶことができないので、ス、ツと結ぶしかありません。

　続いて、これによってつなぐ点が決まる部分を探していきます（オレンジ）。
　・シはツと結ぶことができないので、スと結ぶしかありません。

　続いて、これによってつなぐ点が決まる部分を探していきます（ピンク）。
　・キはカ、スと結ぶことができないので、クと結ぶしかありません。

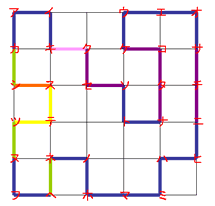
　ここまでくれば、あとは１つの輪になるようすが見えてくるはずです。それを結びます（紫）。
　・ク－セ－ソ、ケ－コ－タ－ナ、サ－チ－ニでできあがりです。

　ただいたずらに調べていくのではなく、このように「これしかありえない」という限られた条件部分を探すことは大切です。

-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています～

1.

2.
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー

　円周率は、3.14でしょうか？

　下の図のように、１辺が５cmの正方形の画用紙に、半径５cmの四分円（円を４等分したもの）を書き、アとイの部分に分けました。
この画用紙に、でたらめに100個の砂の粒（大きさはどれも同じ）をまいたところ、アの中には22個、イの中には78個ありました。また、四分円の線の上には砂の粒はありませんでした。
　これについて、次の問いに答えなさい。

(1) このことから、イの面積は何平方cmであるとわかりますか。

(2) このことからわかる円周率は、いくつですか。

　広いほど、砂はたくさん入ります。

(1) 19.5平方cm
(2) 3.12

　まず、でたらめに100個の砂の粒をまいているので、これらは均等に散らばっていると考えることができます。
つまり、２倍の広さがあれば２倍の個数の砂が入るということですから、面積と砂の個数が比例することがわかります。
　ここで、正方形の中の100個の砂の粒のうち、イの部分には78個入っているので、正方形の面積の78/100倍がイの面積になります。

　また、このときの円周率を□とすると、下の式から□＝3.12と求められます。

　さて、円周率はよく3.14が用いられますが、これは本当の値ではありません。
円周率は無限に続く小数で、計算で扱うのが不便であることから、
近似値（近い値）として3.14を使っているにすぎないのです。

例えば、入試問題を見ても「円周率を３で計算しなさい」や「円周率を3.1とする」などがあるのはそのためです。
よく注意しましょう。

-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています～

1.

2.
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー

　概算で見当をつける習慣はありますか？

　厚さが0.1㎜の紙を1回折ると厚さは0.2㎜、2回折ると厚さは0.4㎜になります。この紙は何回も折ることができるものとして、30回折ると厚さはどれくらいになりますか。次の中から最も近いものを選びなさい。
　　ア．1m
　　イ．10m
　　ウ．100m
　　エ．1km
　　オ．10km
　　カ．100km
　　キ．1000km
　　ク．10000km

　きまりにしたがって計算していくだけです。

カ．100km

一度折ることで、厚さは倍になります。これを繰り返すわけですから、単にどんどん2倍していけばよいのです。
　ここで、30回折るということは、「2倍」を30回続ければよいのです。

　しかし、ここで注意が必要です。「×2」が30個集まると「×60」にはなりません。どんどん2倍していくわけですから、2倍、4倍、8倍、16倍、32倍、64倍、128倍・・・というようになっていきます。これを30回繰り返すことで、答えにたどり着きます。

　ただ、これでは計算がかなり大変ですし、とんでもなく大きな数になることは容易に想像がつくでしょう。
この問題では、キリのよい選択肢から最も近いものを選ぶだけですから、大体の感覚がつかめればよいのです。
そこで、2を10回かけ合わせると1024になる（この知識を持っていなかったとしても、10回くらいまでなら簡単に調べられます）ことから、これをおよそ1000と考えて、以下のように計算できます。

-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています～

1.

2.
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー

　自分（ヒト）の体を理解していますか？

　下の図は、ヒトの体の骨を表しています。ヒトの体は、およそ200個の骨でできていますが、この中で最も長い骨はどれですか。次のア～オから選び、記号で答えなさい。

　ア．鎖骨（さこつ）
　イ．背骨（せぼね）
　ウ．骨盤（こつばん）
　エ．指節骨（しせつこつ）
　オ．大腿骨（だいたいこつ）

　ありません。

　オ．大腿骨（だいたいこつ）

　図から、最も長い骨を探すと多くの人がイ．背骨を選びます。
たしかに、首から腰までをつなぐ骨ですから「長い」イメージがあると思いますが、実はそうではありません。

　 背骨は、腰を曲げるために柔らかな動きができなければなりません（長い１本の骨だとしたら、曲げられません）。
よって背骨は小さな臼状の骨が軟骨によってつなげられる「軟骨接合」とよばれるつながり方をしています。
すなわち、背骨自体はとても小さいのです（下の図参照）。これより、ヒトの体の中で最も長い骨は、足のオ．大腿骨となります。

　さて、先週から小５の生徒たちがヒトの体について学習しています。この骨に関しては「３つのつながり方と動き」について主に学習するわけですが、それをただ暗記するだけではもったいありません。

１．ほう合・・・板状の骨がかみ合い、まったく動くことはないつながり方
２．なん骨接合・・・小さな骨が軟骨でつながっているため、しなやかに動くつながり方
３．関節・・・骨どうしが間をあけて筋肉やじん帯などで結ばれ、大きく動かせるつながり方

　これから、軟骨接合の背骨が小さな骨の集まりであることも、問題に活かしたいところです。

-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています～

1.

2.
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー

自分で導ける公式は、より記憶に残ります。

　次の図は、東京（北緯36°）における春分の日の地球と太陽の位置関係を表しています。この図の中に、この日の南中高度を書き入れ、求めなさい。ただし、必要な線などは消さずに残し、例のように、黒くぬりつぶして示すこと。

高度は、地面（地平線）からどれくらいの高さにあるかを表しています。

　高さを書き込む上で、まずは「地平線」を正しく書かなければなりません。地球は球体ですが、観測者の地球に対する小ささを考えれば平面と考えることができるので直線で表せます。また、太陽は地球から十分に遠いため、地球に届く光は太陽が放つ光の一部でしかありません。よって、平行光線であり、春分の日（秋分の日）はそれが赤道と平行になります。
　これより、90°－36°＝54°と計算できるのです。

　また、北緯をＮ°とすれば、この作図から「春分の日の太陽の南中高度＝90°－Ｎ°」という公式が導けたことになります。

-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています～

1.

2.
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー

選択肢がなければ答えが出せない問題もあります。

なめらかなカーテンレールと台でつくった装置を使って以下の実験を行いました。

＜実験１＞
　下の図のように、ななめの部分のカーテンレールを100cmとし、その上端からパチンコ玉を静かに転がしたところ、パチンコ玉はレールの右端から飛び出し、台から100cmの所に落ちた。

＜実験２＞
　角度は30°のまま、ななめの部分のレールの長さを２倍、３倍として、それぞれ上端からパチンコ玉を転がした。表１は、それぞれのパチンコ玉が飛んだ距離を表している。

＜実験３＞
　ななめの部分のレールの長さは100cmのまま、レールの角度を変えてそれぞれ50cmの高さの所からパチンコ玉を転がした。表２は、それぞれのパチンコ玉が飛んだ距離を表している。

＜実験４＞　
　 レールや台は実験１と同じ状態で、転がす玉の材質を変えた。ただし、それぞれの重さは異なっても、大きさは同じだった。表３は、それぞれのパチンコ玉が飛んだ距離を表している。

この実験結果から、ななめの部分のレールの長さは100cmのままレールの角度を変えて、それぞれの上端からパチンコ玉を転がすとそれぞれのパチンコ玉の飛んだ距離はどのようになりますか。次のア～クから選び、記号で答えなさい。

(1) レールの角度を45°にしたとき
(2) レールの角度を60°にしたとき

　　　　　　ア．71cm　イ．100cm　ウ．119cm　エ．132cm　

　　　　　　オ．141cm　カ．155cm　キ．173cm　ク．200cm

選択肢がなければ、解けません。

(1)ウ
(2)エ

　この実験より、球が飛ぶ距離は「はじめの球の高さ」によってのみ決まることがわかります。実験２から、はじめの高さが高いほうが飛ぶ距離が長いところまではわかりますが、比例関係にはなく、きまりまではつかめません。そこで、図にして比べてみると・・・

これから、(1)、(2)ともに、飛ぶ距離は100cm以上141cm以下であることが予想できます。また、当然(1)よりも(2)の方が飛ぶ距離は長くなるので、選択肢であてはまるのは119cm、132cmしかありません。

-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています～

1.

2.
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー

実験道具こそ、いろいろと工夫されているものです。

　ヒトは、呼吸をするときに体の中に空気を取り入れ、ある器官で必要な気体、不要な気体のやりとりをしたあとに、体から空気を出します。このように、体の中に取り入れる空気を吸気、体から出す空気を呼気とよぶことにします。これについて調べるために、太郎君は本でいろいろと調べながら下の図のようなそう置をつくりました。このそう置は、息を吸ったりはいたりするときにそれぞれゴム管のどちらか一方をおさえて使います。

問１　
太郎君が実験をしようとしたところ、先生が上の図のそう置にはまちがいが１つだけあることを教えてくれました。それを正す方法を、図の中の記号Ａ～Ｄを使って説明しなさい。

問２　
そう置のまちがいを正した後、このそう置を使って息を吸ったりはいたりすることをくり返していると、石灰水に変化が見られました。これについて、正しい結果を表しているものを次のア～オから選び、記号で答えなさい。

　　　ア．石灰水Ｘの方が石灰水Ｙよりもより白くにごった。
　　　イ．石灰水Ｙの方が石灰水Ｘよりもより白くにごった。
　　　ウ．石灰水Ｘ、Ｙともに同じように白くにごった。
　　　エ．石灰水Ｘが、石灰水Ｙの方へ流れ込んだ。
　　　オ．石灰水Ｙが、石灰水Ｘの方へ流れ込んだ。

呼気と吸気をそれぞれ通すための装置です。

(1) Ｄを石灰水Ｙから出す
(2) ア

(1) 呼気と吸気を通さなければならないので、装置の先を口にくわえて息を吐いたり吸ったりすることを考えてみます。

　・ゴム管の左をおさえて吐く・・・Ｄから呼気が石灰水に入っていきます。
　・ゴム管の右をおさえて吐く・・・Ａから呼気が石灰水に入っていきます。
　・ゴム管の左をおさえて吸う・・・Ｄから石灰水Ｙが口に入ってきてしまいます。
　・ゴム管の右をおさえて吸う・・・Ａから石灰水Ｘが口に入ってきてしまいます。

　つまり、これでは吸気を調べることができないため、ＡかＤを石灰水の外に出しておく必要があることがわかります。

１）Ａを石灰水から出した場合（吸気を石灰水Ｘに通す場合）
ゴム管の右をおさえて息を吸うことになりますが、石灰水Ｘに届く管がないためＢから取り入れた吸気（外気）が石灰水を通ることなく口に入ってしまい、実験になりません。

２）Ｄを石灰水から出した場合（吸気を石灰水Ｙに通す場合）
ゴム管の左をおさえて息を吸うと、吸気（外気）がＣから石灰水Ｙを通ります。また、ゴム管の右をおさえて息を吐くことで、Ａから呼気が石灰水Ｘを通ります。

(2) 呼気と吸気では、呼気の方が多くの二酸化炭素を含みます。よって、呼気が通る石灰水Ｘの方がより白くにごると考えられます。

-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています～

1.

2.
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー

データを読む訓練を怠ってはいけません。

ドライアイスは、二酸化炭素が固体になったもので、とても温度が低いものです。これによって水がこおることから、食塩水もこおるかどうかを調べるために、次のような実験を行いました。この実験について、次の(1)、(2)に答えなさい。

＜実験＞　小さなビーカーに、下の表のような12種類の食塩水を作り、これらの食塩水を、細かく砕いたドライアイスがたくさん入った水そうの中で冷やすと、どれも氷ができた。その後、これらのビーカーをある温度の冷凍庫に入れておいたところ、水10ｇに食塩2.0ｇをとかした食塩水の氷だけがとけた。ここで、表の中の温度は、食塩水がこおりはじめたときの温度を示している。

(1) 水30ｇに食塩1.5ｇをとかした食塩水は、何℃で氷ができはじめますか。

(2) 下線部で、この実験に用いた冷凍庫の中の温度として、
最も適当なものを次のア～オから選び、記号で答えなさい。

ア．０℃　　　イ．－５℃　　　ウ．－10℃　　　エ．－15℃　　　オ．－20℃

表のデータから、何が読み取れますか？

(1) －3.2℃
(2) ウ

　まず、食塩水は凍ります。これは、この実験結果を見ても明らかですが、
注意するべき点「は水と食塩の量によって凍り始める温度が変化する」ことです。

（本来、水が凍り始める温度は０℃ですが、何かが溶けている液体は凝固点降下という減少により０℃以下で凍り始めます）

　ここで、注意深く表を見てみると、次のことがわかります。

・一定の重さにおいて、食塩の重さと凍り始める温度が比例する

・一定の食塩水の重さにおいて、水の重さと凍り始める温度が反比例する

　つまり、一言で言えば水の重さと食塩の重さの比が一定であれば、
食塩水が凍り始める温度は変わらないということです。

(1) 水：食塩＝30：1.5＝20：１なので、表から－3.2℃とわかります。

(2) 下線部から、－12.8℃で凍り始めた実験の氷だけが溶けてしまっているので、冷凍庫の中の温度は－12.8℃より高いことがわかります。また、同様に表の－6.4℃で凍り始めた実験の氷は溶けていないわけですから、－6.4℃以下であることがわかります。よって、答えはウしかありません。

-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています～

1.

2.
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー

バネののびは、おもりの重さに比例します？

　下の図は、伸びたり縮んだりしていないときの長さが18㎝の特別な２本のバネＡ、Ｂを表しています。バネＡは両端を糸で結び８㎝以上伸びないようにし、バネＢは特殊な加工をして伸び方に工夫を与えたものです。

　また、下の左の表は、バネＡにいろいろな重さのおもりをつるしたときのバネの長さを表しています。また、右の図は、バネＢにいろいろな重さのおもりをつるしたときのバネの伸びを表したものです。これについて、次の問いに答えなさい。

問　下の図のように、重さのない棒にある重さのおもりをつるすことを考えます。棒が水平を保つように、このおもりを棒の真ん中につるすとき、おもりの重さは何ｇにすればよいですか。

テキストにおけるバネの常識にとらわれてはいけません。

500g

棒の中央につるすので、バネＡ、Ｂに加わる力は等しくなります。また、同様に棒が水平を保った状態で下がったので、バネＡ、Ｂの伸びがそれぞれ等しくなります。

　つまり、同じ力で同じ伸びになるので、完全にバネＡ、Ｂのグラフが一致する点とわかります。ここで、バネＡ、Ｂともに伸び方が特殊なので、バネＢのグラフにバネＡの伸び方を記入してみると、下の図のようになります。

　よって、図３よりそれぞれのバネの伸びは８㎝、それぞれのバネに加わる力は250ｇとなります。
したがっておもりの重さは250＋250＝500ｇとなります。

　さて、本来テキストで学習するバネの問題では「バネの伸びとおもりの重さは比例する」が常識となっています。

しかし、この問題のように特殊な加工をすることでそれに従わない場合もあるのです。「与えられた条件に従う」「問題作成者の誘導にのる」ことが物理単元ではよく見られます。

「解き方の暗記」にとらわれることなく、「何をすればよいのかを探る意識」を持ってほしいものです。

-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています～

1.

2.
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー

一問一答だけの学習は危険です。

　植物は、光を受けて「光合成」というはたらきを行う一方で、「呼吸」というはたらきを絶えず行っています。この「呼吸」について、次の（　　）にあてはまる言葉を答えなさい。

呼吸は、（　　）を得るためのはたらきです

「呼吸は光合成と逆のはたらき」とよく言われますが…。

生活エネルギー

　光合成は、葉緑体を持つ生物のみが行うことのできる特別なはたらきであり、このはたらきによって、生物が生きるのに必要な「光のエネルギー」を養分（でんぷん）の中に閉じ込めることのできます。そして、その養分をつくるための材料となるのが二酸化炭素と水であり、多くの参考書やテキストでは下の図のように表されています。

　一方、この光合成と逆のはたらきとして紹介されているのが呼吸ですが、落ちついて考えてみてください。光合成と逆のはたらきをするために呼吸があるのであれば、そもそも光合成、呼吸ともに行う意味がありません（せっかく光合成でつくった酸素と養分を、二酸化炭素と水にもどすのですから）。

つまり、二酸化炭素や水にもどすことは、呼吸の「目的」ではないのです。

　本来、呼吸は養分の中に閉じ込めた光のエネルギーを取り出すために行うのです。簡単に言えば、光のエネルギーというお金を養分（でんぷん）という名の貯金箱に蓄えるために行うのが光合成であり、その貯金箱をこわして中のエネルギーを取り出すために行うのが呼吸なのです。
　よって、呼吸を行う目的は「生活するためのエネルギー」を得るためというべきです。

-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています～

1.

2.
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー