実験問題は結果を予想しながら読み解く【対象学年:4年生以上】

昼間、明るく暖かいところで大きく開いていたチューリップの花が、夕方、うす暗く寒くなると、同じ花と思えないほど閉じていました。そこで、チューリップの花の開閉は光によるものか、温度によるものかを調べてみました。
チューリップの花の聞き方を図に示した角度で表し、この開いての角度を角度と呼ぶことにします。
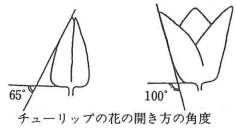
『実験1』 角度65度のチューリップの花を、温度20℃のままで十分に暗いところに3時間置きましたが、花の角度は変わりませんでした。その後、同じ温度のままで、明るくして3時間置きましたが、やはり、花の角度は変わりませんでした。
『実験2』 十分に明るい、温度20℃のところに置いた、角度100度のチューリップの花は、明るさを変えないで温度を7℃にすると閉じ始め、やがて角度65度になり、そのままの状態が続きました。
また、十分に明るい、温度7℃のところに置いた、角度65度のチューリップの花は、明るさを変えないで、温度を20℃にすると開き始め、やがて角度100度になり、そのままの状態が続きました。
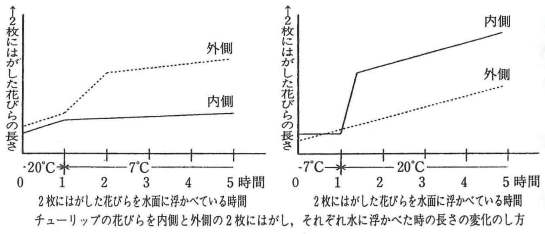
『実験3』 花の開閉のしくみをくわしく調べるために1枚の花びらを取り、その根もとから内側と外側の2枚にはがしました。この2枚にはがした花びらを水にうかべ、これを『実験2』のように温度を20℃~7℃へ、また、 7℃から20℃へ変化させ、2枚にはがした花びらの長さを測りました。その結果、長さの変化はグラフのようになりました。
以上3つの実験からチューリップの花の開閉について、次のような結論をだしました。
文の(1) -(10)に入る適当な語を下のア~スから選んで、記号で答えなさい。
チューリップの花が聞いたり閉じたりするのは、 ( 1 )に反応して開くのではないことが実験( 2 )から分かりました。( 1 )ではなく( 3 )の変化に反応して開くことが実験( 4 )で明らかになりました。花が開くのは( 5 )から( 6 )に移されたときであり、このような( 3 )の変化があったときに、花びらの成長が( 7 )のほうが( 8 )より大きいためです。このことは、実験( 9 )が示しています。したがって、 ( 3 )の変化によって開いたり閉じたりして、花びらは少しずつ(10 )なります。
ア.大きく イ.小き ウ.1 エ.2 オ.3 カ.温度 キ.光 ク.明るいところ ケ.暗いところ コ.高温のところ サ.低温のところ シ.外側 ス.内側
(桜蔭中)

・違いが二つ以上ある場合、ひとつの結果への原因が特定できません
・国語の問題だと思って文章を集中して読み込むこと

1.キ 2.ウ 3.カ 4.エ 5.サ 6.コ
7.ス 8.シ 9.オ 10.ア

一つの結果からその要因を特定する場合、唯一の違いに着目します。実験1では、明るさ以外は条件が固定されています。ここから明るさの違いが結果の違いを生んでいると判断します。
実験2は明るさが固定され、温度を変えることでチューリップが開花していることがわかります。
実験3では、温度を下げると(左側のグラフ)、外側が大きく成長し、また、温度を上げると(右側のグラフ)内側が成長することを読み取ります。従って、温度を20℃から7℃にした際は、花の外側が成長し、花は閉じます。
温度が上がろうが、下がろうが、花全体でみると成長しています。従って花は大きくなります。
----------------------------
実験結果から物事を考察する力を試す良い問題です。漫然と起きていることから穴埋めをするのでなく、それぞれの実験結果が何を表すのか考え続けた生徒とそうでない生徒に大きな差がついたのではないでしょうか。
こういった問題を解くコツは「結果を予想しながら問題文を読み解くこと」
考えてもみて下さい。普段の教室の実験でも「どうなるのだろうか」と考えながら参加するのと、なんとなくグループの中で言われたとおりに作業に参加するのでは、考察にたどりつくべく理解度が大きく変わります。試験でも擬似的に積極的に実験に参加する自分を意識してみて下さい。
「なにが起きているのか」集中力を切らさずに問題文・条件を読み込む姿勢が求められます。
読解力が要されるのは国語ではなくむしろこういった複雑な実験問題でしょう。
-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています~
1.
2.
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー





![]()