今週は雙葉中入試より1問です。

太郎さんはA町から一本杉を通って山頂Bまで登るのに1時間20分、山頂Bから一本杉を通ってA町まで下るのに55分かかります。ある時A町から山頂のB まで登るのに、一本杉と山頂のちょうど真ん中の地点で忘れ物に気が付きすぐ町までもどりました。そして忘れ物をとり、すぐ山頂へと向かい、はじめに町を出 発してから3時間5分後に山頂に着きました。もしも一本杉で忘れ物に気づいていたら、かかった時間はいくらだったでしょうか。太郎さんは登るときと下ると きはそれぞれ決まった速さで歩きます。
(雙葉中)

求めたい部分の距離の比を明らかにしてくれる ものは、時間の比しかなさそうです。

わすれものに気付いた地点をCとして考えます。
かかった時間より距離の比が求まる。
AB往復:80+55=135分
AC往復:185-80=105分
よって、AB:AC=105:135=7:9となる。
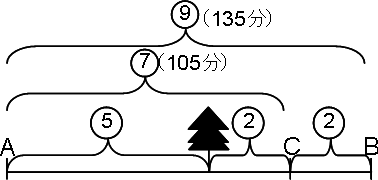
図のように距離の割合を考えると、
CBの割合は
9-7=2
となり、Aから一本杉までの割合は
9-2×2=5
となる。
よってA~一本杉間を往復するのにかかる時間は
105×5/7=75分
求めるべきは「A~一本杉間往復+A~Bの上り」なので
75+80=155分
答え 2時 間35分

速さと比の難問の典型例です。
雙葉中は処理能力だけでなく、かなり深く、丁寧な読み解きを要する問題を出してきましたが、女子校ではかなり重い部類の問題に入るでしょう。
ポイントは、
「求めたい片道の距離の比は、往復の距離の比と同じであり、往復にかかる時間の比から求められる」
という考え方です。
距離、速さの問題は、使う要素が「時間・速さ・距離」の3つしかありません。
この3つが、様々な形で見えにくくされていることが、この分野の難問の典型かつ唯一の方式です。
本問のように、片道の距離の比を求めたいけれども、片道の時間の比は求まらないなど、
求めたい値と同じ意味をもつ値を的確にさがさなくてはいけません。
ただ、よく考えてみると当たり前。
目の前の比の値に引きずられ、数学的に解こうとすると行き詰りますが、頭の中できちんと人が動いているイメージを作るとすぐに気付けます。
「同じ距離を歩いた時間の比」と聞くと、同じ方向に向かって、同じ時刻に並走していることを想像しがちですが、時期が違っても、逆向きに歩いていても良い のです。
「必要な情報」について、要点のみをしっかりと把握することで、視野が広がってきます。
~今回の問題から導かれる出題校からのメッセージ~
・数式と現実のイメージの結びつけを怠らないこと
算数の基本は、「数え上げ」と「測定」です。
つまり明確な対象がある場合がほとんどです。
「何を求めているのか。」「何を探しているのか。」に関して、
明確なイメージがなければ数えることも、測定することも不可能です。
にもかかわらず、勉強を進めていくと、とくにハイレベル勉強に進むにつれ、
数式のみを操作している時間が増えてきてしまいます。
常に、図式化することで数式だけでは表せない、
同値変形のヒントや言い換えのヒントを探るという、
算数を学ぶことの意味をきちんと教えてくれる良問です。