今週は浦和明の星女子中より1問です。

明子さんとお父さんは、それぞれA地点を出発して、8km離れたB地点まで行き、すぐに折り返してA地点まで戻ってくることにしました。お父さんは、明子 さんが出発してから何分か遅れて出発し、B地点の手前3kmの地点で明子さんを追い越しました。そして、B地点を折り返した後、B地点から1kmの地点で 明子さんとすれ違いました。明子さんは、お父さんがA地点に戻ってきてから110分後に、A地点に戻ってきました。ただし、明子さんとお父さんは、それぞ れ一定の速さで歩いたものとします。
(1)明子さんとお父さんの速さの比を、最も簡単な整数の比で表しなさい。
(2)明子さんの速さは分速何mですか。
(浦和明の星女子)

速さを求めるために必要な要素は決まっていま す。

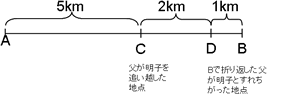
(1)上の図のC地点で、父が明子さんを追い越す。
ここを起点とすると、Dで二人が再会するまでに、
同じ時間で父は〔C~B〕+〔B~D〕=4km歩き、
明子さんは〔C~D〕=2km歩いたことになる。
よって、速さの比「明子さん:父」=2:4=1:2 答え 1:2
(2)(1)と同様に、C地点を起点に考えると、C地点を同時に出発したあと、
Bを折り返し地点としてAまでの11kmで110分の差がついたことになる。
二人の速さの比は、1:2なので、同じ距離を歩くのにかかる時間の比は2:1である。
この比の差である1が110分であったのだから、
明子さんがCからBを経由してAまでの11kmを歩くのにかかった時間は、110×2=220分である。
よって、明子さんの分速は 11000(m)÷220(分)=50m/分
答え 50m/分

速 さ=距離÷時間
速さの比は、「同じ距離」を移動するのにかかった時間の比
といった、当然の定義を見失わないことが大切です。
速さと比の問題は、様々な場所や、
出来事(折り返し、忘れ物による引き返し、途中で速度が変わるなど)によって、
問題文が長く、見た目が仰々しいものが多くなっています。
しかし、突破口は1つです。
速さ、距離、時間のうち、2つが揃う場面を探し出すことです。
本問でもC地点で父が明子さんに追いついてはじめて、
「2人が同時にスタートした」という条件がそろいます。
「どこから解いたらよいのか分からない」は、
「なにがわかれば答えがでるのか」という意識の欠如が大きな原因です。
速さの場合は基本は3つの要素です。
「必要な要素を洗い出して確認する」ことが基本です。
~今回の問題から導かれる出題校からのメッセージ~
・定義の深い理解が大切
速さを求めるのに一体何が必要なのか。
これは、難しいことではありません。
ただし、表面的な複雑さに目を奪われ、自分が今何を求めなくてはいけないのか、
についてしっかりとした方針が立てられないと、求値のための作業に集中できなくなります。
このレベルの問題は、「何を求めるのか」が決まったあとの計算も複雑なものになりがちです。
この複雑さによって、一行問題にかわり計算力を試しているともいえます。
つまり、正確に「これを求めれば答えにたどりつく」という方針をたてていないと、
長く複雑な計算の末に無意味な数値にたどり着いてしまうのです。
「何を求めるのか」は、数少ない選択肢を正確に確認しさえすれば
明らかになることが多いものです。
絶対に必要な要素の有無の確認は、定義についてしっかりと理解していることを
必要とするまさに質の高い基本問題といえる良問です。