「約数」の基本問題です。「割り算」において注意すべきポイントを確認しましょう。

656をある整数で割ると、いくらか余り、859を割ると余りが1減り、1198を割ると余りがさらに1減る。ある整数をすべて答えなさい。

実は「約数」の典型問題です。

問題文の「859を割ると余りが1減る」という条件は、「860を割ると余りが同じ」と言い換えることができます。
また、
「1198を割ると余りがさらに1減る」という条件は、「1200を割ると余りが同じ」と言い換えることができます。
つまり問題は656、860、1200を割って余りが同じになる整数を求めるということになります。
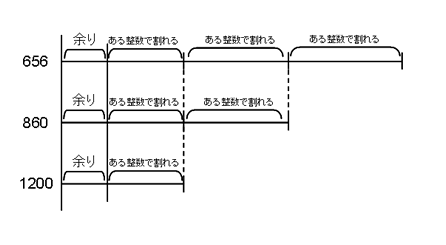
下の線分図のように考えると、それぞれの数の差である204と340が「ある整数」で割り切れることがわかります。
この2つの数の公約数は1、2、4、17、34、68です。
ここで656を割ったときの余りは2以上でなくてはならないことから、ある整数は3以上でなくてはいけないので、
答えは4、17、34、68の4つ。

「3つの整数を割った余りが同じ」というタイプの問題です。
出題されるときは、小問としてテキストに載っているものとほぼ同じ形です。
線分図で余りを左側によせてそろえる点が難しく、必ず一度は取組んでおかないと初見で解くのというのは非現実的なものです。
あまり変形の余地のない問題ですので、本問はかなり手が加えられている部類に入ります。
また割る数や余りを算出する問題では、「余りは割る数より小さい」という割り算の重要な制限を必ず意識しなくてはいけません。
そうすれば、本問のような複雑な問題文の中からでも、「余りは2以上」と「割る数は3以上」という条件を抽出することが出来るでしょう。