限界を考えることは、意外と難しいものです。

正方形の向かい合う辺の真ん中の点どうしを結ぶと、2つの合同な長方形に分割できます。

さらに、その長方形の長い方の辺の真ん中の点どうしを結ぶことで、右の図のように正方形を
作ることができます。そして、これを1回の「操作」と呼ぶことにします。
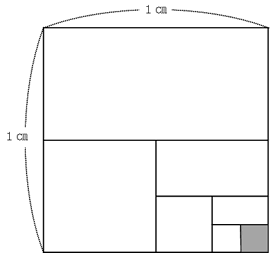
下の図は、1辺が1cmの正方形について、この操作を3回繰り返したものです。これについ
て次の問いに答えなさい。
問1
上の図で、3回までの操作を行ったときの最も小さな正方形(色つき部分)と、それ以外の部分の面積比を求めなさい。
問2
1を順に半分にしていくと、1/2 、1/4 、1/8 、1/16 、1/32 、1/64 、…となります。このような数のならびで、1番目を 1/2 とし、順に番号をつけていきます。つまり 1/64 は6番目となります。この数のならびで、100番目までの数の和と1はどちらが大きいですか。上の図を参考にして考え、大きい方を答えなさい。

図の各正方形の1辺に注目してみましょう。

問1 1:63
問2 1

問1
最も小さな正方形(色つき部分)ともとの大きな正方形は、相似比が1:8の正方形です。よって、面積比は1:64になるので、もとの正方形から最も小さな正方形(色つき部分)を除いた分は63になります。
問2
実際、100番目の数を求めようとするのは、かなり厳しいでしょう(10番目でさえも、 ですから)。
100個もたしていくわけですから、1くらい平気で超えそうですが…。
さて、ここで図をもとに考えてみましょう。もとの1辺1cmの方形の下の辺を「操作」によってで
きた正方形ごとに見てみましょう。すると、順に、1/2、1/4、1/8、1/16、1/32、1/64、・・・・ となりますが、
どれだけ操作を繰り返して分割していっても、絶対にもとの正方形の1辺を超えることはありません。
よって、たとえ何番目まで足したとしても、1の方が大きいのです(極限の考えは除きます)。
まとめ
「ひたすら足しまくるのだから、1くらい超えるだろう」という、常識(?)を覆す問題です。
高校数学でで極限を学べば、ある程度当たり前に感じることのできる内容ですが、小中学生には少々想像しがたいことでしょう。特に、問題のような図を与えず、ただ言葉や文章だけで出題したとすれば、おそらく全て(に限りなく近い数)の子供たちが1の方が小さいと答えるのではないでしょうか。
しかし、そんなイメージがわきにくいことも、図を用いてみるとあっけなく納得できるのです。図の力とは偉大ですね。
(どんなに1に近づこうとも、常にそのゴールまでの半分しか進めないというもどかしさがわかるはずです)
この問題を通して、不思議だと思い、少しでも算数や数学に興味をもってもらえたら嬉しい、そんな一問です。