情報に惑わされず、図形の本質を見抜くことが真の「力」です。

下の図は四分円OABの弧の上に点Cをとり、点CからOA、OBにそれぞれ平行な線を引き、長方形ODCEを作ったものです。このとき、辺DEの長さを求めなさい。ただし、∠OED=60度です。
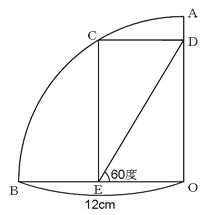

60度は、重要でしょうか?

12cm

辺DEは、長方形ODCEの対角線です。よって、DE=OCであり、辺OCは四分円の半径ですから答えは12cmとなります。
この解説のとおり、この問の答えを導くために「∠OED=60度」という情報は使いません。
受験テクニックを学んでいくと、どうしても与えられた情報(特に頻出のテクニックや知識に関わる情報)から答えを探っていくことが多いもので、もちろんそれが重要であることが多いのですが、逆にその情報に惑わされて本来の解答を導くポイントを見失う危険性があるのです。
この問題であれば、「DEが長方形の対角線である」ということ以上に、「∠OED=60度」が頭から離れず、OE:DE=1:2だから・・・などと考え始めた人が多いのではないでしょうか。そのような人は、この問題が「BEの長さを求めなさい」の方が意外と即答できたかもしれませんね。
ちなみに、BE=OB-OE=OB-DE÷2=6cmです。
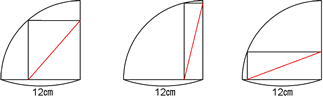
余談ですが、60度にこだわらず下の図のようにどのような長方形を描いたとしてもDE=12cmということですね。
--------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています~
1.
2.![]()
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー