シャドーの威力を感じてください。
学校から800ｍはなれたところに図書館があります。太郎君は分速100ｍ、次郎君は分速80ｍで学校から図書館へ、花子さんは分速70ｍで図書館から学校へ同時に出発します。花子さんが太郎君と次郎君のちょうど真ん中にくるのは、出発してから何分後ですか。
ありません。
５分後
まず、３人とも同じ時間動いていることから、
条件を満たすまでに動いた道のりの比は、太郎：次郎：花子＝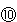
：
：
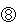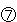となります。
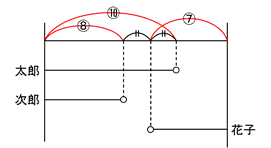
ここで、下の図のように動きを表してみると、
学校と図書館との間の道のりは（ －）÷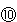
＋＋＝
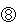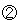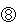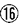と表せます。
これが800ｍであることから、太郎君の進んだ道のりは800×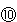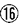（／）＝500ｍとわかります。
よって、求める時間は500÷100＝５分となります。
さて、ここでちょっと違った見方でこの問題を解いてみます。
花子さんは、太郎君と次郎君の真ん中まで行くことになるので、「常に太郎君と次郎君の真ん中を進む、架空のミスターＸ」がいると考えれば、ただのＸと花子さんの出会いの問題になります。
このとき、Ｘの速さは太郎君と次郎君のちょうど平均になるので、分速90ｍとなります。よって、800÷（90＋70）＝５分後と求められます。
このように、条件を満たすための特別な動きをする架空のもの（者、物）は、受験界で「シャドー」と呼ばれ、特に速さの問題で威力を発揮します。
時計算、動点問題、仕事算など、速さに関わる問題で応用がきくので、ぜひいろいろと試してみてください。
-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています～
1.
2.
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー