「ニュートン算=倍数算+仕事算」と、気づいていますか?

ある牧草地で、牛10頭を放しておくと10日で草を食べつくしてしまいます。また、この牧草地で、牛12頭を放しておくと8日で草を食べつくしてしまいます。
では、この牧草地で、牛18頭を放しておくと草をたべつくすのに何日かかりますか。
ただし、この牧草地は一定の割合で草が生え続けています。

増加と減少が同時に起こる、いわゆるニュートン算です。

5日

さて、ニュートン算が難しいと感じられる点はどこでしょうか・・・?
それは、「増加と減少が同時に起きている」という点に加え「増加と減少のうち一方は個数に比例するものの、他方は個数に関係なく絶えず一定である」という点に他なりません。
その点を単純化してある問題が、いわゆる仕事算です。
「12人ですると6日で終わる仕事を8人ですると何日か?」
実際に行う仕事は人数に比例しますから、1人で1日にする仕事の量を1とすれば、全体の仕事量は12×6=72となり、これを8人で行うので72÷8=9日とわかります。

しかし、ここで絶えずこの仕事が1日に増えていくことを考えます。
例えば、仕事を行う人数に関係なく、毎日仕事が2ずつ増えていくとしましょう。
すると、12人では1日に12の仕事を行いますが、2だけ増えてしまうので結果として12-2=10しか仕事をすることができません。
また、8人の場合も同様に1日あたり8-2=6しか仕事をすることができなくなってしまうのです。
これにより、実際に12人で行う仕事の量は(12-2)×6=60となり、これを8人で行うとすれば60÷(8-2)=10日となるのです。
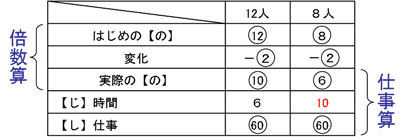
このように、一見複雑そうなニュートン算ですが、仕事算のように表に整理してみると簡単です。上3段が能力(仕事の速さ)の変化についての倍数算、そして下3段が実際の能力での仕事算となっているのです。
では、ニュートン算の仕組みがわかったところで、本題を解いてみましょう。
まず、表に整理すると下のようになります。
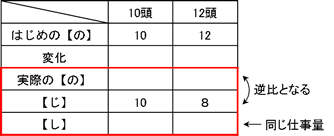
同じ仕事(草を食べること)をするのに、10日と8日かかっているわけですから、実際の【の】はその逆比となり4:5であることがわかります。これにより、はじめに10:12だった能力が、同じ分だけ減って4:5になっているので、一定である差で比をそろえます。これにより、牛1頭あたりの能力が1で、変化が-2であることがわかります。
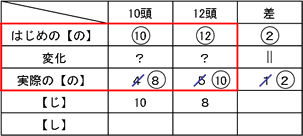
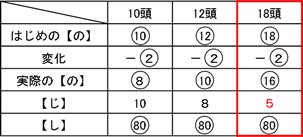
全体の仕事が8×10=80とわかるので、同じようにして牛18頭の場合を考えてみます。実際の能力は18-2=16となり、80÷16=5日と求められます。
-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています~
1.
2.![]()
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー