今週は灘中入試より1問です。 2006-02-06
今週は灘中入試より1問です。

下の図 で、ACの長さは10cm、AFの長さは6cmです。
(辺ADの長さ):(辺BDの長さ)=3 : 2
(辺BEの長さ):(辺ECの長さ)=5 : 2
とするとき、図の角(ア)の大きさを求めなさい。
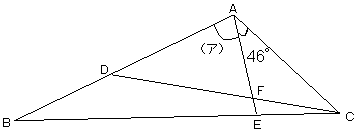
(灘中)

「角アを求める」はどこから手をつけていいのかわかりませんよね。まず、手持ちの選択肢を冷静に洗い出して みましょう。

下の図のように辺ABと辺CGが平行となるように、AEの延長戦上に点Gをとり、辺EGと辺GCという補助 線を引く。
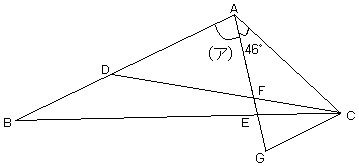
すると三角形ABEと三角形ECGが相似 (相似比はBE:ECより5:2) となる。
また三角形ADFと三角形GFCも相似となる。
AD:DB=3:2なので、AD:DB:GC=3:2:2となる。
よって、三角形ADFと三角形GFCの相似比はAD:GC=3:2となる。
以上よりAGの長さは
6× (3+2)/3 =10cm
となる。
ここでAC=10cmと問題文にあるので、三角形AGCはAC=AG=10cmの二等辺三角形となる。
錯角を利用し、角(ア)=角G。
よって角(ア)=角G=(186-46)÷2=67度
答え 67 度

解くための第一歩。それは
「そもそもこの角アなんてどうやっ たら求まるのか?」
としっかり立ち止まって、方針を考えるこ とです。
図形のなかのある角度の大きさが判明するときに必要な要素が
どのようなものなのかを精査してみることが大切です。
三角定規と同じ形の三角形や、正三角形、角度がわかっている二等辺三角形などはここには1つもありません。また3つの内角のうち 2つがわかっているような三角形も1つもありません。
ここまでしっかりと整理、チェックを進めて行くと
「どこかに 合同、相似の図形を見つければ、角アが判明するのではないか 。」
という突破口となる方針にたどり着きます。
~今回の問題から導かれる出題校からのメッセージ~
・出来ること、出来ないことをしっかりと見極める力が大切
本問は、1日目の問題です。
つまり1問あたり3分~5分で解き 進めなくてはいけない問題群の中の1問です。
何も考えずに、辺の比から面積比を求めたりし始めると泥沼です。
そもそも面積比から角度を求めることはとても難しいですし、
そのような問題に出会ったこともないはずです。
「とりあえず~」という浅い考えで動き始めると5分はあっという間です。
情報を精査して方針を決定するというレベルの高い判断力が求められています。
対策は、角 度の練習問題を数多くこなして行く中で、
解法を自分の中でしっかりと整理しておくことです。
そして、問題文を読んだ時に、
自分の考える解法を進める上で 十分な情報があるのか、足りない情報は何か、そしてその足りない情報はどこからか導き出せるのか
という思考回路が動き出すような日頃のトレーニングが大切です。
そうすれば、そもそも情報が足りずに行き詰まることになる解法にはまり込む危険性を回避できるのです。
一つ一つからしっかりと学んで行く問題演習が大切。
こなすこ とが目的になってきた受験生の勉強姿勢に警笛をならす良問です。