学習塾ロジム　今週の1問by 学習塾ロジム

公式は、理解してこそものになります。

　図１のような幅２cmの長いテープをさまざまな角度で多くの部分に切り分け、長さの同じ切り口どうしをつないでいきます（のりしろは考えません）。つなぐときの内側の角はすすべて180°より小さくなるようにします。これをつないでいったところ、図２のように１周してちょうどつながりました。この図形の外周の長さは117cm、内周の長さは99cmです。

　

　　　　　　　
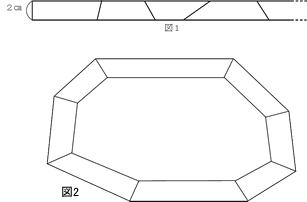
問１　図２の図形の面積を求めなさい。

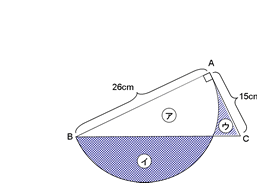
問２　図２の図形を、下の図３のように外周と内周ちょうど真ん中のところで２つに切り分けました。このとき、外側の部分と内側の部分（色つき部分）の面積の比を求めなさい。

そもそも、このテープの長さは何cmでしょう？

問１　216cm2
問２　25：23

問１　
テープを切り分けたそれぞれの台形の上底と下底に注目します。
図２のつなぎ方では、これらのうちすべて短い方をつないで内周、すべて長い方をつないで外周が作られています。
つまり、すべての台形の上底と下底の合計（下の図でのア＋イ）は、外周と内周の和の117cm＋99cm＝216cmとわかります。

よって、このテープの長さは、216cm÷２＝108cmです。
図２の図形の面積は、テープ全体の面積なので、答えは２cm×108cm＝216cm2となります。

問２　
外周と内周ちょうど真ん中のところで２つに切り分けた線は、テープを半分に切り分けた線になるので、その長さは108cmです。

ここで、図３の外側の部分、内側の部分ともに高さ１cmの台形の和と考えることができます。
まず、内側の部分は、
上底の和が99cm（図２の内周）、
下底の和が108cm（テープを切り分けた線）とわかります。

同様に、外側の部分は、
上底の和が108cm（テープを切り分けた線）、
下底の和が117cm（図２の外周）とわかります。

すべて高さの等しい台形ですから、面積の比は上底と下底の和で求められます。
これより、外側の部分：内側の部分＝（99＋108）：（108＋117）＝25：23になります。

まとめ 　問１について、最終的に面積を求めた式を思い返してみてください（２cm×108cm＝216cm2）。
何か気付く ことがあるでしょうか？　

２cmはテープの幅、108cmはテープの長さでありちょうど真ん中で切り分けた線の 長さでもあります。
つまり、図２の図形の面積は、図形のちょうど真ん中の長さ（センターライン）に
テープの幅をかけて求められているのです。
（幅２cmのローラーで、108cmまっすぐ引けば、塗られた面積はもちろん 216cm2になりますね）

この公式は、中学入試の世界でセンターラインの公式とよばれ、
主に図形の転がり移 動の問題などで重宝されているものです。

しかし、このような公式もむやみやたらに使っていては、本来使るはずのない状況で使ってしまう危険性もあります。
どのような場合に、どのような部分を求めるために使う公式なのかを、日頃から意識していろいろな公式とつきあっていってほしいところです。

ストッパーには、良問がそろっています（平成16年度　女子学院中学校より）。

下の図で、長方形ＡＢＣＤの辺ＡＢの長さは４cm、辺ＢＣの長さは８cmです。
このとき、対角線ＡＣを１辺とし、点Ｄを通る長方形ＡＣＥＦの面積を求めなさい。

長方形ＡＢＣＤと長方形ＡＣＥＦ、どちらが大きく見えますか？
また、ルート記号は不要です（大ヒントかな？）。

32（平方cm）

ＡＣが長方形ＡＢＣＤの対角線であることから、三角形ＡＣＤ＝４×８÷２＝16（平方cm）とわかります。
ここで、三角形ＡＣＤは長方形ＡＣＥＦの半分であることがわかります。

（長方形ＡＣＥＦ＝ＡＣ×ＡＦ、三角形ＡＣＤ＝底辺ＡＣ×高さＡＦ÷２より）
よって、長方形ＡＣＥＦ＝16（平方cm）×２＝32（平方cm）となります。

解説を見てわかるとおり、なんてことない問題です。

しかし、時間が限られた（しかも入試本番で最高に緊張している）時間で処理しなければならないとしたら…？

まず、ＡＣの長さを求めようとして…、ＡＦの長さに注目して…となってしまうことでしょう。

入試問題には、このように一見簡単に見えるにもかかわらず、即答できず、思考を停止させる「ストッパー」が数多く存在します。
これこそまさに、良問の類といえるでしょう。

　さて、この問題を、見た目と同様に容易に処理するには、次の２点が必要です。
1）与えられた情報（辺の長さ）から、わかることは何か？
2）図形分割における、面積比の基本（←問題演習で身につけられます）

　仮に、この問題が即答できないとしても、長方形ＡＢＣＤと長方形ＡＣＥＦはどちらが大きいか？
くらい、意識して欲しいところです。

（問題）
AB=3cm 、BC=4cm、CA＝5cm、の直角三角形ABCの斜辺CA上に点Pをとったところ、2つの三角形ABPと三角形PBCの周の長さが等しくなった。このとき三角形ABPの面積を求めよ。

（解説）
「構成要素は違うが合計が同じ」という条件が与えられているところから、和と差について考える問題であると気付けることが突破口です。

最近の上位校での流行なので対策は進んでいますが、問題文を吟味して条件の本質的な意味を考えるという点ではやはり難問です。

求積問題では、「明らかに通常の解き方では求めることができない。」という判断をすることが比較的容易ですので、その場合に考えられる手法について確認しておくと良いでしょう。

最近は～算について学ぶ基本例題とは見た目が全く違う問題を出そうという姿勢が各校で見られます。

数学の先生たちの腕の見せ所といったところですが、受験生にとっては～算の仕組みについてしっかりと理解しておく必要性が高まってきていることになります。

有名な公式の仕組みを思い出しましょう

半径2cm、弧の長さ10cmのおうぎ形の面積を求めなさい。


ノーヒントでいきましょう。

おうぎ形の面積は「半径×弧の長さ÷2」で求まるので求める面積は

2×10÷2＝5平方センチメートル

おうぎ形の面積を「半径×弧÷2」で求めるという公式はあまりテキストでは扱われません。

ここで、円の面積の公式についての教科書の説明を思い出してみましょう。

円を細かくケーキ状に切り分けて、並び替えて長方形として考えるというものです。

この説明では長方形のたての長さは円の半径と同じ、
そして、よこの長さは円の円周の長さの半分となります。

この考え方に従うとおうぎ形についても、同様にケーキ状に切り分け、並び替えて長方形として計算することができます。
この場合もたての長さは円の半径となり、よこの長さは弧の長さの半分となるのです。

公式の仕組みは、学校の教科書などでは丁寧に説明されているのですが、
普段の受験勉強ではその運用にばかり目がいってしまいがちです。

様々な公式が作られる仕組みに注目し、しっかりと理解しようという姿勢は、
上位校において数学の勉強を進める上では必須のものですので、目先のテストに気を取られすぎずしっかりと取組みましょう。

東邦大東邦中。今年度入試から速報第一弾。公式の構造を見抜く力が問われます。

下の図のように直角三角形ＡＢＣとＣＤＥが頂点Ｂ、Ｃ、Ｄが同一直線上になるように並んでいます。このとき、三角形ＢＣＥの面積を求めなさい。

(東邦大東邦中）

底辺と高さがそれぞれわからなくても面積は求めることができます。

求める三角形ＢＣＥの底辺を辺ＢＣと考えると高さは辺ＥＤとすることができる。
よって、求める面積は辺ＢＣ×辺ＥＤ÷２で求めることができる。

ここで三角形ＡＢＣとＥＤＣが相似であることに着目する。すると
辺ＡＢ：辺ＢＣ＝辺ＥＤ：辺ＤＣが成り立つ。
つまり
７：辺ＢＣ＝辺ＥＤ：４
ゆえに
７×４＝辺ＢＣ×辺ＥＤ＝２８

求める三角形の面積は
辺ＢＣ×辺ＥＤ÷２なので
２８÷２＝１４

答え：１４平方センチメートル

円に内接する正方形の面積を与えて円の面積を求めさせる問題
（半径はわからないが、半径×半径の値はわかるというタイプ）の類題です。

本問も、同様に明らかにわからないであろう底辺と高さを個別にとらえずに、
まとめて考えてみるという視点が大切です。

これは、どの教科書、参考書にものっている円の問題に取り組んだ後に、
一般化された解法として習得しておかなければ対応できない問題です。

～今 回の問題から導かれる出題校からのメッセージ～
公式の構成要素の意味を吟味することが大切

本問で取り扱ったもの以外にも一般的に知られている公式の中で、
いくつかの項目をまとめて考えると見通しが立つというものがいくつか存在します。

例えば、扇形の面積を「半径×弧÷２」と変形できたり、
半径/母線で円錐の中心角を求めることができるものもその例です。

無味乾燥な数式も見方を変えると図形的な意味をとらえることができることがよくあります。

面積図はその代表例です。
面積図というと、小学生用の受験のテクニックのように思われがちですが、
数式の図形的性質に着目して解くというのは中学生以降では常套手段です。

遠回りだとか、本質的でないといって避けることなく、
数式に含まれているそれらの性質を楽しむ姿勢が大切です。
本問はその姿勢が問われる良問です。

麻布中より。簡単な図形の面積の公式を何パターンも思いつけますか。

下の図のように1辺10cmの正方形の内側で接している円と、その円周上に頂点がある正方形があります。内側の正方形の面積を求めなさい。

(麻布中）

正方形・円の面積はどのようにしてもとまるのだったでしょうか。

ポイントは、正方形の面積は「対角線×対角線÷２」でも求めることができることです。

内側の正方形の1辺は、求めることができません。

しかし対角線は、円の直径と同じであることがわかります。

そしてこの円の直径は、外側の正方形の1辺と同じ長さ、つまり10cmです。

内側の正方形の対角線が10cmであることから求める面積は
10cm×10cm÷2＝50平方センチメートル

答え：50 平方センチメートル

ここ数年、中堅・上位校の一行問題で流行の問題です。

円の面積を習い終わった４，５年生の時点でじっくり考えさせたい問題です。

円周率3.14の意味や、半径×半径の値との関係など、
円の面積を求める公式の要素一つ一つをしっかりと考えておくことでしか対応できません。

例えば、円の面積の公式の成立過程を理解していると、
半径と弧の長さだけでおうぎ形の面積を求めることができます。

このように、求積の公式の要素が、習ったとおりに素直に与えられていない問題は、
式の数学的な意味やほかの図形との関係性の理解力が問われます。

その週のテストに追われるように公式を覚えて済ましてしまっていると、
入試本番で痛い目にあいます。もう一度確認する機会にしてみてください。

～今回の問題から導かれる出題校からのメッセージ～
数式の意味を様々な角度から見る能力が大切

たとえば円の面積を求める公式：半径×半径×3.14を覚えたとします。

それでは、ある円が与えられたときに半径の長さがわからなければ
円の面積は求められないのでしょうか。

実は、半径は不明でも、「半径×半径」の値は求めることが出来る場合が数多くあります。

上記の公式の変数の部分を過不足なく把握しておくことで、
必要な条件を必要な形で探し当てることができます。

面積などの公式、そしてその公式の成立過程をしっかりと見直すことで
「どの値がわかれば算出できるのか。」という視野を広げておくことが大切です。

既存の知識として与えられたものを鵜呑みにせず
分解して確かめる姿勢は、
まさに麻布中の求める科学的な検証能力と同じものだということが出来るでしょう。

今週はフェリス女学院中より1問です。

下の図のように、直角三角形ABCと半円があります。
部分と部分の面積の合計は136．97cmです。
部分の面積を求めなさい。　（フェリス女学院中）

まさに分野融合問題です。

問題 の図を下のようにア～ウの3つの部分に分けて考える。

問題文の条件より、イ＋ウ＝136.97である。・・・（１）

ここで、イ、ウにそれぞれアを加えて、半円、直角三角形として考える。
ア＋イの半円の面積は13×13×3.14÷2＝265.33
ア＋ウの直角三角形の面積は15×26÷2＝195
この2つの値の差は、そのままイとウの差として考えることが出来る。

よって
イーウ＝70.33・・・（２）

（１）と（２）より
和差算によってイ、ウを算出できる。
イ＝（136.97＋70.33）÷2＝103.65

答え 103.65cm

04: 解説
前 回の灘中の問題の最後の山場を乗り越えるための練習問題です。
面積における、和差算は単純なものであっても、相当の問題文読解力が求められます。
「和」という条件から、「差を探す」という流れが身についているかどうか。
問題形式が図形であっても、割合であっても、速さであっても同様です。

～今回の問題から導かれる出題校からのメッセージ～
・所与の条件を丁寧に類型化する力が大切
前回の灘中の問題と同様、表面的な題材の形式とそこで使われる技術は、
塾の一般的なカリキュラムほど単純なものではありません。
図形の和差算、速さの消去算など、数多くの融合問題が存在します。

速さは・・・、流水算は・・・という単純なパターン解法の暗記では対応できません。
必要なのは、
問題分によって与えら れる条件が、どの方針に誘導しているのかを見抜く力です。

「分からない数と与えられた状況の数が同じならば消去算」
「和を与えられる場合は、差を見つければ和差算で答えが出る」
など、解法の本質をつかんでおくことが重要です。

途方もない作業のように思えますが、無駄な何百もの問題演習よりも時間もかからず、
頭を使って普段の勉強をまとめるクセがつきますので、是非取り入れてもらいたいものです。

フェリスをはじめとして、このレベルの勉強が要求される入試問題を出題する学校は限られています。
しかし、出題されないからといって、考えない勉強法が身についてしまうと、
想像以上に入学以降の勉強に手間取ることになるのです。

学校の指導方針と強い信念が読み取れる良問です。

今週は灘より1問です。

下の図で、ABとCDは垂直になっています。AE＝24cm、 BE＝6cm、CE＝18cm、DE＝8cmになっています。円の面積は785cm となっているとすると、斜線部分の面積の和を求めなさい。

公式で求めようのない図形の面積を測定するには、いくつかの方針しかありません。

下の 図のように、CDに平行な補助線KLとABに平行なHGを、AB、CDと対称となるように引きます。
（交点にはそれぞれ記号をふります。）
問題の円を下のようにア～ケの9の部分に分けて考える。
斜線部＝ア＋イ＋カ＋ケ
残り＝キ＋ク＋エ＋ウ＋オ
である。
斜線部と残りのそれぞれを構成する部分を比較すると
ア＝キ、イ＝ク、カ＝エ、ケ＝ウであるので、オの部分の面積がそのまま両者の差となる。
オの面積はIE×EF＝18×10＝180となるので、
和差算を使い、（785－180）÷2＝302.5cm

答え　 302.5cm

図形は単純ですが、いくつもの思考の山場がある難問です。
まず、本問のようないびつな図形の面積は、そのまま求めることはできません。

1）等積・相似の基本図形を見つける。
2）基本図形に分解する。
がオーソドックスな方針です。

2）で補助線による分解が本問の方針となります。
基本図形とは、
「正三角形や正方形、おうぎ形、等脚台形などの求積が容易なもの」、
「問題の図形と合同、相似なもの」
「対称性のある形」
の3パターンと考えてよいでしょう。

本問では、「対称性のある形」に分解してみます。
この分解という作業に短時間で論理的に
（つまり上述の基本的な選択肢の外に無駄に陥ることなく）たどり着くことが、
本問において測定されている能力といっても過言ではないでしょう。

解答のような、和差算タイプの求積問題は、一度は取組む基本問題です。
（これまで出会ったことのない人は、今回がその機会でしょう。）
そこにたどり着くまでの条件を整えさせるという難問です。

～今回の問題から導かれる出題校からのメッセージ～
・思考の類型化が大切
算数のカリキュラムは、題材によって分けられています。
例えば、速さ、面積、割合・・・・。
しかし、本問はそのような題材ごとのパターン演習のみで作り上げられた算数の力を
簡単に切り捨てる問題です。

中学受験算数の題材がどのようなものかは、
テキストの目次や過去問の分析表によって明らかになっています。
しかし、どのような頭 の使い方が要求されているのかに着目して勉強し、
内容を整理している生 徒はほとんどいません。
この問題を単なる求積問題の一つとして片付けているようでは、いくら量をこなしても、
このレベルの問題の要求に答えることはできません。
あるトップクラスの生徒は、本問について「ベン図の考え方と似ているかな？」と
ノートに書き記していました。自分の頭で、思考の類型化を試みている確かな証拠です。

「総合問題」とは、見たことのない題材に、基本的な思考方法を当てはめる問題です。
その「基本的な思考方法」をきちんと整理することを怠っていると、
教科書の範囲名の書いていないテストが始まる時期、全く手も足もでなくなります。
出来る子は、自然と頭の中でやっていて、出来ない子はやっていない。
そして普通 のカリキュラムは、これを要求する形では並んでいないのが現状なのです。

この差を地頭の差といって、諦めるのではなく、勉強の中つねに
「これはあの問題と頭の使い方が似ている。」といったフォローをしてあげることが指導者、
保護者として大切な作業です。

今週は函館・ラサール中より1問です。

AB=1cm、BC＝1.5cmの三角形ABCにおいて、角 BACの大きさは、角ACBの大きさの2倍です。
この三角形ABCをADを折り目として折るとBとEが重なります。
次の問いに答えなさい。
（１）CDの長さは何cmですか。
（２）ACの長さは何cmですか。
（３）角DECの大きさは角ACBの大きさの何倍ですか。
(函館ラ・サール）

相似の問題です。

「こ の三角形ABCをADを折り目として折るとBとEが重なった」という問題文の設定より、
三角形ADEと三角形ADBは合同なので、角EAB＝角DABとなる。

これと「角CABは角ACBの2倍である」という条件を合わせて考えると、
角ACB＝角EAD＝角BADとなる。この角の大きさを下の図に「○」で表すこととする。（図1）

ここで、角ADBは、三角形ADCの外角であることから、角ADB＝角CAD+角ACDとなり、
○×2の大きさとなる。
また、折り返したという設定より、角EDAも同じく○×2の大きさとなる。（図2）

さらに、角EDBは、三角形CEDの外角であることから、角EDB＝角CED+角ACBとなる。
角EDB＝○×4、角ACB＝○×1であるので、角CED＝○×3となる。（図3）

（１）三角形ABCと三角形DBAは、2つの内角が等しいので相似である。
三角形ABCにおいて、AB：BC＝1：1.5であるので、三角形DBAにおいてもDB：BA＝1：1.5である。
BA＝1cmであるから、DB＝1×2/3=2/3cmとなる。
よって、CD＝1.5－2/3＝5/6cmとなる。
（答え）5/6cm

（２）下の図より、三角形ADCはCD＝DAの二等辺三角形である。
よって、（１）よりCD＝DA＝5/6cmとなる。
DA＝5/6を、三角形ABCと三角形DBAの相似の中に当てはめると、
AC＝DA×3/2=5/6×3/2=5/4=1.25 cmとなる。
（答え）1.25cm

（３）下の図より、
（答え）3倍

本問は、解答の下線部である、

「2つの内角が等しいから」相似

という知識を使いこなせるレベルで定着させているかどうかがすべてを握っています。

中学入試ではあまりみかけないタイプの相似で す。
これは、
「2つの三角形が相似となる3つの条件」
をしっかりと頭に入れていなければ気付くことができません。

多くの生徒は、俗に言うピラミッド型と砂時計型の相似にしか気付けません。

そして、「なぜ相似といえるか？」という問い に正確に答えられる生徒も少ないのが現状です。

「相似ならば～」についての練習は数多くこな しているのですが、「～だから相似」については全く見逃されているのが現状です。

合同とあわせて、成立 条件をきちんと整理して、
合同・相似の発見、証明に取組んでおかなければ、
本問のような相似を見つけることは絶対に不可能でしょう。

「雑多な情報の中から、既存のフレームと比較し、適応可能なものを探し出す。

というものがあります。

そもそも「自分が解けるものとは、どのようなものなのか」がわかっていない生徒が、
「自分が解けるもの」を見つけられるはずがありません。

このタイプの問題は、解説を読めば必ず「あ、そうか。」と理解したかのような感覚に陥りがちですが、
問題は「その場で気付けなかった」という事実です。

「なぜ気付けなかったのか。」

それは、往々にして「いま探すべきものについての定義が明確にはわかっていない。」ことが原因なのです。

今週は慶應中等部より1問です。

下の図のように、1辺が15cmの正方形ABCDとおうぎ形ABDがあります。点Eは、辺AB上にあり、色のついた2つの部分の面積は等しくなっています。このとき、AEの長さを求めなさい。
円周率は3.14とします。

　（慶應中等部） 　

「明らかに測定不可能な面積の差について 考える問題」といえば。。。

下の 図のように3つの部分を（ア）、（イ）、（ウ）とおきます。

（ア）＝（イ）なので、それぞれに（ウ）をたして、
（ア）＋（ウ）＝（イ）＋（ウ）も成立します。
（ア）＋（ウ）の面積は、半径15cmの円の4分の1なので
15×15×3.14÷4＝176.625
となり、これが（イ）＋（ウ）である台形AECDの面積となる。
よって
（AE＋15）×15÷2＝176.625
という式が成立し、これをとくと
AE＝8.55cmとなる。

答え　8． 55cm

平面図形内での、面積の差、和についての問題 です。

しっかりとした基礎演習をもとに、

「二つのぬられた面積の測定は無理である。」
「三角形EBCの辺EBを導き出すのは無理である。」

という決断をできる かどうかが大切です。

また、和の問題、差の問題では実数が求まることはほとんどありません。
この点に着目すると、方針の選択肢はせばまり ます。

同様の問題（正方形の中に直角三角形が向かい 合って入っているもの）
に4年生で出会っているはずです。
その問題をきちんと抽象化しておけるかどうか が分かれ目でした。

～今回の問題から導かれる出題校からのメッセージ～
・基本問題の整理能力を鍛えよう

基本問題を応用力を持たせるかたちで整理できているかどうかが問われています。

首都圏上位校の中では、 女子学院とならんで算数が基本問題の高い処理能力をもとめる形式となっている慶應中等部ですが、単純な繰り返しだけでは、対応できません。

基本問題＝簡単な問題ではありません。

その先に、多様な応用問題が考えられる土台となる考え方が含まれている問題が
ここで問われる”基 本問題”なのです。

なぜ、基本問題といわれるのか。
その裏に隠されたとても大切な考え方は何か。
そして他分野ではどのように使われているのかなど、
反射的に解けるだけ ではなく、自ら情報を判断し、整理する力が問われています。

じっくり取り組ませる問題の多い他の上位校に比べれば、
「算数が不得意でもなんとかなる」ということはありません。

ハイレベルな受験生の中では、すぐに差がつき ます。
灘中1日目なども同様ですが、
基本問題の基本たる所以をしっかりと考え、
噛締めていくべきだというメッセージが込められた良問です。