学習塾ロジム　今週の1問by 学習塾ロジム

今週 は筑波大付属中より1問です。

7／2　ｍのひもを切って、1／3ｍのひもをつくります。ひも は何本つくれますか。また、何ｍ余りますか。　　　 　　

商とあまりの単位。そして、割り算の意味をきちんと確認しましょう。

7／2 ÷1／3　　＝　21／2　　　　　　となる。
この割り算の商である　21／2　は、
7／2　の中に、1／3　が　21／2　本とれるという意味である。

つまり、きちんと　1／3　ｍとれたひもは10本であり、
それに　1／2　　本という足りないものがあまるということ。

1／2　　本＝　1／3　×　1／2　＝　1／6　ｍ

つまり、あまりは、　1／6　　　ｍとなる。

答え 10本とれて　1／6　　ｍ余る

ま さか、こんな簡単な問題に、、。と、
当時の優秀な受験生たちが何人も引っかかった問題です。
誤りはすべて、あまりを1/2としたものです。

割り算の意味「相当の計算」「分配の計算」をしっかりと理解し、
商、あまりの意味（＝単位）をきちんと意識できるのかどうかが試されました。

四則演算の意味を正しく理解していなければ、
中学以降の文字を使った数式中心の世界を渡っていけません。
特に難しく、奥の深い「余り」を中心にしっかりと意味を考える時間をとっておきたいものです。

～今回の問題から導かれる出題校からのメッセージ～
・ 「計算方法を知っている」ことと、
「計算の意味を理解している」ことは違う
・「筑波大附属は、基本問題中心だから、基本問題集を何度もくり返すべき」

本校に限らず、よく聞かれる浅はかな過去問分析です。
特にハイレベル校において、
「基本問題中心」とは、「計算問題や教科書的典型問題をスピーディーかつ正確に解かせる問題構成」という意味ではありません。

四則演算や図形の成り立ちなど、基本原理を活用して、複雑な問題を美し く解く。
と定義したほうが近いでしょう。

基本原理は、必ず（とくに小学校の教科書や塾の導入章において）説明されています。
その部分を飛ばして、表面的な演習（つまりとりあえず慣れろという方法論）に走る子どもたち（むしろ指導者たち？）に強く警鐘を鳴らす問題です。

例えば、ガウスの等差数列の和の公式と台形の面積の求め方の基本原理は同じです。
どちらも必ず習う公式ですが、基本原理の類似性をしっかりと理解していると、
この2分野以外でも応用のきく考え方になります。

折角たくさんの問題に取組むのです。帰納的に収斂させ、検証するという作業を加えることで、
高い仮説検証能力を身につけることに繋がります。
「基本事項からの出題」という縛りの中で、ハイレベルの受験生に対応してきた本校の問題は、
「基本」の大切さをきちんと理解できる生徒を選りすぐるのに適した良問となっています。

市川中より1問です。

下の図のようなおうぎ形OABがあります。このとき，次の問い に答えなさい。
（1）円周率は3.14とし、おうぎ形OABのまわりの長さを、四捨五入して上から3けたのがい数で求めなさい。
（2）円周率を3として計算すると，おうぎ形OABについて，いくつかの問題が起きます。この間題の1つを13字以上52字以内で説明しなさい。(市川中）

（２） は（１）を導入として使ってみましょう。

（１）弧AB＝2×3.14×1/6＝1.046・・・
よって半径2つ分を加えると
1＋1＋1.046・・・＝3.046・・・
うえから3けたのがい数に 直すと
3.05
よって
答え　 3.05平 方センチメートル

（２）
（１）におい て、求めた弧ABの長さは、円周 率を3とするｔ
2×3×1/6=1
となり、半径と 同じ長さになる。
つまり、おうぎ 円ではなく、明らかに正三角形となってしまう。

（１）を導入に使うことが、唯一の突破口。
あとは、何百回としてきた円の面積、周の計算をどのように見つめてきたかが問われました。

導入授業で最初に示された後、
ほとんど触れられることのない公式や定数の意味をしっかりと捉えなおす出題は、
超上位レベルの学校で 出されても低正解率になります。

しかし、数の性質と同様、普段何気なく処理し ている手法の仕組みは、
大学入試にまで応用が利くとても重要な考え方です。
3年、4年、5年で「初めて習ったときの説明」を再度確認してください。
勉強が進んだ後でも、大きな気付きがあるはずです。

～今 回の問題から導かれる出題校からのメッセージ～
・出会った知識を掘り下げる探求心こそがすべて

円周率3騒動
（実際は、円周率を3としてすべての指導が行わるという方針だったたわけではないのですが、
大騒ぎでしたね。）の時の出題です。

当時は、東大でも似たタイプの出題がありました。

「文科省への出題による抗議」という特異な時代背景を持った出題だと捉えず、
算数の勉強姿勢を正すきっかけとしてもらいたい出題です。

そもそも、円周率とは何の「率」なのだろうか。
円の面積を求める仕組みはどのようなものか。

小学生が知識として叩き込まれるものの成り立ちには、先人たちのとても柔軟な発想が寄与しています。

「身の回りのものを測量できればよい」という立場では、
これらはブラックボックスの中に入れたままにしても全く問題はないでしょう。
それどころか、余計な体力を使わずに済みます。

しかし、皆さんが進もうとしている中学校は、
数学を含め新しい知の枠組みを作り出す人間を育てようとしている学校です。

「とりあえず入学してから。」「まずは目先の試験。」といった姿勢は、
結局は入学後も続き、大学受験の訓練場としてしか中学・高校の場を活かすことができないでしょう。

何よりも、ものの成り立ち・背景・本質にこだわる。

この姿勢を身につけることは、志望校対策の何倍もの力を身につけさせてくれることでしょう。
当時も今も、過去問分析に奔走する関係者に、学校が本当に欲しい人物像を見せ付けてくれる良問です。

～今回の問題から導かれる出題校からのメッセージ～
・ 「計算方法を知っている」ことと、
「計算の意味を理解している」ことは違う
・「筑波大附属は、基本問題中心だから、基本問題集を何度もくり返すべき」

本校に限らず、よく聞かれる浅はかな過去問分析です。
特にハイレベル校において、
「基本問題中心」とは、「計算問題や教科書的典型問題をスピーディーかつ正確に解かせる問題構成」という意味ではありません。

四則演算や図形の成り立ちなど、基本原理を活用して、複雑な問題を美し く解く。
と定義したほうが近いでしょう。

基本原理は、必ず（とくに小学校の教科書や塾の導入章において）説明されています。
その部分を飛ばして、表面的な演習（つまりとりあえず慣れろという方法論）に走る子どもたち（むしろ指導者たち？）に強く警鐘を鳴らす問題です。

例えば、ガウスの等差数列の和の公式と台形の面積の求め方の基本原理は同じです。
どちらも必ず習う公式ですが、基本原理の類似性をしっかりと理解していると、
この2分野以外でも応用のきく考え方になります。

折角たくさんの問題に取組むのです。帰納的に収斂させ、検証するという作業を加えることで、
高い仮説検証能力を身につけることに繋がります。
「基本事項からの出題」という縛りの中で、ハイレベルの受験生に対応してきた本校の問題は、
「基本」の大切さをきちんと理解できる生徒を選りすぐるのに適した良問となっています。

今週は、昨年の巣鴨中入試から算数分野の一問です。

下の図 のようなおもてが1、3、5、7、9　うらが順に2、4、6、8、10と数が書かれている5枚のカードがあります。この5枚のカードのうち4枚を右下の （ア）、（イ）、（ウ）、（エ）の上に、おもてまたはうらにして置いて、正しい式を作ります。このとき、次の問いに答えなさい。

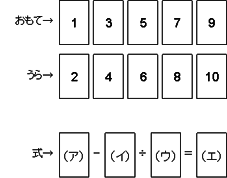
問１）（エ）における数のうちでもっとも大 きな数を求めて、
　　　そのときの（ア）、（イ）、（ウ）、（エ）に置ける数の例を一つ書きなさい。
問2）（エ）に置ける数のうちでもっとも小 さな数を求めて、
　　　そのときの（ア）、（イ）、（ウ）、（エ）に置ける数の例を一つ書きなさい。
（巣鴨中）

問題となっている部分にしっかりと注目して、作業することが大切です。
式に、1から10までの数を自由に入れるのならば簡単です。この問題を難しくしている要素は何でしょうか。

問１）（ア・イ・ウ・エ）＝（10・4・2・8）か（10・6・3・8）のいずれか 1つ。
問２）（ア・イ・ウ・エ）＝（3・10・5・1）のみ

問１）
（エ）に10を置くことはできません。
（ア）にも10を置き、（イ）÷（ウ）を0にすることは無理だからです。
（ア）から何かを引いてエになるのですから、エに最大の数字10は入りません）
また、9を置くこともできません。
（ア）に10を置き、（イ）÷（ウ）を1にしなくてはいけないのですが、
（イ）÷（ウ）を1にするということは、（イ）と（ウ）を同じ数にすることで、
それは不可能だからです。

このように（ア）に置ける数を大きいものから実際に代入して、試行していきます。
（エ）に8を置く場合を考えます。

・（ア）に10を置いて、（イ）÷（ウ）を2にする。
・（ア）に 9を置いて、（イ）÷（ウ）を1にする。

の2通りの方法が考えられます。

しかし、後者は（イ）÷（ウ）を1にすることが前述の理由で不可能なことから、不適合。
よって、前者を考えます。
（イ）÷（ウ）を2に出来る組み合わせは、
（イ・ウ）＝（2・1）（4・2）（6・3）（8・4）（10・5）
の5通りある。

しかし、（2・1）は、同じカードの表と裏なので不適、
（8・4）（10・5）は、それぞれ8、10をすでに使っているので不適となる。

よって、
（エ）に8を置いて、考えられる組み合わせは
（ア・イ・ウ・エ）＝（10・4・2・8）と（10・6・3・8）の2通り。
（エ）に可能なもっとも大きな数を入れた場合について問われているので、
（エ）に7以下を置く試行は行わなくても良い。
よって
（答え）
（ア・イ・ウ・エ）＝（10・4・2・8）か（10・6・ 3・8）のいずれか1つ。

問2）
問１と同様の考え方で、（エ）について小さいものから順に試行していく。
（エ）に1を置く場合を考える。

問１で判明している通り、（イ）÷（ウ）を1にすることは不可能であることから、
①（ア）に 3を置いて、（イ）÷（ウ）を2にする。
②（ア）に 4を置いて、（イ）÷（ウ）を3にする。
③（ア）に 5を置いて、（イ）÷（ウ）を4にする。
④（ア）に 6を置いて、（イ）÷（ウ）を5にする。
を考える。

これ以降は、（ア）を10以上かつ（イ）÷（ウ）を7以上にすることが明らかに不可能なため試行しない。
--------------------
①の場合、
（イ）÷（ウ）を2に出来る組み合わせは、
（イ・ウ）＝（2・1）（4・2）（6・3）（8・4）（10・5）の5通りあるが、
（2・1）は、同じカードの表と裏なので不適、 （6・3） 3そのもの、
（4・2）（8・4）は、4の表の3をすでに使っているので不適となる。
よって、
（ア・イ・ウ・エ）＝（3・10・5・1）のみ適合。
---------------------
②の場合、
（イ）÷（ウ）を3に出来る組み合わせは、 （イ・ウ）＝（9・3）のみ
これは、すでに3の裏である4を（ア）に使っているので、不適。
--------------------
③の場合、
（イ）÷（ウ）を4に出来る組み合わせは、
（イ・ウ）＝（8・2）のみこれは、すでに2の表である1を（エ）に使っているので、不適。
--------------------
④の場合、
（イ）÷（ウ）を5に出来る組み合わせは、（イ・ウ）＝（10・2）のみ
これは、すでに2の表である1を（エ）に使っているので、不適。
--------------------
以上より、（エ）に1を置いて、考えられる組み合わせは
（ア・イ・ウ・エ）＝（3・10・5・1）の1通りのみ。
（エ）に可能なもっとも小さな数を入れた場合について問われているので、
（エ）に2以上を置く試行は行わなくても良い。
よって
（答え）
（ア・イ・ウ・エ）＝（3・10・5・1）のみ

まず、（エ）を決めることがすべてである ことを見抜かなくてはいけません。
問題は、（エ）に最大・最小を置いたときに、それを成立させる（ア）（イ）（ウ）の一例を挙げろいうものなので、（エ）に大きな（小さな）ものから代入し ていき、それが不成立であることを確実に明らかにし、成立であることは部分的に（一例のみ）明らかにすればよいのです。

適当に（多くの場合（ア）への10の代入からスタート）探す生徒の多くは、

（１）の場合（10・9・3・7）を答えとして挙げます。

問題のルールの制約（数字が2つ表裏となっていて同時使用が不可能）を忘れ、左から大きなものを試行しているのです。

「問題は（エ）であること。」
「（エ）に入るものは10通りしかないこと。」
を考えると、代入して試行していくことがもっとも近道であることに気づかなくてはいけません。

また、このようなゲーム形式の問題では、
「ルールの中で、何かこのゲームを複雑にしているのか」
という視点で、問題文を読み解くことが重要です。

この問題は前述の通り、数字を自由に入れることが出来ない。（つまり1と2、3と4、5と6、7と8、9と10は同時には使えない）が唯一かつ最大の制約 です。ここに気付けば、正確なチェックをすることが出来ます。

3年生でも十分に解答可能な易問ですが、上位校特有の「読解力を問う作業問題」 は、不得意とする生徒の多い分野です。
国語読解力によって大きく差が開く分野の近年の広まりは、「コミュニケーション力」と「試行錯誤の中で規則を発見する力」という、旧来型の受身の受験勉強では力 がつきにくい能力を測ろうという試みです。社会では当然求められるこれらの能力に関しての
対策が求められるメッセージ性の強い良問です。

～今回の問題から導かれる出題校からのメッセージ～
・すべての基本は国語力である。

近年、上位校では四教科すべてにおいて「国語力ありき」の問題が多くを占めています。丁寧な読解力で、問題文の構造とメッセージを把握できなければ、全く手も足も出な いという設問です。その上で、基本的な知識の深い理解が問われています。

相手のメッセージ、構造、気持ちなどの、その場ではじめて与えられる条件にきちんと対応する能力。これは、机上での一般的ルールの習得とは一線を画すレベ ルの高い要求です。
社会人としてもっとも重要なこの「状況対応力」を求める上位校の傾向こそが、上位中学校受験が「精神的に大人であるこ と」が要求されているとされる所以でしょう。

かつて（今でも？）「とにかく復習重視。一度見た問題は絶対に間違えない。」という反復によるパターン認識力向上が叫ばれた受験勉強ですが、こと上位校に 関しては、その傾向のの偏重に一石を投じる意味で、この分野の出題の広まりは続きそうです。

複雑な文章題に丁寧に取り組む時間を低学年時からしっかりととることが重要です。

・具体的に手を動かし、試行錯誤する中でイメージをすることが重要
ルールがどのような制約を与えるのか。
それは、具体的に試行錯誤することで、実感できます。本問では、（エ）に数字を代入して、それを成立させるものを探して更に代入してみることです。

「問題をひたすらにらみ続けている」
「ノートがあまりにもきれい（試行錯誤の痕跡がない）」

は、このような問題に太刀打ちできない生徒の行動の典型例です。
とにかく、具体的なイメージを把握することが先決。そのための行動力は必須能力です。
「例えば～」と適当な試行をしてみる習慣 をつけることが大切です。
「実験と考察を同時にすばやく行う力」は理系に強いといわれる学校では必ず問われる能力です。