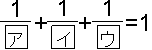学習塾ロジム　今週の1問by 学習塾ロジム

簡単な虫食い算ですが、論理的に解いてみましょう。

次のア、イ、ウに入る数字を答えなさい。

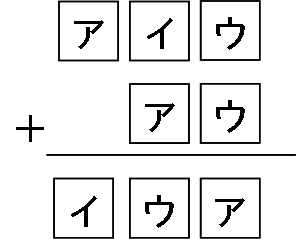
アとイの数字の関係に着目するところからスタートです。
　

百の位のアの下に、アとは異なるイがきているということは、繰り上がりによって数字が変わっていることになります。

2つの数字の足し算ですから、繰り上がりとして考えられるのは1のみ。
つまりアに1を足すとイになることがわかります。・・・(1)

次に１の位の足し算に注目します。ウ＋ウはアとなっています。
これはウ×2の一の位がアと考えると、アは偶数であることがわかります。・・・(2)

(1)、(2)より（ア、イ）の組み合わせは（0、1）（2、3）（4、5）（6、7）（8、9）です。
※0が偶数かどうかは議論がありますが、アの候補として0が挙がることは理解できるでしょう。

ここで十の位の足し算に注目します。イ＋アは、(1)で考えたように繰り上がらなくてはいけませんので、
足すと10以上ということになります。つまり上の候補の内、適当なものは（6、7）と（8、9）の2つのみとなります。

この2つを検討します。

（6、7）だと、一の位の足し算に注目して考えられるのは3もしくは8。3で673＋63＝736で正解。
8は十の位で6と7の和13の一の位3に繰り上がりの1を加えても4にしかならないので不適。

（8、9）だと、一の位の足し算に注目して考えられるのは4もしくは9。4だと十の位で8と9の和が7となり不適。9はすでにイで使われたため不適。
よって答えは673＋63＝736の一通り。

答え：ア：6、イ：7、ウ：3

2年生クラスの問題でした。説明まで出来た生徒は少なかったのですが、
当てはめで偶然に出来たというレベルから一歩進んで説明ができるようになると、
数の持つ性質、規則への配慮が行き届くようになります。

虫食い算の説明を書くというのは四則演算のそれぞれの仕組みについて考えるのには絶好の教材です。
数学の女王「整数」の入り口として、是非活用してください。

筑波大付属中より。問題文を読む姿勢が問われます。

算数のテストの得点を調べたら、0点の人は1人もいませんでした。また、田中さんの得点から中村さんの得点をひいた差が、ちょうど山本さんの得点と同じになりました。次のうち、正しいものはどれでしょう。

（ア）田中さんの得点は、中村さんの得点と山本さんの得点の和よりも多い。
（イ）田中さんの得点と山本さんの得点の和がちょうど中村さんの得点に等しい。
（ウ）中村さんと山本さんの得点はどちらも田中さんの得点より少ない。
（エ）田中さんの得点と中村さんの得点の和がちょうど山本さんの得点に等しい。

(筑波大付属中）

「差」を扱う問題の定石手法が突破口です。

問題文の
「田中さんの得点から中村さんの得点をひいた差がちょうど山本さんの得点と同じになりました。」
を線分図で表すと下記の通りとなる。

よって
ア：田中さんの得点と中村さん、山本さんの得点の和は等しいので誤り
イ：田中さんの得点は一番高いので明らかに誤り
エ：田中さんの得点は一番高いので明らかに誤り

答え：ウ

不等式など、関係性を数式処理によって表して処理しようとすると複雑になり、
時間もかかってしまいます。

問題文の「差」という表現に着目し、線分図によって整理するという定石手法によって問題の整理が一気に進みます。

旅人算などもそうですが、与えられた情報を見やすい形に整理して、
より多くの情報を引き出すという姿勢をもっていることが必要となる問題でした。

～今回の問題より導かれる出題校からのメッセージ～
問題文の条件の図式化が大切

線分図をはじめとして小学生では「～図」に整理するという手法を数多く学びます。

方程式にとってかわられるという理由で避けてしまう指導者、生徒も多いのですが、
この図式化によって学べることは、方程式によって学べることとは異質のものです。

式の処理によってだけでなく、図にして幾何学的に考える作業というのは高度な数学の能力として必要となるものであり、
なにより数の性質を多面的に捉えることになる魅力的な手法です。

現実問題として、昨今の入試問題では、
方程式で処理した場合時間がかかりすぎてしまう仕掛けがされることも多くなっています。

小学生ならではの様々なものの捉え方を楽しむ姿勢が必要です。
洗練された図式化により一気に解ける。図式化の価値と面白さを教えてくれる良問でした。

灘中より。非常に短い問題文を整理する国語力が問われます。

ある5桁の整数があります。この整数には、数字0がA個、数字1がB個、数字2がC個、数字3がD個、数字4がE個使われていて、これ以外の数字は使われていません。また、この5桁の整数は一万の位から順にABCDEとなっています。ABCDEの中には同じ数字があってもよく、BCDEは0であってもよいものとします。この5桁の整数を求めてください。

(灘中）

紛らわしいかたちで与えられている2つの条件を整理しましょう。

A、B、C、D、Eは、それぞれ5桁の整数の中で、0、1、2、3、4の数字が使われている個数ですから、
A＋B＋C＋D＋E=5です。

また、Aは5桁の数の先頭なので1以上です。
これは、Aは数字0の個数も表しているので、同時に数字0も1個以上あることを意味します。

0が1個以上あるということより、1、2、3、4の数字はあわせて4個以下しか使われていません。
さらに、その使われているA、B、C、D、Eの合計は5と決まっているので5つの数字の組み合わせは、

（0、0、0、1、4）（0、0、0、2、3）（0、0、1、1、3）（0、0、1、2、2）（0、1、1、1、2）

の5通りしかありません。

この中（0、0、0、1、4）は、「4」に着目すると、4つ使われている数字は明らかにないので不適。
同様に（0、0、0、2、3）も「2」に着目すると不適、
（0、0、1、1、3）も「3」に着目して不適、
（0、1、1、1、2）も「2」に着目して不適。

よって（0、0、1、2、2）を問題文の条件どおりに並び替えた21200が求める数になります。

答え：21200

短い問題文ですが、題意を非常にとらえにくくなっています。

「5桁の数ABCDEの各位の数A、B、C、D、Eは、
同時にA、B、C、D、Eの中にある0、1、2、3、4の数字の個数を表している。」

という分割して考えにくい2つの条件を整理して、チェックする姿勢にたどり着けるかどうかが分かれ目になっています。

後半の条件は数式化しやすく（A+B+C+D+E＝5）、
それを土台にして前半部分の突破口である「Aは1以上、
同時に0は1個以上」から手をつけていきます。

～今回の問題より導かれる出題校からのメッセージ～
日本語で書かれた見にくい条件文をきちんと理解し、整理することが必要です。

灘中の入試では、非常に短い問題文の中に隠されている複数の条件を、「使える形」で瞬時に整理する力が問われます。

コツは、どの日本語を既に使ったかどうかを明確にしておくことです。

本問では、ほとんどの生徒が、まずA+B+C+D+E＝5という条件を見つけることになるとおもいます。
ここで問題文を離れ、書き出しや当てはめを始める生徒がよく見られますが、
「問題文の5桁の数は一万の位から順にABCDE」を処理できていないのです。

一つ一つの日本語を精査する読解力。

算数の短問の中においても重要となるのはやはり国語力です。

東邦大学付属東邦中より。概算と精査の組み合わせです。

となるように、□の中に1から9までの異なる整数をあてはめます。このとき　ア、イ、ウ　の合計はいくつになりますか。

ア、イ、ウが同じ数だとしたらいくつになるでしょうか。

ア、イ、ウが同じ数だとしたら３です。

つまりア、イ、ウが異なる場合、すべて3以上の数にすると合計が1に満たないことになります。
（例えば1/3+1/4+1/5は1に満たない。）

よって、ア、イ、ウのうち一番小さい数は2であることがわかります。これをアとします。

よって残りの2つの分数の和は1/2となります。

ここで、先程と同様にイ、ウが同じ数だとすると4となります。
つまりイ、ウが異なる場合、ともに4以上の数にすると合計が1/2に満たないことになります。
（例えば1/4+1/5は1/2に満たない。）

よってイ、ウのうち小さいほうの数は3となります。
これをイとすると、ウは6になります。
3つの数の合計は2+3+6=11

答え：11

初見だとしたらかなりの難問です。

「同じ数だとしたら」すべてが3となること。
3つ異なる数ですから小さい順にア＜イ＜ウとなること。

そこから最初の2を見つけることが突破口です。
与えられた条件をひとまず無視して計算をして、そこから条件にあわせて微調整していくという手法はつるかめ算などにも共通する技術です。
まずは「概算」で見通しを立てる。
方程式の通用しにくい中学入試ではとても大切なステップです。

～今回の問題より導かれる出題校からのメッセージ～
概算と精査のバランスが大切

本問のように一気に答えを算出する方法がない問題は、中学入試では多数出題されています。

ひたすら書き出していくしかなかったりするものもすくなくありません。

そんななかでも、書き出しの量を減らす工夫はとても大切です。

大雑把に答えの周辺にあたりをつけてみることで、明らかに不要な部分を省略することができます。
また、とりあえずの計算をしてみることで、答えが大体どれくらいの範囲におさまりそうなのかということも把握することができます。

「とりあえずやってみる。」

闇雲な第一歩がゴールへ近づく近道となります。

栄光学園中より。与えられた条件の意味を掘り下げる力が問われます。

20名のあるクラスで次のような方法で席替えを行いました。
（１）くじで２人１組のペアを１０組つくる。
（２）そのペアになった２人の間で席を入れ替える。
（３）（１）、（２）をもう一度くりかえす。
席替えをした後も席替えをする前と同じ席に座っている生徒が１１名になることはありえません。その理由を答えてください。

(栄光学園中）

ありえないとされる「１１」という数字の特性に着目してみましょう。

１回目の（１）（２）の席替えで必ず全員が自分の席を離れることになる。
２回目の席替えを考える。

ある人が元の席に戻るためには、
１回目終了時点で元の自分の席に座っている人、
つまり１回目の席替えでペアになった人と２回目の席替えでもペアにならなくてはいけない。

このとき、相手も元の席に戻ることになる。
つまり、２回目の席替えである人が元の席に戻るということは、
１回目の席替えの相手も元の席に戻ることを意味する。
よって２回目の席替え終了時点で、
元の席に戻る人数は必ず２人の倍数になるので問題の「１１人」は該当しない。

「どんな方法によっても」１１人がありえないことを説明するというのは、コツが必要です。

A）すべての方法を試して１１人という結果がないことを示す。
B）「１１人」という個別の数字ではなく、
「奇数はありえない」「過半数はありえない」など「１１」のもつ特性に着目して証明の目標を緩くして論証する。

のどちらかです。
A）を稚拙だと決め付けてはいけません。高々数十通りの可能性であればそのほうが完結な場合もあります。
今回は、B)です。ほとんどの受験生が２回の席替えの場合の数はかなり多いことを容易に想像すると思いますので、
B)の方針で検討したことかと思います。

「すべて」「かなら」の証明にはある程度の習熟が必要ですので、
身の回りや通常のディスカッション・説明の機会を活かしていくことが大切です。

～今回の問題より導かれる出題校からのメッセージ～
論点を適宜変形していく力が大切

証明は中学生の範囲ですが、
論点の整理と論証の方向付けの能力というものは小学生に対しても十分に問うことの出来る分野です。

本問で問われているのは
「とあること」を証明するということは、何を意味するのか。
ということを掘り下げる力です。

直接は説明できなくても、同じことを意味するものを見つけ出し、
そちらの説明へと方針を転換する。

身近なものでは対偶をつかった証明など「間接的な」証明能力が問われる場面は少なくありません。

与えられた条件を様々な角度から検討し、知識を動員して同値なものに確実に変形していく力は、
未知の問題を身近な問題に引き寄せる能力としてまさに応用力そのものと定義できます。

本問はその力を測る良問ですし、同じ形式を出題し続ける本校が最も大切だと考える能力であることを宣言している問題ともいえます。

高槻中学校より。「作業の概算」で手法を取捨選択します。

0より大きい4つの整数a、b、c、dがあります。
a×b=28 ｂ×c=126 c×d=45　のとき、a、b、c、dの値を求めなさい。

(高槻中）

どこから「しらみつぶし」に取り掛かるかによって、作業量がかわります。

a＝２、b＝１４、c＝９、d＝５

ヒントにもあるように、選択肢の絞込みの際、最初の一歩を慎重に検討することが大切です。

a×b=28にのみ着目してスタートすると、
（a,b）の組み合わせは (1,28) (2,14) (4,7) が候補になります。

しかし、次のb×c=126の126を素因数分解すると2×3×3×7なので、
bの候補は1、2、7、14が残ってしまいます。

逆にc×d=45に着目すると(c,d)の候補は(1,45)(5,9)になります。

この中で126の因数となりうるのは1と9だけですし、
bは明らかに2桁の数なのでc=1は候補からはずれ、c=9が確定します。

どちらからスタートしても答えにたどりことは出来ますが、
スタート地点で少し立ち止まって考えるだけで作業量を減らすことができます。

～今回の問題より導かれる出題校からのメッセージ～
作業量を概算し、見通しを立てるという思考が大切

本問では大きな差はでませんが、解説にあるような「作業量の概算」はとても大切な技術です。

時間制限のある試験において、そもそもその手法の作業量に現実味があるのかどうかを判断する力です。

不適格であれば、他の手法を探すことになります。
このような効率的な状況判断をもたらしてくれるのが「作業量の概算」です。

解説を読んでみると、「書き出せば一番速かった。」ということや、
「既に書き出してはいたがそもそも無理な量だった。」という経験が誰しもあるかと思います。

見通しを立てる冷静な思考によって、必要となる時間が大きく異なってくる良問でした。

ラ・サール中より。「割り算」の仕組みの理解力が問われます。

下の（ア）、（イ）にあてはまる数を求めなさい。

13時35分（ア）秒÷18＝（イ）分18秒

(ラ・サール中）

割り算の筆算の仕組みを思い出しましょう。「位ごとに分ける作業をする」です。

（ア）を18で割った答えは、（イ）の部分には影響しない。
よって
13時45分＝815分から
815分÷18＝45.2777・・・
ゆえに（イ）は45

すると
13時45分（ア）秒÷18＝45分18秒
となる。
つまり
45分18秒×18＝13時45分（ア）秒
（ア）＝24

答え：（ア）24、（イ）45

割り算の筆算は、百の位の数、つまり百のかたまりをいくつかに分け、次に十の位の数字分の１０のかたまりをまた分ける。
という作業の繰り返しです。

分ける作業を位ごとに毎回行っているのです。

今回でいえば、13時を18で割った答えと、45分を18で割った答えと、

（ア）秒を18で割った答えを足し合わせたものが答えつまり商になるのです。

そう考えれば（ア）は60秒未満ですから18で割ってもその答えは4秒未満です。

すでに商には18秒がありますから、（イ）の部分に影響は与えていないことがわかります。

（ア）がなかったとしても商は（イ）分～秒なのです。

～今 回の問題から導かれる出題校からのメッセージ～
「数える」手段に対する深い理解が大切

本問のような割り算の考え方は、筆算の仕組みに対する深い理解が背景にあります。

そもそも四則演算の筆算は、「位ごとの数をかたまりとして扱う」ことです。

機械的に行えるだけでは、せっかく時間をかけて身に付けた筆算の技術を応用できません。
きちんとその構造を理解することで「効率よく数える」ことの意味を理解し、
正確で迅速な数え上げの技術が身に付くのです。

まずは、3年生レベルの筆算の仕組みから。

低学年の生徒にも説明できるようにしておくことは、必ず役に立ちます。
一行問題ですが、真の計算力を測る良問でした。

栄光学園中より。他者への説明とは何なのか。真っ当な論理性を問う良問です。

下の図の8つの空欄に、それぞれ異なるように整数を1つずつ入れていきます。このとき、空欄に入るどの数もその両隣の数の平均にすることができますか。理 由をつけてこたえなさい。

(栄光学園中）

とあることが「出来る」ことを説明するには、例を1つ挙げればよいのです。「出来ない」ことを説明するには、す こし考えなくてはいけませんね。

できない。

（理由）
異なる2つの数ＡとＢの平均の数は、
Ａ＞ＢのときＡより小さく、Ｂより大きい数である。

またＡ＜ＢのときＡより大きく、Ｂより小さい数となる。
つまり空欄の中にある異なる整数のうちの1つを考えたとき、
両側の数の平均であるということは、左右どちらかの数よりも大きく、
どちらかの数より小さいということになる。

しかし、8つの空欄にすべて異なる整数を入れるとき、
必ず「最大の数」が存在する。
その両側には、その数よりも小さい２つの数しか置くことができず、
間の最大の数をより小さな2つの数の平均にすることはできない。

以上の理由よりすべての空欄に異なる整数を入れ、
そのどの数も両隣の数の平均にすることはできない。

可能と不可能の説明は、
小学生の論理 性をはかるには格好の題材となります。

可能の証明は1つの例を挙げて終わりです。

ただし、不可能の説明には、高度な論理性が求められます。

反例を何個挙げても十分に説明したことにはならないということを、
事例を挙げながら理解させることが大切です。

これは中学生以降の証明問題への耐性を鍛えることに通じます。

類題を元にして、
教師、保護者の方々がしっかりと時間をかけて
説明することが必要な領域になります。

教室内で見られた別解として、
「1つの数ＡＣ の平均Ｂに関して、ＡとＢ、ＢとＣ の差は等しい。
するとＣ の隣のＤとその隣のＥとの差もそれぞれ等しくなり
8つの数の隣の数との差はすべて等しくなってしまう。・・・」

も上で解答として挙げたものとほぼ同数でした。

～今 回の問題から導かれる出題校からのメッセージ～
論理性に対する高い意識が大切

「自 分の立てた命題を、説明するために必要な要素は何なのか。」

中学生以降の高度な勉強、そして研究に関して、
これを見つけ出す感覚ほど重要であり、必要とされる素養は他にないといってもよいでしょう。

現在の中学受験のための塾の授業形態は圧倒的に
「インプット→自習による定着→テスト」というスタイルがとられています。

しかし、中学生以降の高いレベルの勉強において「答え」のみを提示し、
その正誤のみで評価されるような機会はほとんどありません。

入試に出ない から、などという理由で他者に対する説明能力を鍛えないことは、
入学以降の勉 強姿勢に大きく影響します。

またこの能力は普段から意識していなければ伸びることはありません。

本問は、東京大学など入試のほぼすべての問題が記述形式であり、
高い説明能力が求められる学校への合格率において、
圧倒的な結果を残している本校が求める人物像が見て取れる良問だと言えるでしょう。

城北中より。「身の回りの算数」に向き合う姿勢が大切です。

ある月の月曜日の日にちの数字の和が６６のとき、この月の2日は何曜日でしょうか。

（城北中）　　　　　　

同じ曜日の日付には、大きな制限が存在します。

同じ曜日の日付は、前の週＋7日となっています。
つまり
1週目をX日とすると
2週目：X＋７
3週目：X＋７＋７
4週目：X＋7＋7＋７
5週目：X＋7＋7＋7＋7
となっているのです。
ここで、Xが何日であれ、5週目まであるとすると、そこに含まれる「７」の数は10個となり、
日付の和は「X×５＋70」、つまりXが1日でも日付の合計は75日になるのです。
今回、考える月曜日の日付の和は66なので、この月に月曜日は4日しかなかったことがわかります。
よって4週目までの日付の合計の式より
X×４＋７×６＝６６
となり、Xつまり1週目の日付は6日です。
6日が月曜日の月では、2日は木曜日となります。

答え：木曜日

今週の一問でも何度か取り上げた
「問題文では明記されていないあたりまえの制限を活用する。」
問題です。

今回の「日付」は、その中でもよく出題される題材です。
初見の場合、「日付の合計だけで曜日が決まってくるのか。」という壁にぶつかります。

通常の塾のカリキュラムでは、連続する整数の和など類題も数多く学ぶことになりますが
このタイプの制限は、見た目を変えて出題しやすくまた、問題文の中に埋もれて見にくくなっています。

整数倍や人数と比などの形で抽象化してまとめておかなければ、
なかなか気づけるほどの認識力は身につきません。
解答を読むと、「気づかなかった」というレベルで済ましてしまいがちですが、
日ごろのまとめる作法が問われる問題です。

～今回の問題から導かれる出題校からのメッセージ～
「身の回りの算数」に向き合う姿勢が大切

本問に一度取り組んでおけば、類題は問題なく解けることになります。

しかし、本問を通して学ばなければならないのは、
「問題文の日本語に隠された数学的な意味を探りながら読む習慣」
の大切さです。

算数や数学を使ってとくべき問題は、身の回りにたくさんあります。
しかし、その問題は数式によっては与えられていません。

「算数として考えると・・・、数学的に考えると・・・」という普段からの問いかけだけが、
日本語として与えられる条件と数式を行ったりきたりする能力を育みます。

カレンダーという身近なものに含まれる算数を探求させる本問は、
問題を離れた世界で数学的思考の適用力を測る良問です。

東大寺学園中より1問です。

4個の円（ア）、（イ）、（ウ）、（エ）が図１のように交わ り、10個の部分に分かれています。
　この10個の部分に0、1、2、3、4、5、6、7、8、9の数字を、同じものを2度使わないように、しかもそれぞれの円の中の数字の和が同じ値（Aと する）になるようにわりあてます。例えば、図1のようにわりあてると、
　円（ア）の和は9＋0＋3＋4＋7＝23
　円（イ）の和は0＋3＋2＋6＋7＋1＋4＝23
　円（ウ）の和は3＋4＋8＋2＋6＝23
　円（エ）の和は4＋7＋6＋1＋5＝23
となり、A＝23です。


（問）　図2の□の中にそれぞれ数字を当ては めなさい。

　　　　　　　　（東大寺学園中）

ノーヒントです。

図 ３のように、分かれている10個の部分にB ～Kの記号をつける。
円（ア）の中の数字の和は、B＋C＋D ＋E ＋F
円（イ）の中の数字の和は、C＋D＋E＋F＋H＋G＋K
円（ウ）の中の数字の和は、D＋E＋G＋H＋I
円（エ）の中の数字の和は、E＋F＋G＋K＋J

それぞれの円の数字の和の合計は等しいことに着目すると
円（ア）の合計＝円（イ）の合計より
共通部分のC、D、E,Fを除いた、B＝H＋G＋Kである。

ゆえに求めるべき数字の一つ（上の□）B＝2＋7＋0＝9
円（イ）の合計＝円（ウ）の合計より、
共通部分のD、E、G、Hを除いた　C＋F＋K＝I

ゆえに求めるべき数字の一つ（左下の□）I＝3＋5＋0＝8
円（イ）と円（エ）も同様に考えると
共通部分のE、F、G、Kを除いたC＋D＋H＝J

ゆえに求めるべき数字の一つ（右下の□）J＝3＋1＋2＝6
となる。

複 数の要素から成立しているものどうしを比較する問題です。

低学年のときに、天秤で勉強した内容の発展形です。
複数の要素から成立しているものの比較のポイントは、

「差に関係している要素はどれか」

について、正確に把握することです。

それ以外のものは視界から外す、つまり引いてしまっても問題ありません。
また、正確に把握できていれば、双方に同値のものを加えて変形させて考えることもできます。

今回は、それぞれの円の値となっている要素をきちんと列挙して、検討することが
突破口になります。低学年の教室でも正答率は高くなりました。

～今 回の問題から導かれる出題校からのメッセージ～
隠れた制限に対する探究心が 大切

魔 方陣など、一見当てはめで解けそうな問題にも、
論理的な突破口を検討する姿勢は入学後の勉強の姿勢として
強く求められるものです。

「答えを狭める要素は何かないのだろうか。」

無限に広がって見える選択肢を前にして
立ち止まりとことん考え抜く姿勢を持ったものだけが、
正答にすばやくたどり着くことができます。

答えを得ることだけが本番では大切です。
しかし、本問は、

普段の勉強の中でプロセスを大切にしてきた生徒と
そうでない生徒との間に明確な差

が生まれるようなボリュームで設計されている良問だといえます。