学習塾ロジム　今週の1問by 学習塾ロジム

今週は女子学院・算数入試問題からの1問です。

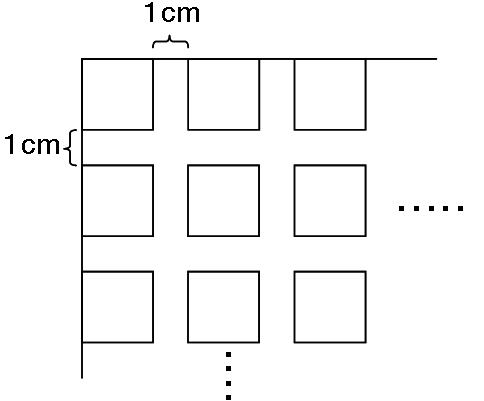
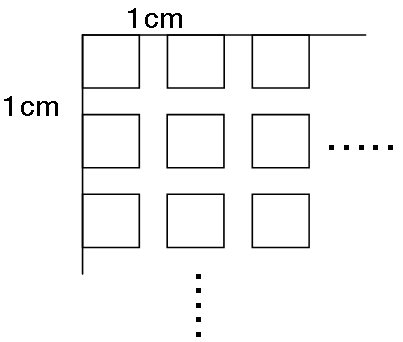
たて 135ｃｍ、横183cmの長方形の場所に図のように１cmの間をあけて、正方形のタイルをしきつめよう
と思う。タイルのしき方は４すみとも図のようになる。できるだけ大きな正方形を使うとすると、タイルの一辺は何cmになるか。また全部で何枚のタイルが必 要になるか。　　　　　　　　　　　　　（女子学院）

「公倍数・公約数」の範囲で、とても似た問題に必ず出会っているはずです。それらとの差は何なのでしょう か。

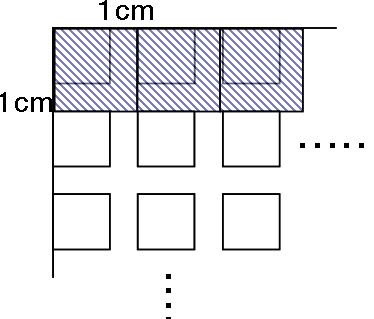
図２のように、隙間までふくめた正方形のタイルを敷き詰めることをかんがえる。
長方形のたてとよこをそれぞれ１ｃｍずつ広げて考えれば、
ここで算出された正方形のタイルの１辺が、
「求めるべきもの＋１ｃｍ」となり、
敷き詰められた枚数が、求めるべき枚数になる。
よって、
たて：135+1=136
よこ：183+1=184
という長さの長方形に隙間なく、正方形のタイルを敷き詰めることを考える。
この２つの数の最大公約数は8
よって、図２のように考えたときの正方形のタイル（斜線のもの）の1辺は8ｃｍ
これを図１で考えると、求めるべき正方形のタイルの1辺は
8-1=7
答え　 7ｃｍ

また、このとき必要となる正方形のタイルの枚数は
（136÷8）×（184÷8）＝391
答え391 枚

「たて、よこがそれぞれ15cm、18cmの長方形をなるべく大きな正方形に切り分け、余りがでないようにするとき、正 方形の1辺は何ｃｍになりますか。」
4,5年生が勉強する「公倍数・公約数」の範囲で、
最大公約数の考え方をつかった問題として必ず取り組む練習問題です。

本問とこの問題の類似性に気付き、違いを考えることがスタートとなります。

解き方、つまり隙間の処理の仕方は解答で示した1通りだけではありません、大切なのは
「邪魔な隙間をどうにかして処理することで、最大公約数の簡単な問題に変形できないか。」
という工夫に、時間をすべて費やすことです。

その中から、解答例のような処理のしかた等が、導かれるのです。

この問題を難しくしている要因はなにか。
言い換えれば、
この問題はどの基本問題を難しくしているのか。
という視点は、問題の本質を見抜く力として求められる技術です。

～今回の問題から導かれる出題校からのメッセージ～
・基礎知識をベースに、走りながら情報を取捨選択する瞬発力のある思考が大切

基本問題が多く、比較的高得点の争いになるのが女子学院中学校です。
しかし典型問題であっても、必ずひねった部分を付け加えることも忘れていません。

こうした問題をすばやく解き進めることのできる生徒は、
どこまでが基本でどこが解答を導きだす上でのボトルネックとなっているのかを判断する能力に長け、
余計な情報に時間をとられることがありません。

逆に、間に合わない生徒は、余計な情報の整理に時間がかかってしまうのです。

よく言われる処理能力とは、「鉛筆のスピードが速い、計算が速い」だけでなく「情報に対する優先順位付けがうまい」というものが含まれます。

典型問題が解説できるレベルまで完全に習得されていること。
そして、とりあえず思考を進めてみてボトルネックを確認すること。

じっと立ち止まって一本道の解答を検討するだけではなく、
すぐに走り始め、判断をし、余計な情報をそぎ落としながら解き進めるという思い切りの良さ。

女子校としては特に際立ってこの傾向が顕著な
女子学院中の求める人物像が見て取れる問題となっています。

今週は、灘中入試から算数分野の一問です。

６桁の 整数　5ABC15　が999の倍数となるとき、３桁の整数　ABC　を求めなさい。

（灘中学校）

「999の倍数」とは、どのような数なのか？について考えることが出発点になります 。

5ABC15は999の倍数であることから、
5ABC15＝999×□と表すことができる。
この□に入る整数を探しだす。

まず、□は3桁の数である。

なぜなら、

1.最大の2桁の数99を代入しても6桁の数にはならない。（答えは98901となる）
2.最小の4桁の数1000を代入しても、999000となり、問題の数をこえてしまう。

からである。

それでは、この3桁の数を考える。
まず一の位が5であることが確定する。
5ABC15の一の位が5であることから、
999の一の位の9と、□の一の位を掛け合わせた場合の
商の一の位が5となることがわかる。

よって、
□の一の位は5となるのである。

このことから、
百の位も5となることがわかる。
なぜなら
百の位が6だとすると、
□が最小の605の場合でも999×605＝604395となり不 適。
また百の位が4だとすると、
□が最大の495の場合でも999×495＝494505となり不 適。
だからである。

この時点で5ABC15＝999×５☆５　と置くことができる。
以下、☆に0から数字を代入して調べる。
☆＝０のとき…504495
☆＝１のとき…514485
☆＝２のとき…524475
☆＝３　，　☆＝4，　・・・・・・・・・・
☆＝８のとき…584415
（☆＝８を代入して初めて　5ABC15　というカタチになる）
よって、ABC＝844　　　　　答え　844

虫食い算の典型問題です。

1.概算で桁数を判別する。
2.九九の答えの特徴についての知識を活かす。

という2つの作業で、桁数すらわからない「□」を見つける労力が大幅に減ります。
いずれも、虫食い算の基本的な作業です。

このように、ある数を計算ではなく
数に関する知識で求めなくてはいけない問題は実は多くありません。

知識を使わなければ、「数式化⇒算術による計算作業」では、試験時間を超える膨大な時間を要し、まったく手も足もでないという状況に陥ることも事実です。

実は、この2つの作業は、「正確で迅速な計算力」を支える大きな柱です。

小数の計算における小数点の打ち間違いは、
概算によってほぼ確実に避けることができます。

本番ではあまり出題されることのない虫食い算ですが、
本問は、計算問題や数の性質の重要性について考える
良い機会となるメッセージ性のある良問といえるでしょう。

灘中をはじめとする上位校の計算問題は、単純な反復練習だけではなく、数の性質について日ごろから注目し、考察を重ねながら解いてきたかどうかで大きな差 が生まれます。低学年でも太刀打ちでき、とても多くのことを学べる内容ですので、是非取り組んでみましょう。

～今回の問題から導かれる出題校からのメッセージ～
・定義・仕組みの根本的な理解が大切

灘中学校の1日目は、

膨大な量を適切にこなす正確性とスピードが問われる問題構成となっています。

それをこなすには、反復練習で身に付けたスピードだけでは太刀打ちできません。

基本知識の深い理解からのみ導き出せる洗練された解法で、
簡潔に解き進めなくてはいけません。

普段何気なく活用している、公式や知識は結果にすぎません。

それぞれの背景について、
しっかりと説明することができるのかどうかが問われています。
良く使う簡単な知識ほど、その背景を忘れてしまいがちなのです。

.本問では、もっとも基本的な、「九九と計算」に関して問われています。
「一の位が5になる九九を挙げてみよう！それらに共通点や規則性はあるかな？」
小学校2年生のクラスで必ず取組む問題です。

この知識を忘れてし まうだけでなく、いつのまにか解説という結果だけを吸収しようする姿勢になってしまっていては、本問にはもちろん、上位校の問題、そして入学後の勉強にも 対応することはできないでしょう。

掛け算や割り算の筆算や、つるかめ算や差集め算などの算術を中心に「なぜその方法で答えがでるのか？」について考えた り、九九、分数などの仕組みについてもう一度復習してみることはとても大きな意義があることでしょう。

「2つの三角形が相似ならば・・・」
についての知識はとても確かなものになっているかと思いますが、
「2つの三角形が相似となる条件」
について正確に挙げることのできる生徒は意外なほどに少ないのです。

今週は、昨年の海城中入試から算数分野の一問です。

掛け算 九九の表の答えのひとつひとつを４で割って、割り切れるなら青、1余るとき赤、2余るとき黒、3余るとき緑で表のマス目をぬ ります。
（１）このとき、一番少ない色は何色ですか。また何個ですか。
（２）５の段で一番多い色は何色ですか。
（３）３とかけて、答えの欄が黒になるマス目は何個ですか。　　　　　　　　　　

（海城中）

今回はノーヒントです。小学2、3年生でも取り組むことのできる問題です。
九九の表を書き出してみれば、簡単です。実際塗りつぶしていく中で規則を見つけてみましょう。

（１）緑　１２個　（２）赤　（３）６個　（1×2、2×1、2×3、3×2、1×6、6×1）

短時間での綿密な作 業が求められるだけではありません。このような「数の性質」の問題は、初見で解くのがとても難しい分野です。
典型問題の暗記で はなく、数を見る視点を自分の中に蓄えておくことが重要です。

4で割り切れる数→4の倍数
4で割って1余る数→最小が1で、その後5、9、13、といったように4×ｎ＋1で出現
4で割って2余る数→最小が2で、その後6、10、14、といったように4×ｎ＋2で出現
4で割って3余る数→最小が3で、その後7、11、15、といったように4×ｎ＋3で出現

と整理して、格段ごとに調べていくことも出来ますし、具体的に4の段まで手を動かしてみれば、その規則を容易に発見することができます。
本問は作業が面倒なこと以外は難しくない低学年でも解ける易問ですが、九九の表から、様々なことが学べるということを知るきっかけとなる良問です。

九九を違った視点から捉えなおすことをテーマにした問題は頻出です。
・1の位が0になるのはどのよう場合か。
・そもそも九九の表には答えは何種類あるのか。
・1～9の倍数は、それぞれどのような特徴があるのか。

など、様々なテーマが考えられますし、毎年出題されています。
ひとつひとつを覚えるのではなく、日ごろから数字を様々な形に分解してみたり、見た目を比べてみるなどの習慣が、数へのセンスを高めていきます。

～今回の問題から導かれる出題校からのメッセージ～
・結果 をさまざ まな視点でグループ分けする考察力が重要
　計算のスピードを上げることが、九九の暗唱の目的ではありません。九九の表から規則性を見つけてみようと試みることで、様々な角度から考察する力が身に つきます。本問は「余り」による分類です。

　また、状況に合わせて、その場で多くの視点を試すスピードも大切です。ひとつの結果 や常識に対して、絶えず違った視点から考察を試みる姿勢が求められて います。
算数の分野としては、
算術だけでなく、数学的センスの基本である数に対する意識を高めてもらいたい
というメッセージの込められた出題です。

また算数に限らず、目の前の当たり前の現象を、違った角度で捉えなおす姿勢というのは、理系教育に力を入れている海城中の求める人物像だといえるでしょう。

今週は、算数分野からの一問です。

ひとつの台の上に、点Aを中心とする一辺の長さ1cmの正八角形板と、一辺の長さ1cmの正六角形版が、図1のようにのっている装置を考えます。


正八角形板は台の固定されていて、台は壁に取り付けられています。正六角形板は図1の状態から1秒後に辺①と辺イが重なり、次の1秒後に辺③と辺ウが重 なり、この後も同じように動きます。
　このとき、次の問いに答えなさい。ただし、正六角形や正八角形とは辺の長さと角の大きさがすべて等しい多角形のことです。

（1）辺アと辺①が再び重なるのは、図1から何秒後ですか。
（2）正六角形板は図1から8秒間で中心Bの周りを何回転しますか。ただし、答えが整数にならないときは分数で答えなさい。

　今度はこの台全体も点Aを中心に32秒ごとに1回転するとします。例えば、図1から4秒後には装置は図2のようになっています。このとき、次の問いに答 えなさい。


（3）図1から36秒後に正六角形板のどの辺と正六角形板のどの辺が重なっていますか。
（4）図1から、初めて図3になるのは何秒後ですか。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（麻布中改題）

回転の意味を考えてみてください。正八角形に対する回転、台に対する回転、見ている私たちに対する回転をき ちんと理解することが大切です。

（１）六角形の辺の数6と、八角形の辺の数8の公倍数を考えます。つまり24辺分回転するともとにもどります。よって24秒後。　
（答え　24秒後）

（２）8秒間で、正六角形自身は　　　8÷6＝1と1/3　　回転します。そして、この8秒間で、正八角形のまわりを1周することで、さらに1回転するの で、答えは　2と1/3回転。　　　　　　（答え　2・1/3　回転）

（３）台が回転しても、正六角形と正八角形の関係はかわりません。
1秒後は②の辺が正八角形に接しています。2秒後は③が、そして6秒後に①の辺が正八角形に接しています。36÷6＝6・・・0　（36は6の倍数）　 　 であり、
正六角形の①の辺が、正八角形のいずれかの辺と重なっていることがわかります。
また、正六角形は8秒間で正八角形のまわりを一周するから、36÷8＝4・・・4　より、
4週と4秒後を考える。これより、正八角形の辺オが、正六角形の辺と重なっていることがわかります。　　　　　
（答え　正六角形の辺①と正八角形の辺オ）

４）図3では、正六角形の辺①と正八角形の辺オが重なっています。この状態は（3）の答え より、36秒後に起こることがまずわかります。また、（１）より、正六角形と、正八角形の重なる辺の組み合わせは、24秒後ごとに同じになることがわかるります。
したがって、
辺①と辺オの組み合わせは、
12秒後、36秒後、60秒後、84秒後、108秒後・・・　（ア）
に発生することがわかります。

また、台そのものについては、32秒で1回転しています。最初に図3の状態になるのは、4秒後である図2から180度回転すればよいので
4＋32÷2＝20秒後
です。その後は、32秒ごとに1回転するので
20秒後、52秒後、84秒後、116秒後・・・　　（イ）

に、同様の状態になることがわかります。
（ア）と（イ）より、84秒後に初めて図3の状態になることがわかります。　
（答え　84秒後）

大きな差を生んだ昨年度の問題です。

解く上での基本は、【ヒント】にも書いたとおり、
正六角形の回転数を、限られた正六角形と正八角形だけでなく、台も含めて考え、最終的に見ている私たちとの関係性
で回転数を答えなくてはいけません。

それを考えずに解けるのは（1）まででしょうか。
そして、同時にまわる正六角形と台の回転を分けて考えるなど、
図形をイメージする力だけでなく、論理的な数え上げ力も必要になってきます。
いずれにしても、公倍数の考え方を知らなくても出来る題材で、思考力の差をしっかりと測ることのできる良問でした。
（2）の解答の中にある、「さらに1回転するので」をすばやくイメージできたでしょうか。実際に考えてみてください。

また、上位校では本問のように、
「その場でルールを与えてゲームをしたり、ものを動かす」
といった問題が頻出しています。

この問題では、そもそも問題文（つまりルール）を理解できずに終わってしまう生徒も散見されます。理科と社会にも同じことが言えますが、問題文を理解する 国語読解力こそすべての基本だという学校側からの強いメッセージと問題意識の現われでしょう。
国語から逃げていては、このレベルでは全教科に渡って全く太刀打ちできません。

～ 今回の問題から導かれる出題校からのメッセージ～
・数式展開だけでな く、実際のものの動きを正確にイメージする力が重要
　近年、解法のパターン化が進み、問題を読んだだけで答えまでの数式の展開を一気に書き連ねる生徒が増えています。

しかし、数式は言語です。元になる現象のイメージを正確に理解して初めて、意味を持つのです。

途中式で出てくる数字が何を意味するのか、単位は何なのかきちんと把握できるイメージ力が求められています。麻布では、その場でルールを与えるゲーム形式 の問題や、図形の複雑な移動問題が頻出となっています。

・論理的な数え上げの能力
　
もれなく、ダブりなく数え上げる能力は、算数におけるもっとも基本的、かつ習得が難しい分野です。大学受験レベルと同様の問題の出題もめずらしくありま せん。思いつきで数え上げるのではなく、しっかりとした場合分け、数え上げの基本技術を身につけてください。その場で確実に正解にたどりつくというのは、 解答を理解することの何十倍も難しいことです。継続的な学習が必要な分野です。

--------------------------------------------------------------------------
ここに挙げた2つの力は、受験勉強最後の1年や数ヶ月で身につくことは絶対にありません。低学年のころから、良問に取り組み、過程を重視した指導を受け続け ることが必要です。ここを怠ると、高学年においてこれらの分野が非常に高い壁として感じられるようになり、「センスがない」という言葉で逃げざるをえなく なるのです。普段の学習の姿勢について考えさせられる問題です。

今週は、算数分野からの一問です。

0から9までの数字を1つずつ書いたカードがたくさんあります。このカードを組み合わせて整数を作り、下のように1から順に並べていきます。ある数まで作った ら、カードを全部で2989枚使いました。この数はいくつですか。また、このとき、１のカードは何枚使いましたか。（桜蔭中）

この問題を難しく感じる原因を考えましょう。1つの数字が1枚のカードで作られていれば答えは簡単ですよね？今回は、数とカードの枚数の当たり前の関係に着目してください。
　

1桁の数（1～9）：9個×1枚＝9枚
2桁の数（10～99）：90個×2枚＝180枚
3桁の数（100～999）：900個×3枚＝2700
この時点で 9＋180＋2700＝2889枚 つまり残りは100枚
ここから先は、4桁の数なので 100÷4＝25
25番目の4桁の数が答え。

解答を読んでいただければおわかりのとおり、かなり単純に見える問題ですが、桁数ごとに数え上げることで大幅に解答時間が短縮されます。
（桁ごとと言わず、すべての数を書き出せば解けそうに見えますし、実際解けるのですが、作業に多くの時間をとられ、他の問題にまで影響が出てしまいます。）

問われる力は大きく2つです。
・問題を複雑にしている原因を探ろうとする注意力
この問題を面倒なものにさせているのは、使うカードの数が桁数によって違っているということです。桁数ごとの場合わけがこの問題の突破口です。桁数ごとに数字を分けることは、意外と手間がかからず、1桁：9個、2桁：90個、3桁：900個ととてもきれいな数字になります。
・数え上げの基本能力
2桁の数10～99を99－10＝89個と数える。25番目の4桁の数を1000＋25＝1025とするなど、大人でも間違えることの多い数え上げの落とし穴が随所にちりばめられています。桜蔭中を受けるハイレベルの受験生でも、当日のプレッシャーのなかでこの単純な落とし穴に次々とはまってしまいます。

方針を立てるのに時間がかかり、4つの場合分けをしていくなかでも正確な数え上げ（計算）をこなす。正解者平均は5分での解答、不正解者の多くは20分程度数え上げに時間を費やし、結局間違いをするという結果でした。非常にレベルが高く、思考力により差のつく良問です。