学習塾ロジム　今週の1問by 学習塾ロジム

正しく「比べる」ことはできますか。

ある数Ｘを5回かけあわせた数を（Ｘ∧5）と表すことにします。つまり、

（Ｘ∧5）＝Ｘ×Ｘ×Ｘ×Ｘ×Ｘ

　となります。これについて、次の問いに答えなさい。

(1) （3∧15）＝（27∧ア）で、アにあてはまる数はいくつですか。

(2) （2∧10040）、（3∧8032）、（4∧6024）、（5∧4016）を小さい順に並べなさい。

同じ数を何千回もかける必要はありません。

(1) 5
(2) （5∧4016）、（2∧10040）、（4∧6024）、（3∧8032）

(1) まず、3を15回かけた数が、27をア回かけた数に等しいことから、3をかけ合わせて27ができることがわかります。ここで、3×3×3＝27ですから、（3∧15）の3を3個ずつセットにすれば27がかけ合わせられたことになります。15個の3を3個ずつセットにすると、15÷3＝5セットできることから、（3∧15）＝（27∧5）とわかります。

(2) まず、かけ合わされた個数があまりにも大きいことから、実際に計算してたしかめていくことは困難です。そこで、よく見てみると以下のとおり「かけ合わされた個数がどれも2008の倍数になっている」ことに気がつきます。

4016＝2008×2
6024＝2008×3
8032＝2008×4
10040＝2008×5

つまり、

4016＝2008×2→2個のセットが2008セットできる。
6024＝2008×3→3個のセットが2008セットできる。
8032＝2008×4→4個のセットが2008セットできる。
10040＝2008×5→5個のセットが2008セットできる。

これにより、

（2∧10040）＝（（2×2×2×2×2）∧2008）＝（32∧2008）
（3∧8032）＝（（3×3×3×3）∧2008）＝（81∧2008）
（4∧6024）＝（（4×4×4）∧2008）＝（64∧2008）
（5∧4016）＝（（5×5）∧2008）＝（25∧2008）

となり、比べることが容易になります。

2008の倍数であることに気づけるか否かで、所要時間が大きく変わる一問です。

-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています～

1.

2.
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー

大問における小設問は、いわば「ヒント」に他なりません。

生物は呼吸をします。



呼吸とは、空気中の酸素と体の中の栄養分を結びつけて、生きるために必要なエネルギーを取り出すことです。

この反応で使われた栄養は二酸化炭素と水になって体の外に放出されます。

呼吸に必要な栄養分(呼吸材料)には、ブドウ糖、脂肪、タンパク質があります。



呼吸材料の種類によって、反応するのに必要な酸素の割合がちがうので、

生物がどの呼吸材料を使って呼吸をしているのかは、

放出された二酸化炭素と吸収した酸素の体積比で調べることができます。この比を呼吸商といい、

以下の計算式で求めることができます。



　ブドウ糖、脂肪、タンパク質がそれぞれ呼吸材料として使われた場合の呼吸商の値を調べると、次のようになることが分かっています。





発芽直後のダイズ種子について呼吸の状態を調べるために、図のような装置を使って実験をしました。

［実験］

　図のように、赤い水滴が同じ位置に入った装置Ａ、Ｂを用意し、光を当てて３時間おき、ガラス管内の水滴の移動を調べました。なお、装置Ｂで用いる濃い水酸化ナトリウム水溶液は、空気中の二酸化炭素を吸収するはたらきがあります。

結果］

　装置Ａ：ガラス管内の水滴が、左の方向に４目盛り動いた。

　装置Ｂ：ガラス管内の水滴が、左の方向に20目盛り動いた。

このとき、実験に用いた発芽直後のダイズ種子の呼吸商の値を求めなさい。


　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（栄東　東大選抜）

装置Ａ、Ｂのガラス管内の水滴の移動は、どうして起こったのでしょうか。

0.8

　まず、それぞれの装置で水滴が動いた理由を考えます。

Ａ、Ｂどちらも水滴が左に動いていることから、フラスコ内の気体の量が減少していることは間違いありません。

発芽したばかりの種子は、激しく呼吸をすることから（これはこの問題の流れから容易に読み取れます）酸素が減少することはわかります。



ここで、装置Ａ、Ｂのちがいは水酸化ナトリウム水溶液の有無です。

　水酸化ナトリウム水溶液のあるＢでは、もともとフラスコ内に二酸化炭素はなく、さらに呼吸によって発生した二酸化炭素も吸収されてしまうため、実験の前後では酸素の量しか変化はありません。



　一方で、装置Ａでは呼吸に使われた酸素が減る一方で、発生した二酸化炭素の分気体の量は増えます。つまり、この差の分だけフラスコの体積が減ることになるのです。

　このことから考えれば、装置Ａ、Ｂでの水滴の動いた目盛りの差は、発生した（呼吸によって放出した）二酸化炭素の量であることがわかります。

　これより、以下のとおり呼吸商が求められます。

［以上、2008栄東・東大選抜より一部抜粋］

　さて、この問題がヒントなしですんなりと解答できたでしょうか。



このやや長いリード文と初めて聞く「呼吸商」という言葉から考えるとこれは難問の部類に入るでしょう。



正しい理論を持って、正答を導くにはかなりの時間を要した受験生が多かったはずです。

何よりも、装置Ａ、Ｂの違いが二酸化炭素に関係することはわかっても、答えをどのように導き出してよいかわからないためです。



　しかし、実際の入試問題ではこの設問の前に次のような設問が用意されています。

問　装置Ａ、Ｂのガラス管内の水滴の移動は、それぞれ何の体積が変化したことによるものですか。次のア～キから選び、記号で答えなさい。

　ア　呼吸により生じた二酸化酸素の体積

　イ　呼吸により吸収された酸素の体積

　ウ　呼吸により生じた二酸化炭素の体積と吸収された酸素の体積の差

　工　光合成により生じた酸素の体積

　オ　光合成により吸収された二酸化炭素の体積

　力　光合成により生じた酸素の体積と吸収された二酸化炭素の体積の差

　キ　呼吸および光合成により出入りした酸素の体積と二酸化炭素の体積の差

　まさに、今回「ヒント」として与えた内容です。

これにより、装置Ａ、Ｂの差異が明確になり、正答までの距離が大きく短縮されます。



ただ「初見問題を解くときは知らないからという理由だけであきらめないという姿勢が大切」というだけでなく、

具体的に身近なところからヒントを探る意識を持ちましょう。

-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています～

1.

2.
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー

調べるときは明らかに「闇雲＜きまり」であるという認識、意外に低いです。

１から８までの数が書いてあるカードがそれぞれ１枚ずつあります。この中から４枚のカードを取り出し、２けたの整数Ａ、Ｂを作ると、ＡとＢの最大公約数である２けたの整数Ｃも，残りのカードを使って作ることができました。ＡはＢよりも大きい数とします。ここで、Ｃのうちで最も大きい数は何ですか。また、最も小さい数は何ですか。

　
「条件から見当をつける→きまりをつくって調べる→確認（吟味）する」という、まさに整数問題の王道手順です。

最も大きい数　27　　最も小さい数　12

　２けたの整数Ａ、Ｂは２けたの整数Ｃの異なる倍数であることから、少なくともＡ＝Ｃ×３、Ｂ＝Ｃ×２でなければなりません。作ることのできる数のうち、最も大きい数が87であることから、Ｃは最大でも87÷３＝29となります。また、２けたであることからＣの最小値は当然12となります。よって、Ｃは 12～29までの値をとりうることがわかるので（見当がついたので）、最大については87から順に、最小については12から順に、整理してみます。
最も大きい数

同じカードを２度使えないことと、９、０が使えないことに注意しながら上の表のように順に調べていけば決して難しくありません。

近年、調べ上げることを極度に嫌う（面倒くさがる）子供が多く、
それは自分できまりを作ることなく「思いつき」や「闇雲に試す」という遠回りな作業をしていることが理由に他なりません。

　１つ１つ試していくのが面倒→思いついたのをとりあえずやってみる
　 →答えにたどり着かない（もしくはモレがあって正解に至らない）

という悪循環により、結果遠回りになっていることに気づいてほしいものです。

-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています～

1.

2.
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー

「何となく」が導く「うっかりミス」は「大きな過ち」です。

０、１、２、３の４つの数字を使った整数を１番目を０として、順に下のように並べます。

　　　　　０，１，２，３，１０,１１,１２，１３，２０，２１，２２，・・・

このとき、３４番目の数は何ですか。

正しい決まり（規則）を見つけてください。

201

０～３の４つの数字しか使えないわけですから、４進法で考えなければなりません。

つまり、簡単に言ってしまえば「３の次は４ではなく、位を変えなければならない」ということです。

これにしたがって数を並べてみると、３４番目の数は２０１であることがわかります。

　　０　　　１　　　２　　　３
　１０　　１１　　１２　　１３
　２０　　２１　　２２　　２３
　３０　　３１　　３２　　３３
１００　１０１　１０２　１０３
１１０　１１１　１１２　１１３
１２０　１２１　１２２　１２３
１３０　１３１　１３２　１３３
２００　２０１　・・・・・・・

　さて、実際「８１」と誤答を導いていないでしょうか？もちろん、この問題で使える数字に８はないわけですから正答ではありえません。

しかし、この問題の数の並びを見て、１の位に「０、１、２、３」の周期があると単純に思い込んでしまうと３４÷４＝８・・・２から、
９周期目の２番目、すなわち「８１」と答えてしまいやすいのです。

　さらに、そのような誤答を導いた場合、「あっ、何だ。そんなことか？！」や「うわっ、見落とした！」のように簡単なミスであったとすり返してしまう子供たちが多いことが一番の問題といえるでしょう。

また、きちんと４進法であることに気がつけば、この解説のように書き出すことなく式で処理をすることが可能です。

しかし、この場合にも「２０２」という誤答が散見されます。これは、最初の０を１番目とカウントしてしないことによるものですが、ここでも「うっかり１つずれてしまった」とミスとして終わらせてしまうのは、非常に悲しいことです。

　数多くの失敗を、その場限りではなく「次に同じ失敗がないように生かす」ことを意識してほしい、そんな一問です。

-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています～

1.

2.
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー

限界を考えることは、意外と難しいものです。

正方形の向かい合う辺の真ん中の点どうしを結ぶと、２つの合同な長方形に分割できます。

さらに、その長方形の長い方の辺の真ん中の点どうしを結ぶことで、右の図のように正方形を
作ることができます。そして、これを1回の「操作」と呼ぶことにします。
　下の図は、1辺が1cmの正方形について、この操作を３回繰り返したものです。これについ
て次の問いに答えなさい。

問1　
上の図で、3回までの操作を行ったときの最も小さな正方形（色つき部分）と、それ以外の部分の面積比を求めなさい。

問2　
1を順に半分にしていくと、1/2　、1/4　、1/8　、1/16　、1/32　、1/64　、…となります。このような数のならびで、1番目を　1/2　とし、順に番号をつけていきます。つまり　1/64　　は6番目となります。この数のならびで、100番目までの数の和と1はどちらが大きいですか。上の図を参考にして考え、大きい方を答えなさい。

図の各正方形の1辺に注目してみましょう。

問1　1：63
問2　1

問1　

最も小さな正方形（色つき部分）ともとの大きな正方形は、相似比が1：８の正方形です。よって、面積比は1：64になるので、もとの正方形から最も小さな正方形（色つき部分）を除いた分は63になります。

問2　

実際、100番目の数を求めようとするのは、かなり厳しいでしょう（10番目でさえも、　　ですから）。

100個もたしていくわけですから、1くらい平気で超えそうですが…。

さて、ここで図をもとに考えてみましょう。もとの1辺1cmの方形の下の辺を「操作」によってで

きた正方形ごとに見てみましょう。すると、順に、1/2、1/4、1/8、1/16、1/32、1/64、・・・・　となりますが、

どれだけ操作を繰り返して分割していっても、絶対にもとの正方形の1辺を超えることはありません。
よって、たとえ何番目まで足したとしても、1の方が大きいのです（極限の考えは除きます）。

まとめ
　「ひたすら足しまくるのだから、1くらい超えるだろう」という、常識（？）を覆す問題です。

高校数学でで極限を学べば、ある程度当たり前に感じることのできる内容ですが、小中学生には少々想像しがたいことでしょう。特に、問題のような図を与えず、ただ言葉や文章だけで出題したとすれば、おそらく全て（に限りなく近い数）の子供たちが1の方が小さいと答えるのではないでしょうか。

しかし、そんなイメージがわきにくいことも、図を用いてみるとあっけなく納得できるのです。図の力とは偉大ですね。
（どんなに1に近づこうとも、常にそのゴールまでの半分しか進めないというもどかしさがわかるはずです）
　この問題を通して、不思議だと思い、少しでも算数や数学に興味をもってもらえたら嬉しい、そんな一問です。

タイトル　2008-06-23

図を書いて試すのをためらったことはありませんか？

　下の図のような「あみだくじ」があります。これは、たとえば一番左のＡを選択した場合、図の太線をたどって左から４番目の位置に移動するものです。同じように、左から２番目のＢを選択すれば、左から３番目に移動することがわかります。このあみだくじについて、次の問いに答えなさい。

問１　Ａ～Ｉのうち、もとの位置よりも右に移るものはいくつありますか。
問２　このあみだくじをいくつか縦につなげて長いあみだくじを作ったところ、左から順にＡ、Ｂ、…、Ｉというように、はじめと同じ順番になりました。このとき、縦につなげたあみだくじは最も少なくていくつですか。

　ありません。

問１　５つ（Ａ、Ｂ、Ｃ、Ｅ、Ｇ）
問２　12個

　ＡＢＣＤＥＦＧＨＩは、このあみだくじによって下の図のようにＤＦＢＡＨＣＩＧＥと入れ替わります。
つまり、このあみだくじを１回通ることで、次の表のように整理できます。

つまり、左から１番目→４番目→１番目→…と、ＡとＤは２回ごとにもとにもどります。
同様に、左から２番目→３番目→６番目→２番目→…と、ＢとＤとＦは３回ごとにもとにもどります。
さらに、左から５番目→９番目→７番目→８番目→５番目→…と、
ＥとＧとＨとＩは４回ごとにもとにもどります。

以上より、２、３、４の最小公倍数である12回で、すべてもとにもどるのです。

まとめ
　誰もが一度は触れたことのあるであろう、あみだくじを題材にした問題です。それぞれの線が交差することで、一見複雑な動きをしていそうなあみだくじですが、要はただの入れ替え問題に他なりません。解説の表のとおり、どことどこが入れ替わるのかを整理すればさほど難しい問題ではないでしょう。

　しかし、実際にこの問題に取り組んだ子供たちは、多くが途中で諦めてしまいます（小学生に限らず、中学生でさえもです）。この理由は以下の２点が考えられます。

1）点や線が多く、面倒臭がって意欲が減退するであろうこと
2）図が大きいため、実際につなげて試すことが困難であろうこと

　過去にも、今週の一問で「調べ上げる」ことの重要性をお伝えしていますが、まさに本問も同様です。1）は学習姿勢に関係する避けがたい問題ではありますが、2）は工夫次第で容易に避けることのできる問題です。本問では、結局どこへ移動したのかさえ分かればよいので、下のように簡略した図で整理してみることが有効です（下の図では、例として１番目～３番目の移動先を図示しています）。このような工夫は、ぜひ経験から学び取って欲しいものです。

整数問題は、（整数という限定があるにもかかわらず）避けられがちです。

　０より大きい整数は、自然数とよばれます。そして、これらの自然数の多くは、連続したいくつかの自然数の和で表すことができます。たとえば、3＝1＋2、12＝3＋4＋5、100＝18＋19＋20＋21＋22などがその例です。これについて、次の問いに答えなさい。

(1) 98を連続した自然数の和で表すとどうなりますか。
(2) 1000以下の自然数の中で、連続したいくつかの自然数の和で表すことができないものはいくつありますか。

・奇数とはどのような自然数ですか？
・まったくイメージがわかなければ、とにかく調べることです。

(1) 11＋12＋13＋14＋15＋16＋17
(2) 10個

まず、偶数は2の倍数なので、必ず同じ自然数2つの和（□＋□）で表すことができます。
これに対し、奇数は偶数よりも1大きい数（□＋□＋1）ですから、
必ず□＋（□＋1）という2つの連続した自然数で表すことが可能です。
　
また、奇数の倍数（3の倍数、5の倍数、7の倍数、…）は、
等しい奇数個の自然数で表すことができるので、以下のとおり必ず連続した自然数で表すことが可能です。

3個　□＋□＋□→（□－1）＋□＋（□＋1）
５個　□＋□＋□＋□＋□→（□－2）＋（□－1）＋□＋（□＋1）＋（□＋2）
７個　□＋□＋□＋□＋□＋□＋□→（□－3）＋（□－2）＋（□－1）＋□＋（□＋1）＋（□＋2）＋（□＋3）

など…

　つまり、連続した自然数で表すことができない数は、偶数の中で奇数の倍数ではないものとわかります。
よって連続した自然数で表すことができない数は、素因数分解したときに奇数を含んではいけないわけですから唯一偶数の素数である2ばかりをかけあわせた数となります（1を除く）。

(1) 98は７の倍数なので、14＋14＋14＋14＋14＋14＋14→11＋12＋13＋14＋15＋16＋17と表されます。
(2) 1、2、4、8、16、32、64、128、256、512の10個です。

まとめ

整数問題は、難しいと思われがちですが、それは「調べる」作業を怠っている証拠です。
整数の問題は、特にことわりがなくても何か決まりがあるものです（そうでなければ問題になリません）。

この作業を面倒くさいと思うか、面白いと思うかは、大きな差であるといえるでしょう。

「勉強はつまらない」ではなく、
「何かの答えは自ら導き出してこそ意味がある」ことこそが勉強であることを知ってほしいですね。

「当選確実」、あなたは確実に処理できますか？

生徒数が480人の学校の生徒会で、４人の委員を決める選挙にＡ、Ｂ、Ｃ、Ｄ、Ｅ、Ｆ、Ｇの７人が立候補しました。開票数が410票になったところで１回目の中間集計を行うと、上位５名の得票数は下の表のとおりでした。この選挙で、無効票はなかったものとして、次の問いに答えなさい。

問１　第１回の中間集計で、当選確実となったのは誰ですか。すべて答えなさい。

問２　開票数が450票になったところで、２回目の中間集計を行ったところ、ＣとＤを除いた５名の得票数は下の表のとおりでした。このとき、Ｃが当選確実であるためには、最低何票獲得している必要がありますか。

数多く得票すれば当選確実ですが、そのラインとなるのは、むしろ「どれだけ少ない票で当選するか」です。

問１　ＡとＢ
問２　76票

問１　



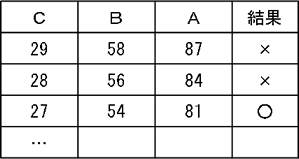
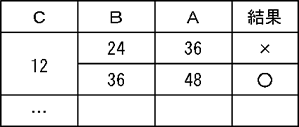
まず、当選確実となるライン（最低得票数）は、

「これ以上自分に票が入らないにもかかわらず、ギリギリ（最下位で）当選できる得票数」を表します。



たとえば、得票数の多いＡを考えてみます。

Ａを当選させないとすれば、Ｂ、Ｃ、Ｄ、ＥがＡの得票数をこえて101票ずつ獲得しなければなりません。

つまり４人で404票必要です。



しかし、これまでのＢ、Ｃ、Ｄ、Ｅの得票数と残りの票数を合わせても335票しかありませんから、これはありえません。



よって、Ａの当選は確実です。





次に、Ｂを考えてみます。

Ｂが当選確実であるならば、Ｂにこれ以上票が入らなくても当選できるわけですから、

現時点で得票数が多いＡも間違いなく当選確実になります。



よって、残り２人の枠を、ＣとＤとＥで争うことになります。ここで、Ｃ、Ｄ、Ｅ合わせて（86×3＝）258票あればＢを敗れますが、これまでのＣ、Ｄ、Ｅの得票数と残りの票数を合わせても250票にしかならないため、やはりＢも当選確実です。





さらに、Ｃを考えてみます。この場合、残り１人の枠を、ＤとＥで争うことになります。ここで、Ｄ、Ｅ合わせて（71×2＝）142票あればＣを敗れます。そして、これまでのＤ、Ｅの得票数と残りの票数を合わせると180票になるため、Ｃは当選確実とはいえません。

問２　

Ｃの当選確実を考えるのですから、ＡとＢは無条件で当選確実です。



ここで、ＡとＢ以外の２人の枠をＣ、Ｄ、Ｅの３人で争うわけですが、これまでのこの３人の獲得票数と残り票数は合わせて225票です。



よって、（225÷３＝）75票を越えれば、この3人の中での最下位はありえません。

よって、票以上獲得すれば、間違いなく当選できるのです。

まとめ

　この先、○○が△△票とったとすると…と、いろいろ考えすぎてしまいがちですが、

いかに必要な人物を見極めて、それらの得票数とまだ開票していない残りの票数を考えられるかが重要になります。



　当選確実について、解説にもあった次の２点が大切です。

当選確実となるラインは、「これ以上自分に票が入らないにもかかわらず、ギリギリ（最下位で）当選できる得票数」であること

誰かが当選確実であるならば、その人物よりも現時点で得票数が多い人物の間違いなく当選確実であること

　１つ１つ整理しながら、何度も何度も考えてみる価値のある問題です。

灘中より。問題文に明記されていない隠れた条件を使います。

2桁の整数が4つある。この4つの数のうちの2つの和と差を全部調べたら、和のうち最も大きいものは187で、最も小さいものは137であり、差のうちで最も大きいものは40で、最も小さいものは10である。4つの数のうち小さい方から2番目の数を答えよ。　（灘）

偶数と奇数をたすと奇数になります。

54つの2桁の整数を大きい順にＡ、Ｂ、Ｃ、Ｄとします。
問題文の条件は
Ａ+Ｂ＝187
Ｃ+Ｄ＝137
ＡｰＤ＝40
という式で表せます。

ここでＡとＢの和が187という奇数であることから、ＡとＢのいずれかが奇数であることがわかります。
よってＡとＢの差も奇数です。

同様に考えるとＣとＤの差も奇数です。
最小の差というのは、大きい順に並べたときのとなりとの差であるから（例えばＡｰＣが最小になることはない）4つの数のうちの2つの差の組み合わせで10となる候補はＢｰＣのみ。

よって、ＡとＢの差は11以上になるが、和が187でともに2桁の数という制約で考えると、Ａが99でＢが88という組み合わせしかない。
よって2番目に小さい数Ｃは88-10=78

答え78

いくつかの整数の和と差のヒントから元の数を考えるという問題です。

条件の与えられ方や題材（おもり、体重、テストの点）などは表面的に色々なバリエーションがありますが、ポイントは隠れた制限を見つけ出すことです。その主たるものが今回の偶奇と桁数の制限です。これらをつかってＡ+ＤとＢ+Ｃのどちらが大きいのかを判断したり、最大、最初の数を確定させたりします。

偶奇の性質の活用は、非常にシンプルなだけに思考から外れてしまいがちな難しい技術です。

「和や差から元の数を求める」という問題に出会ったときは、必ずチェックする項目として覚えておきたいものです。

「上手な足し算」を設計する力が問われます。

1，2，3，4，5の数字が書かれたカードが1枚ずつあります。これらのカードを使ってつくることのできる5桁の数すべての和を求めなさい。

全部で120通り。足し算をしていくには多すぎます。

5枚のカードを1回ずつ使うので、その並べ方は5×4×3×2×1＝120通りある。
これら120通りの5桁の数の各位を構成する数字に着目する。
120通りの一万の位には1,2,3,4,5が同じ回数ずつ使われている。つまり各数字24回ずつである。
千の位、百の位、十の位、一の位も同様。
つまり、すべての数の和は

（1×24+2×24+3×24+4×24+5×24）×10000+
（1×24+2×24+3×24+4×24+5×24）×1000 +
（1×24+2×24+3×24+4×24+5×24）×100+
（1×24+2×24+3×24+4×24+5×24）×10+
（1×24+2×24+3×24+4×24+5×24）
＝ （1×24+2×24+3×24+4×24+5×24）×11111=3999960
答え：3999960

効率的な数え上げを問う問題はその場での思考力を問わていると思われがちですが、
全く使った経験のない手法をその場で思いつくのはほとんど不可能です。

普段から、様々な問題に取り組み、模範解答で提示されている洗練された手法の仕組みをしっかりと確認していくことで蓄積されていくものです。

多くは、「数字を横ではなく縦に読む」つまり位ごとに整理していくという考えが根底にあるものです。答えがあっていただけで満足せず、様々な別解を探求する姿勢だけがこのような能力を高めることにつながります。