学習塾ロジム　今週の1問by 学習塾ロジム

H23年度　麻布中抜粋　【対象学年：5年生以上】



佐藤君と山田君がＡ地点からＢ地点に行くことになり、まず佐藤君がＡを出発し、次に午前10時に山田君が出発しました。それぞれ一定の速さで歩いていき、２人とも正午にＢにつく予定でした。しかし山田君は途中のＣ地点から自転車に乗り、進む速さを３倍にしたため、自転車に乗ってから４分後に佐藤君をＥ地点で追い越しました。そして佐藤君が正午にＢ地点に着いたときには、山田君はＢ地点からさらにＡＢ間と同じ距離にあるＤ地点まで進んでいました。

ＡＣの距離とＣＢの距離の比、ＣＥの距離とＥＢの距離の比をそれぞれ求めなさい。ただし、できるだけ簡単な整数の比で答えなさい。


















速さと比の問題では、時間・距離どちらかがそろっている部分を見つける意識が大切です。



























ＡＣ：ＣＢ=１：１　ＣＥ：ＥＢ=１：４

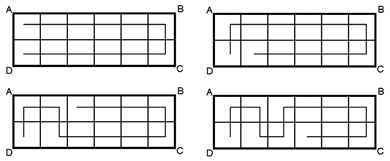
一見複雑な問題ですが、まずは分かる範囲で状況を線分図で表しましょう。



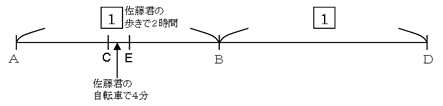
そして、ここから、距離やかかった時間が同じ部分を見つけます。速さと比の問題では、いかに距離や時間をそろえられるかがポイントです。距離の比を求める際には時間をそろえられないか、時間の比を求める際には距離をそろえられないか、と考えていきます。

この問題では、距離の比が問われているので、時間がそろっている部分がないかをさがします。

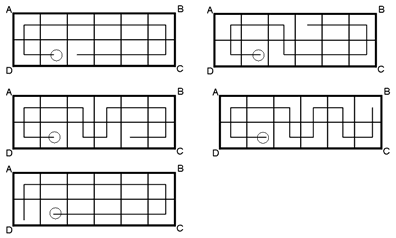
すると、山田君は本来12時にＢ地点に着く予定だったので、山田くんがC地点からＢ地点まで歩いたとしたときの時間と、C地点からD地点まで自転車で行ったときの時間が等しいことがわかります。山田君の歩く速さと自転車の速さは
１：３ですから、CB：BD=１：３　になります。（BDに注目すると□と○の関係がわかります・下図）

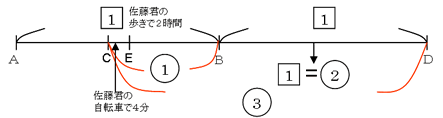
比をそろえると下図のようになります。よってＡC：CB=１：１です。

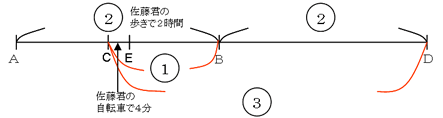
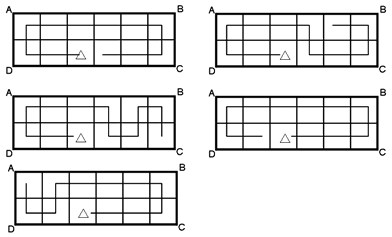
さて、次にCE：EBを求めます。これも距離の比を求める問題なので、時間の関係が分かる部分はないかと探っていきます。

今、ＡC：CB=１：１とわかったことで、佐藤君がAからBまで歩いて２時間でいくことから、CからBまでは１時間で行くことがわかります。また、佐藤君の　歩きの速さ：自転車の速さ=１：３　ですから

CE：CB=③（自転車の速さ）×４分：①（歩きの速さ）×60分=１：５　となります。
よってCE：EB=１：４　とわかります（下図）。　　

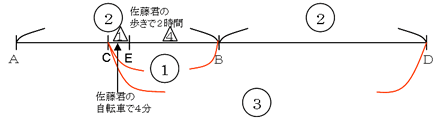
実際の入試でこういった問題が出題されると、できそうなのに、気づかないで焦ってしまうことが多いからこそ、「速さと比」の問題が合否を分けることもままあります。日頃から、「距離が問われているから、時間が同じところをさがそう」といった「～を求めたいのだから、どこがわかればいい」という逆算的な考えで論理的に考えるようにしたいですね。

小学生が作った平均に関する良問　【対象学年：5年生以上】



太郎くんは2010年中に何回かテストを受け、その平均点は70点でした。2011年になって最初のテストで94点をとったので、2010年からのこれまでの平均点が74点になりました。

太郎君は2010年中に何回テストを受けましたか。
















実際値の合計　÷　その数字の個数　＝　平均値　
ですから
平均値　×　その数字の個数　＝　実際値の合計



















5回


確か岐阜県か岐阜市で過去に行った算額コンクールで小学生が作った問題です。シンプルでとてもいい問題だと思います。

インターネットで出典を再度探したのですが見つからなかったので記憶をたどって問題を再現してみました。（もしかしたら設定はオリジナルとは違うかもしれません。）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
2010年中に受けたテストの平均点が70点であることを図示すると下のようになります。


2010年中の合計点　を　？回で割ると　70点になるわけですから、言い換えれば、

70点　を　？回　足し合わせると　2010年中の合計点　になります。
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
2011年に1回受けたテストの結果を加えた平均点が74点であることを図示すると下のようになります。



これまでの合計点を　（？+1）回で割ると　74点になるわけですから、言い換えれば、

74点を　（？+1）回　足し合わせると　2011年も含めたこれまでの合計点　になります。
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
ここで次のような式をつくることができます。

70点×？回　＝　2010年の合計点
74点×（？+1）回＝2011年までの合計点＝2010年の合計点+94点

したがって、

70点×？回　＝　74点×（？+1）回 － 94点
70×？　＝　74×？+ 74 － 94
？＝ 5

となり2010年中は5回テストを受けていたことが分かります。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
おそらくこの問題を作った小学生は平均の考えた方を完璧に理解できていると思います。自分で問題を作るというのは、その分野を理解するための最良・最高の方法です。もちろん手間はかかりますが、その効果は絶大です。積極的に作問に挑戦してみてください。

いい問題ができたら是非ロジムで紹介しますので教えてください。
--------------------------------------------------------------------------------
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー

サイコロの塗りわけ【対象学5年生以上】

1から6までの数字がかかれたサイコロがあります。6色の絵の具を使い、隣り合う面が違う色になるように塗り分けます。全部で何通りの塗り方がありますか。6色すべてを使う必要はありません。

使う絵の具の種類によって場合わけしていきます。

4080通り

(i)3色で塗り分ける場合
1と6,2と5,3と4を同じ色にします。
1と6の塗り方は6通り,2と5の塗り方は5通り,3と4の塗り方は4通りなので6×5×4＝120通り

(ii)4色で塗り分ける場合
まず、1と6,2と5,3と4のうち2組を選んで2色使います。そして残りの2面に使っていない4色のうちから1色ずつつかいます。
選ばれた2組をAとB,残りの2面をCとDとすると塗り方は6×5×4×3＝360通りです。
AとBの選び方は,1と6,2と5,3と4の3組から2組選ぶので3通りあります。よって4色で塗り分けるのは360×3=1080通り

(iii)5色で塗り分ける場合
まず、1と6,2と5,3と4のうち1組を選んで1色使います。そして残りの4面を4色で塗り分けます。
選ばれた1組をA,残りの4面をB,C,D,Eとすると塗り方は6×5×4×3×2=720通りです。
Aの選び方は,1と6,2と5,3と4の3組から1組選ぶので3通りあります。よって5色で塗り分けるのは720×3=2160通り

(iv)6色で塗り分ける場合
6×5×4×3×2×1=720通り

以上より合計4080通り

場合の数に関する基本事項が全て含まれている良問です。
和の法則,積の法則,そして「まず枠組みのパターンを決定して,塗り分けを考える」という手順です。
解答の(i)～(iii)にあるように,まず「どことどこを同じ色にするか」ということが先決です。下の図のような地図の塗り分け問題は見たことがあるのではないでしょうか。

この場合も,まずどことどこを同じ色にするかを決定します。4色で塗り分けるなら、AとEを同じにするかBとCを同じにするかCとEを同じにするかのパターンがありますね。

さらに場合の数の応用として,「回転させて同じになるものは1通りと考える」というものがあります。
本問をサイコロではなく,数字の書いていない立方体と考えて「6色すべてを使って塗り分けるのは何通りか。」を考えてみてください。

--------------------------------------------------------------------------------

参考書選びの参考にご利用ください。

ロジム2階参考書コーナー

小問の誘導と対称性の利用(３年生以上)

1辺１ｃｍのサイコロを右図の１辺1ｃｍの正方形が１２個ならべられた台紙(下図)のうえを
すべて１回ずつ通るように移動させます。

(１)図の左下(頂点Dをもつ正方形)から始めた場合、転がし方は何通りありますか。
(２)スタートする正方形を自由に選ぶとき、何通りの転がし方がありますか。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　2011開智中先端A入試改題

(１)は自分なりの基準を作って実際にやってみましょう。
(２)(１)の結果を利用できる方法はないか考えてみましょう。



























(１)6通り
(2)64通り

(1)何回か実際に転がしてみましょう。そうすると、横に2マス以上転がしたあと、段をかえてしまうと空白ができてしまうことに気付きます(たとえば下図)。

よって段を変える前に、それより左側のマスをすべて通っておく必要があるため、どこのポイントで横にまっすぐ進むかを基準にルートをえらべばよいことになります。そうすると、以下の6通りの通り方が考えられます。

(２)スタートの正方形をどこでも選んでよいので、一見とても大変な問題に見えるかもしれません。しかし、４角はひっくり返したり、裏返したりすれば、(１)とまったく同じ状況になる(下図a
☓部分は結局６通りずつである)とわかれば、処理の手間がかなり減ります。

同様に、上図の◯の部分、△の部分も、すべて同じ数ずつ通り方があることになります。

つまり◯からスタートする場合と△からスタートする場合を1つずつ調べてそれを４倍すればいいわけです。

(ⅰ)◯からスタートする場合

最初に上に進んでしまうと、(1)のときと同様、通れないマスができてしまいますから、最初に◯より左側、または右側をすべてうめておかなければいけません。
どちらかをうめたあとは(１)と同様、横にまっすぐ進む前に、その後ろ側をすべてうめておかなければなりませんね。よって最初に左側をうめる場合が４通り、右側をうめる場合が１通りで、合わせて5通りの通り道があります。

(ⅱ)△からスタートする場合も(ⅰ)の場合と同様のルールで数えましょう。

この場合、最初に左側に行く場合に3通り、右側に行く場合に2通りの合わせて5通りの通り道があります。

以上より、図aの☓部分からのスタートが６通り、◯部分・△部分からのスタートがそれぞれ5通りあるので、全部で

(6＋５＋5)×４＝64　通り　の通り道があることになります。

このように、複雑に見える問題でも、まず手を動かしてルールや基準を発見すれば、正確に数えることができます。そしてそれをうまく使って、より複雑な問題を解けないか、と考える姿勢を持ちましょう。対象学年は３年生以上としましたが、特別な知識も不要な問題という点では、もっと低学年の人でもできる問題ですね。

--------------------------------------------------------------------------------

参考書選びの参考にご利用ください。

ロジム2階参考書コーナー

数列の利用【対象学年：４年生以上】

下の数列は
１，１，２，３，５，８，１３，２１，３４，・・・
「前の２つの数を加えると次の数になる」という数列です。


この性質に似た性質がかくれている問題が直線の本数とその交点の数です。
直線に対してできるだけ多くの交点を作った場合

と交点が増えていきます。

（１）７本目の直線をひいたとき６本目のときより何個交点は増えますか。
（２）直線が８本のときの交点の数は何個ありますか。
（３）100本目の直線をひいたとき99本目のときより何個交点は増えましたか。

　直線の本数と交点の数、そして「前の２つの数を加えると次の数になる」ことを意識して考える。



























(1)６個
(2)28個
(3)99個

(1)数本の直線に対して新しく１本の直線を引いた場合、その数本の直線の1本につき１つの交点が新しくできます。
例えば、３本の直線に対して新しく１本の直線を引いた場合は下の図のようになります。

３本の線に対して、１本の直線を引くことにより、その３本に新しく交点が１つずつできます。よって、６本の線に対して７本目の直線を引くと新しく６個の交点が増えることになります。

手前の本数の数と交点の数を足すと次の交点の合計になっていることがわかります。

(3)上の表より新しくできる交点の数は、１つ手前の直線の本数と等しくなっていることがわかります。よって、100本目の直線の交点はそれまでの99本の直線と交点をつくるので99個になります。

--------------------------------------------------------------------------------

参考書選びの参考にご利用ください。

ロジム2階参考書コーナー

規則性の発見と誘導の利用　【対象学年：4年生以上】



１、２、３、・・・と番号がかいてあるカードが、上から番号の小さい順に重ねてあります。『一番上のカードを捨てて、その次に一番上になったカードを残りのカードの一番下に入れる』という操作を繰り返すとする。次の問いに答えなさい。

（１）カードの枚数が32枚の時、最後まで残るカードの番号はいくつですか。

（２）カードの枚数が1100枚の時、最後まで残るカードの番号はいくつですか。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
　　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（慶応義塾湘南藤沢中・改題）

（２）に関しては、（１）をうまく利用できないかどうか考えてみましょう。



























（1）　３２　　（２）152

（１）操作の手順にしたがってやってみましょう。
　　（1.2.3.4.・・・29.30.31.32）と並んでいる中で、１が取られて、２がうしろに、３が取られて４がうしろに・・・となるので、カードが一周したときを考えると、偶数が１６枚残ります。

　　次に、（2.4.6.8.・・・26.28.30.32）と並んでいる中から、２が取られて４がうしろに、６が取られて８がうしろに・・・となるので、再度カードが一周したとき　　を考えると、 ４の倍数が８枚残ります。

　　よってこの時点で（4.8.12.16.20.24.28.32）が残っています。
　　ですから、同様の操作を繰り返すと（8.16.24.32）→（16.32）→32となり、最後に32が残りますね。

（２）（1）より、32枚の時には、32が残ります。
　　では、64枚（32×2）のときを考えてみましょう。64枚のカードをこの操作で一周させたときには（2.4.6.・・・60.62.64）の３２枚のカードが残ります。
　　ここで、32枚のカードがある時には、その最後の1枚が残るわけですから、64が残る、すなわち64枚のカードがある時には64が最後に残ることにな　　ります。

　　同様に、128枚、256枚、512枚、1024枚の時にも、それぞれその最後の数字のカードが残ることがわかります。
　　
　　よって1100枚から76枚取り除き、残りが1024枚になったときに、最後にある数字が求める答えとなります。
　　76枚取り除いたときに、いちばんうしろに来る数字は76×2＝152ですから、152が最後に残る数字となります。

　　　もちろん、この問題を書き出しによって求めることも可能ですが、（1）で少ない数での実験をやらせた後に、法則を発見させ、（２）でそれを使って考えさせるという問題は数多く出てきます。何とか（1）をうまく使えるような法則がないかどうか、考えてみることが大切です。

--------------------------------------------------------------------------------

参考書選びの参考にご利用ください。

ロジム2階参考書コーナー

倍数に注目しよう　【対象学年：5年生以上】



345は３で割り切れます。

1473は３で割り切れます。

857421は３で割り切れます。



このとき、

345の各位の和は３＋４＋５＝12

1473の各位の和は１＋４＋７＋３＝15

857421の各位の和は８＋５＋７＋４＋２＋１＝27

となり、それぞれ３の倍数となっています。



次の問いに答えなさい。



(１)下記はなぜ各位の和が３の倍数であれば３で割り切れるのかを説明した文章です。

　　空欄に入る数をいれなさい。



1473を、各位に分けて式で表すと、

１×1000　＋　４×100　＋　７×10　＋　３

となります。

次に、式をわけると次のようになります。
１×［ ア ］＋１　＋　４×［ イ ］＋４　＋　７×［ ウ ］＋７　＋　３

とすると、各位の数を１個ずつ集めることが出来ます。
１×［ ア ］　＋　４×［ イ ］　＋　７×［ ウ ］　＋　１＋４＋７＋３

これを、それぞれ３で割れば下の式のように
（１×［ エ ］　＋　４×［ オ ］　＋　７［ カ ］　＋　［ キ ］）×［ ク ］
とまとめることが出来ます。
よって、各位の和が３の倍数であれば３の倍数といえます。

同じ考え方で［ ケ ］の倍数も説明できます。

７×５は７が５つと考えると、７×４＋７と表せます。



























ア　999
イ　99
ウ　9
エ　333
オ　33
カ　3
キ　5
ク　3
ケ　9







１×1000　＋　４×100　＋　７×10　＋　３をそれぞれ、
１×999＋１　と　４×99＋４　と　７×９＋７　と　３　
にわけることがポイントです。
こうすることで、１×999と４×99と７×9は３
そして、残った１＋４＋７＋３(各位の和)が３の倍数であれば全ての数が３で割り切れるといえますね。

ケについても１×999と４×99と７×9は９の倍数といえるので、残っている各位の和が９の倍数であれば、９で割り切れるといえます。

--------------------------------------------------------------------------------

参考書選びの参考にご利用ください。

ロジム2階参考書コーナー

　【超有名問題】囚人のジレンマ【対象学年：5年生以上】

AとBは共同で犯罪を行ったとされ逮捕されました。2人は別室に隔離されました。警官はこの2人に自白させるために、彼らの牢屋をそれぞれ順に訪れ、以下の取引を持ちかけました。

「もし、おまえらが2人とも黙秘したら、2人とも懲役2年だ。だが、共犯者が黙秘していても、おまえだけが自白したらおまえだけは刑を1年に減刑してやろう。ただし、共犯者の方は懲役15年だ。逆に共犯者だけが自白し、おまえが黙秘したら共犯者は刑が1年になる。ただし、おまえの方は懲役15年だ。おまえらが2人とも自白したら、2人とも懲役10年だ。」

つまり、
・どちらか一方が自白すれば、自分の刑は1年になり、黙っていた方は15年になる。
・両方が自白すると、2人とも懲役は10年
・両方が黙っていると、2人とも懲役2年
という条件（ルール）が提示されました。

（なお、2人は双方に同じ条件が提示されている事を知っているものとする。また、彼らは2人は別室に隔離されていて、2人の間で強制力のある合意を形成できないとする。）

ここで、Aは共犯者のBを裏切って自白すべきか、それとも黙秘すべきか判断しなさい。




















Bが黙秘した場合、裏切って自白した場合、それぞれに分けて、Aの行動を考えます。



















裏切って自白すべき




Bが裏切って自白した場合（上表：赤の部分）　
⇒　Aは自分が黙秘すると15年懲役、自白すると10年懲役。したがって、裏切って自白したほうが懲役年数は少ない。

Bが黙秘した場合　（上表：青の部分）
⇒　Aは自分が黙秘すると2年懲役、自白すると1年懲役。したがって、裏切って自白したほうが懲役年数は少ない。

Bが自白しようが、黙秘しようが、Aにとって懲役年数が少なくなるのは、裏切って自白した場合となる。したがって、Aにとっての最適戦略は「裏切って自白」となる。

（有名な「囚人のジレンマ」です。この問題は一回完結タイプであり、判断が繰り返しになる（繰り返しの回数を知っている）と違った判断が得られます。これもいつか「今週の1問」で取り上げます。）

ゲーム理論という分野の有名初歩問題です。小学生にとってもおなじみの思考パターンですね。「起きる事象を場合分けし、そのそれぞれについて検討する」。論理的な場合分けの力と、丹念に考えを積み上げる力は訓練ですぐに身につきます。

--------------------------------------------------------------------------------
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー

　範囲を意識する問題 H14市川中学校第1回より【対象学年：5年生以上】





長方形の土地ABCDの周の上を歩きながらヒマワリとアサガオの種を植えます。Aから時計まわりに３m歩くごとに、ヒマワリの種を全部で９粒植えました。また、Aから反時計まわりに２m歩くごとに、アサガオの種を１粒ずつ全部で20粒植えました。どちらの種も、ひとまわりしないうちになくなりました。何日かたってみると、Cからはヒマワリとアサガオの両方が生えていました。この土地の周の長さは何mですか。

図にヒマワリとアサガオを書いていってみると何かに気づけるかも。
やっぱり地道に手を動かしてみることが大切です。

48m

３ｍずつ植えて、１周の半分であるC地点に植える。２ｍずつ植えて１周の半分であるC地点に植える。ということは、C地点はA地点から３ｍと２ｍの公倍数分、離れているということになります。

また、A地点からヒマワリを９粒植えたとき３×９＝27(ｍ)分植えたことになります。もし、A地点からC地点までが27ｍ以上離れていたらC地点に種が植えられません。よって、C地点までは３×９＝27(ｍ)以下となります。

次にアサガオを考えてみましょう。

すると、A地点から２×20＝40(ｍ)歩いても1周しないことが分かります。よって、1周は40ｍ以上になります。A地点からC地点までは1周の半分になるので40÷２＝20(ｍ)以上でなければいけません。
以上の範囲を考えると、A地点からC地点までは、20ｍ以上27ｍ以下であり、なおかつ３ｍと２ｍの公倍数であることになります。その条件を満たす数字は、24ｍのみとなります。半周が24ｍとなるので、1周は24×２＝48(ｍ)となります。



複雑に感じることも、実際に図を書いて手を動かすことで範囲が意識できます。

解説を読んだあとに図を書き手を動かしてみると単純だったことに改めて気づけるはず。

-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています～

1.

2.
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー

　有名事実を確認しよう【対象学年：5年生以上】





円Oの周上を毎秒12度動く点Ｐと毎秒6度動く点Ｑがあります。点Aを同時に出発し、矢印の方向に動くとき、三角形APQがはじめて直角三角形になるのは何秒後か。

ありません。

三角形APQの辺のうち1つがOを通る、すなわち直径となったときに三角形APQは直角三角形になる。ＰとＱが180度離れるのは10秒後。このとき初めて三角形APQが直角三角形になる。

答え：10秒後

様々なテキストで、「三角形APQの辺のうち1つがOを通る、すなわち直径となったときに三角形APQは直角三角形になる」と解説されることがある本問ですが、なぜこのとき三角形が直角三角形になるのかを確認しておくことが大切です。

下の図のようにAOを通る補助線を引きます。

OA=OQなので三角形OQAは二等辺三角形となります。よって○は同じ角度となります。三角形OAPについても同様に□が同じ角度になります。それぞれの三角形の外角を考えると、○○＋□□が180度となっています。よって○+□は90度となります。三角形APQの内角のうち角PAQは○+□なので、三角形APQは直角三角形となります。

この考え方は下の図のようにPQが直径となっていなくても成り立ちます。

この図でわかるとおり、角PAQは中心角POQの半分の角度になっています。角PAQは中心角POQに対して、円周角とよばれ、常に中心角の半分の大きさになっています。円周角の定理と呼ばれるもので中学範囲ですが、全く同じ考え方で解く問題は頻出となっています。

-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています～

1.

2.
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー