極端な場合を考えて見通しをよくします。 2007-10-22
極端な場合を考えて見通しをよくします。

箱の中に3と書かれたカードと5と書かれたカードがそれぞれたくさん入っています。この箱からカードを何枚か取り出し、書いてある数の合計を調べます。たとえば、合計9になるのは3のカードが3枚取り出される場合のみの1通りです。このとき合計2003になる取り出し方は何通りありますか。

ノーヒントです。

なるべくたくさんの3のカードをつかって2003を表すことにする。
すると2003÷3=667余り2より、3のみで2003を作ることは不可能です。そこで余り2に着目し、
2003=3×666+5×1
より666枚の3のカードと、1枚の5のカードで作る組み合わせが出来ることを確認する。
ここで、合計の2003を変えずにカードの組み合わせを変えていく。
つまり、合計を変えないようにしながら、3のカードを減らし、5のカードを増やす。
(なぜなら3のカード666枚は最多の場合だから)
合計を変えないためには減らした3のカードの合計と増やした5のカードの合計が同じになるようにしなくてはいけない。
つまり3と5の最小公倍数に着目して、3のカードを5枚分合計15減らし、
5のカードを3枚分合計15増やすという作業によって、組み合わせを変えていけばよい。
3のカード666枚を5枚ずつ減らしていく作業は666÷5=133余り1より133回実施することができる。
よって組み合わせは最初に見つけたものと合わせて134通り考えられる。
答え:134通り

様々な組み合わせを考える問題はまず極端な場合を考えて、
どれくらいの範囲にあるのか、概算をすると見通しがよくなります。
つるかめ算と同じ考え方です。本問はなるべく多くの5のカードを使う場合からスタートしても解くことができます。
また、次に取組むことになる「和を一定に保つ」ための作業は、いろいろな形に姿を変え出題されます。
当然、増やした分を減らす、掛けた分を割るという還元作業をすればよいのですが、そう単純にはいきません。
本問は減らすときには3が単位となり、増やすときには5が単位となります。
このように、還元するときに単位が変わる
(水を捨てるときと入れるときの単位時間当たりの水量が違うなど)のが常套なので、
両者を丁寧にそろえる作業から手をつけていきましょう。
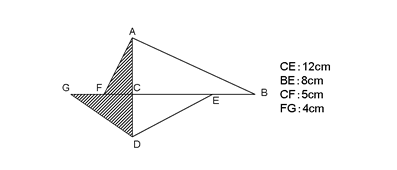
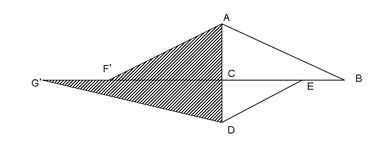
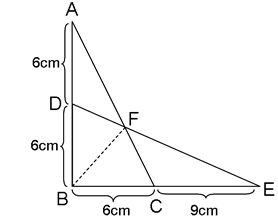

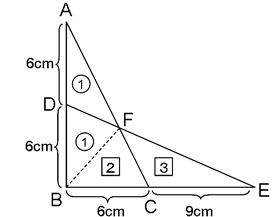
 は=11.25なのでもとめる三角形ABCと三角形DBFの面積の比は
は=11.25なのでもとめる三角形ABCと三角形DBFの面積の比は