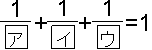学習塾ロジム　今週の1問by 学習塾ロジム

筑波大付属中より。問題文を読む姿勢が問われます。

算数のテストの得点を調べたら、0点の人は1人もいませんでした。また、田中さんの得点から中村さんの得点をひいた差が、ちょうど山本さんの得点と同じになりました。次のうち、正しいものはどれでしょう。

（ア）田中さんの得点は、中村さんの得点と山本さんの得点の和よりも多い。
（イ）田中さんの得点と山本さんの得点の和がちょうど中村さんの得点に等しい。
（ウ）中村さんと山本さんの得点はどちらも田中さんの得点より少ない。
（エ）田中さんの得点と中村さんの得点の和がちょうど山本さんの得点に等しい。

(筑波大付属中）

「差」を扱う問題の定石手法が突破口です。

問題文の
「田中さんの得点から中村さんの得点をひいた差がちょうど山本さんの得点と同じになりました。」
を線分図で表すと下記の通りとなる。

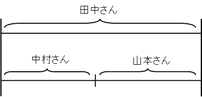
よって
ア：田中さんの得点と中村さん、山本さんの得点の和は等しいので誤り
イ：田中さんの得点は一番高いので明らかに誤り
エ：田中さんの得点は一番高いので明らかに誤り

答え：ウ

不等式など、関係性を数式処理によって表して処理しようとすると複雑になり、
時間もかかってしまいます。

問題文の「差」という表現に着目し、線分図によって整理するという定石手法によって問題の整理が一気に進みます。

旅人算などもそうですが、与えられた情報を見やすい形に整理して、
より多くの情報を引き出すという姿勢をもっていることが必要となる問題でした。

～今回の問題より導かれる出題校からのメッセージ～
問題文の条件の図式化が大切

線分図をはじめとして小学生では「～図」に整理するという手法を数多く学びます。

方程式にとってかわられるという理由で避けてしまう指導者、生徒も多いのですが、
この図式化によって学べることは、方程式によって学べることとは異質のものです。

式の処理によってだけでなく、図にして幾何学的に考える作業というのは高度な数学の能力として必要となるものであり、
なにより数の性質を多面的に捉えることになる魅力的な手法です。

現実問題として、昨今の入試問題では、
方程式で処理した場合時間がかかりすぎてしまう仕掛けがされることも多くなっています。

小学生ならではの様々なものの捉え方を楽しむ姿勢が必要です。
洗練された図式化により一気に解ける。図式化の価値と面白さを教えてくれる良問でした。

灘中より。無粋な手法の中にも答えがあります。

下の2つの図は、各面に1から6までの数が書かれた立方体の展開図である。それぞれの立方体の1つの頂点に集まる3つの面に書かれた数の和を考える。この和のうち最大のものは（図1）では15、（図2）ではいくつか。
　　　　　　　　　

(灘中）

そもそも頂点の数は・・・。

組み立てた状態を考えると下の図のようになります。

頂点は8こなので、8つの頂点についてすべて調べてみます。
すると
4＋2＋3＝9、
4＋2＋6＝12、
4＋1＋3＝8、
4＋6＋1＝11、
5＋1＋3＝9、
5＋3＋2＝10、
5＋2＋6＝13、
5＋6＋1＝12
となり、最大のものは13。

答え：13

「最大」を生み出すメカニズムについて検討する姿勢はとても大切です。

しかし、場合の数など組み合わせについて考える問題においては、
そもそも検討すべきパターンがいくつぐらいあるのかについて概算してみる姿勢が大切です。

本問では実は8つの頂点についてしらみつぶしに調べればすぐに終わります。

～今回の問題より導かれる出題校からのメッセージ～
作業量の見通しを常に検討する姿勢が大切

「しらみつぶし」は、上位の生徒にとって、そして指導者にとってあまり洗練されたものではありません。

しかし、状況に応じて「最善」である場合もあるのです。

例えばさいころ問題では2個のさいころであれば36通りの組み合わせしかありませんから、
すべて調べてもたいした時間はかからない上に、確実です。

反対に4個ですと、1296通りですから、何か法則を見つけなければ太刀打ちできません。

解法を決めてかからず、解いている最中でも常に別の道筋を検討する姿勢は、
本校が生徒に期待する学問に対する姿勢に他ならないといえます。

灘中より。割り算の筆算ができますか？

整数（A）を整数（B）で割ると、商が32で余りが10であった。さらに割り算をつづけて小数第3位まで求めると商は32.322となり、余りが出た。（A）（B）に入る数を求めなさい。

(灘中）

「割り算を続ける」という作業を筆算で確認してみてください。

商が32、余りが10の状態からさらに割り算を続けるというのは、
余りの10を整数（B）で割るということです。

その商が32に続く小数部分となります。

つまり
10÷B＝0.322・・・である。
よってB＝31.05・・・・からB＝31
ゆえにA＝32×31＋10＝1002

答え：A：1002　　B：31

計算や筆算の仕組みを理解し、きちんとイメージできるかどうかが問われています。

50分で15問ですから、本問に割くことのできる時間はだいたい2分程度です。

普段から定石問題についても深い考察をしていくことが大切です。

本問は割り算の筆算の手順についてイメージできればとても簡単な問題です。

「割り算を続ける」とは、「余りを割り続ける」という作業なのです。

～今回の問題より導かれる出題校からのメッセージ～
計算技術の仕組みと意味の理解が大切

灘中ではよく出題されるポイントとして、 筆算や各種の法則などを
使うことには慣れていてもその仕組みや意味をきちんと説明すること
が難しい知識を必要とされるものがあります。

かつては壮大な虫食い算などが主流でしたが、最近は本問のような
計算の経過を文章で与えるという形式が好まれています。

本問も普通の割り算を文章化しただけなのですが、とたんに混乱して
しまう生徒も少なくありません。

一度低学年にするような形で説明する機会を持たせると、高学年
でも様々な計算技術の中に気付きを得られると思います。

それらの気付きなしでは、本校の1日目を高得点で乗り切ることは
不可能です。当たり前の知識に関しても表面的な理解に留まらず、
きちんと検討する。　1日目の問題はそういった付け焼刃では身に
付かない勉強への基本姿勢を測定する問題だといえるでしょう。 。

駒場東邦中より。複雑な立体切断を基本定理に落とし込みます。

下の図のように1辺の長さ2ｃｍの立方体を4個はり合わせてできた立体を考えます。この立体を3つの頂点Ａ、Ｂ、Ｃを通る平面で切断しました。

（１） 上の図に切り口の図形を書き入れなさい。

（２）（３）省略

(駒場東邦中)

切り口のラインの中で、明らかなものからひとつずつ描いて行きましょう。

切断面は図のとおり

立体図形を平面で切断したときにできる 断面の切り口を求める問題では
基本のルールをしっかりと追っていくことが重要になります。

（基本ルール１）
切断面は必ず切断するように指定された点を通る
当たり前のように思えますが、一番大事なルールです。
今回の場合、これでまず頂点Aと頂点Bを結ぶ直線が結べます。

また、

（基本ルール２）
切断面は必ず連続している
も一見当然のように見えますが大切なルールです。

（基本ルール３）
向かい合う平行な平面の上を通る切り口は平行である
このルール２を使うと、ルール１と合わせて頂点Cから線分ABと平行につながる
切り口を描くことができます。

（基本ルール４）
切断する平面上の各点を結ぶ線上に、切断される立体の外壁が重なれば
そこは切り口である

ここまでくると、すこし立体的な想像力が必要となってきます。
ただ、最初の３つのルールに従って条件整理ができていれば
作業はずっと間楽になっているはずです。

ここで三角形ABCを考えてみると頂点Aと頂点Bから
斜めにのびる線分が引けます。
ここさえ書くことができれば残りの線は すべて最初の３つのルールから描くことができます。

～今回の問題より導かれる出題校からのメッセージ～
想像力の不足は論理の積み重ねで補うことが大切

算数の図形問題、とくに立体図形の問題はひらめきや立体的なイメージ力 が大切だと思われがちです。

しかし、今回の問題のように基本のルールをしっかりと守って きちんと条件整理をすることで 一見トリッキーに見える問題でもずっと簡単に解くことができます。

どんな算数の問題でも大事なのは基本的なルール。
一見難しそうに思える問題でもしっかりと条件を整理していけば 簡単な基本の組み合わせに分割できることを理解しましょう。

灘中より。非常に短い問題文を整理する国語力が問われます。

ある5桁の整数があります。この整数には、数字0がA個、数字1がB個、数字2がC個、数字3がD個、数字4がE個使われていて、これ以外の数字は使われていません。また、この5桁の整数は一万の位から順にABCDEとなっています。ABCDEの中には同じ数字があってもよく、BCDEは0であってもよいものとします。この5桁の整数を求めてください。

(灘中）

紛らわしいかたちで与えられている2つの条件を整理しましょう。

A、B、C、D、Eは、それぞれ5桁の整数の中で、0、1、2、3、4の数字が使われている個数ですから、
A＋B＋C＋D＋E=5です。

また、Aは5桁の数の先頭なので1以上です。
これは、Aは数字0の個数も表しているので、同時に数字0も1個以上あることを意味します。

0が1個以上あるということより、1、2、3、4の数字はあわせて4個以下しか使われていません。
さらに、その使われているA、B、C、D、Eの合計は5と決まっているので5つの数字の組み合わせは、

（0、0、0、1、4）（0、0、0、2、3）（0、0、1、1、3）（0、0、1、2、2）（0、1、1、1、2）

の5通りしかありません。

この中（0、0、0、1、4）は、「4」に着目すると、4つ使われている数字は明らかにないので不適。
同様に（0、0、0、2、3）も「2」に着目すると不適、
（0、0、1、1、3）も「3」に着目して不適、
（0、1、1、1、2）も「2」に着目して不適。

よって（0、0、1、2、2）を問題文の条件どおりに並び替えた21200が求める数になります。

答え：21200

短い問題文ですが、題意を非常にとらえにくくなっています。

「5桁の数ABCDEの各位の数A、B、C、D、Eは、
同時にA、B、C、D、Eの中にある0、1、2、3、4の数字の個数を表している。」

という分割して考えにくい2つの条件を整理して、チェックする姿勢にたどり着けるかどうかが分かれ目になっています。

後半の条件は数式化しやすく（A+B+C+D+E＝5）、
それを土台にして前半部分の突破口である「Aは1以上、
同時に0は1個以上」から手をつけていきます。

～今回の問題より導かれる出題校からのメッセージ～
日本語で書かれた見にくい条件文をきちんと理解し、整理することが必要です。

灘中の入試では、非常に短い問題文の中に隠されている複数の条件を、「使える形」で瞬時に整理する力が問われます。

コツは、どの日本語を既に使ったかどうかを明確にしておくことです。

本問では、ほとんどの生徒が、まずA+B+C+D+E＝5という条件を見つけることになるとおもいます。
ここで問題文を離れ、書き出しや当てはめを始める生徒がよく見られますが、
「問題文の5桁の数は一万の位から順にABCDE」を処理できていないのです。

一つ一つの日本語を精査する読解力。

算数の短問の中においても重要となるのはやはり国語力です。

東邦大学付属東邦中より。概算と精査の組み合わせです。

となるように、□の中に1から9までの異なる整数をあてはめます。このとき　ア、イ、ウ　の合計はいくつになりますか。

ア、イ、ウが同じ数だとしたらいくつになるでしょうか。

ア、イ、ウが同じ数だとしたら３です。

つまりア、イ、ウが異なる場合、すべて3以上の数にすると合計が1に満たないことになります。
（例えば1/3+1/4+1/5は1に満たない。）

よって、ア、イ、ウのうち一番小さい数は2であることがわかります。これをアとします。

よって残りの2つの分数の和は1/2となります。

ここで、先程と同様にイ、ウが同じ数だとすると4となります。
つまりイ、ウが異なる場合、ともに4以上の数にすると合計が1/2に満たないことになります。
（例えば1/4+1/5は1/2に満たない。）

よってイ、ウのうち小さいほうの数は3となります。
これをイとすると、ウは6になります。
3つの数の合計は2+3+6=11

答え：11

初見だとしたらかなりの難問です。

「同じ数だとしたら」すべてが3となること。
3つ異なる数ですから小さい順にア＜イ＜ウとなること。

そこから最初の2を見つけることが突破口です。
与えられた条件をひとまず無視して計算をして、そこから条件にあわせて微調整していくという手法はつるかめ算などにも共通する技術です。
まずは「概算」で見通しを立てる。
方程式の通用しにくい中学入試ではとても大切なステップです。

～今回の問題より導かれる出題校からのメッセージ～
概算と精査のバランスが大切

本問のように一気に答えを算出する方法がない問題は、中学入試では多数出題されています。

ひたすら書き出していくしかなかったりするものもすくなくありません。

そんななかでも、書き出しの量を減らす工夫はとても大切です。

大雑把に答えの周辺にあたりをつけてみることで、明らかに不要な部分を省略することができます。
また、とりあえずの計算をしてみることで、答えが大体どれくらいの範囲におさまりそうなのかということも把握することができます。

「とりあえずやってみる。」

闇雲な第一歩がゴールへ近づく近道となります。

栄光学園中より。与えられた条件の意味を掘り下げる力が問われます。

20名のあるクラスで次のような方法で席替えを行いました。
（１）くじで２人１組のペアを１０組つくる。
（２）そのペアになった２人の間で席を入れ替える。
（３）（１）、（２）をもう一度くりかえす。
席替えをした後も席替えをする前と同じ席に座っている生徒が１１名になることはありえません。その理由を答えてください。

(栄光学園中）

ありえないとされる「１１」という数字の特性に着目してみましょう。

１回目の（１）（２）の席替えで必ず全員が自分の席を離れることになる。
２回目の席替えを考える。

ある人が元の席に戻るためには、
１回目終了時点で元の自分の席に座っている人、
つまり１回目の席替えでペアになった人と２回目の席替えでもペアにならなくてはいけない。

このとき、相手も元の席に戻ることになる。
つまり、２回目の席替えである人が元の席に戻るということは、
１回目の席替えの相手も元の席に戻ることを意味する。
よって２回目の席替え終了時点で、
元の席に戻る人数は必ず２人の倍数になるので問題の「１１人」は該当しない。

「どんな方法によっても」１１人がありえないことを説明するというのは、コツが必要です。

A）すべての方法を試して１１人という結果がないことを示す。
B）「１１人」という個別の数字ではなく、
「奇数はありえない」「過半数はありえない」など「１１」のもつ特性に着目して証明の目標を緩くして論証する。

のどちらかです。
A）を稚拙だと決め付けてはいけません。高々数十通りの可能性であればそのほうが完結な場合もあります。
今回は、B)です。ほとんどの受験生が２回の席替えの場合の数はかなり多いことを容易に想像すると思いますので、
B)の方針で検討したことかと思います。

「すべて」「かなら」の証明にはある程度の習熟が必要ですので、
身の回りや通常のディスカッション・説明の機会を活かしていくことが大切です。

～今回の問題より導かれる出題校からのメッセージ～
論点を適宜変形していく力が大切

証明は中学生の範囲ですが、
論点の整理と論証の方向付けの能力というものは小学生に対しても十分に問うことの出来る分野です。

本問で問われているのは
「とあること」を証明するということは、何を意味するのか。
ということを掘り下げる力です。

直接は説明できなくても、同じことを意味するものを見つけ出し、
そちらの説明へと方針を転換する。

身近なものでは対偶をつかった証明など「間接的な」証明能力が問われる場面は少なくありません。

与えられた条件を様々な角度から検討し、知識を動員して同値なものに確実に変形していく力は、
未知の問題を身近な問題に引き寄せる能力としてまさに応用力そのものと定義できます。

本問はその力を測る良問ですし、同じ形式を出題し続ける本校が最も大切だと考える能力であることを宣言している問題ともいえます。

親和中より。隠れた制限を見抜く力が求められます。

りんごとみかんの2種類の果物があります。りんごとみかんを1個ずつとって，皿に盛っていくと，どちらかがなくなったので，残った果物の1個ずつに，はじめにあったりんごの数だけのキャラメルを合わせて皿に盛っていきました。果物がすべてなくなるまでに，キャラメルは全部で153個使いました。はじめに，果物は2種類合わせて，最も多くて何個ありましたか。
また，最も少なくて何個ありましたか。

(親和中）

「1個ずつにキャラメルを何個かずつ対応させると153個になる。」は、大きな制限を与えています。

1回に盛られるキャラメルの数をN個とすると、
それを何回か繰り返す、つまり何倍かすると153になるということです。
これはNが153の約数であることを意味します。

153を素因数分解すると3×3×17となります。
よって1回に盛られるキャラメルの個数の候補は1、3、9、17、51、153のいずれかです。
これはりんごの個数の候補が1、3、9、17、51、153であることを意味します。

また、盛られた回数はりんごとみかんの差を表しています。
キャラメルの個数が1個のとき、盛られた回数は153回。

同様に
3個のとき51回、
9個のとき17回、
17個のとき9回、
51個のとき3回、
153個のとき1回
であるから、

りんごとみかんの個数の差の候補は りんごの個数が
1個のとき153、
3個のとき51、
9個のとき17、
17個のとき9、
51個のとき3、
153個のとき1となります。

よってりんごとみかんの合計を考えると、最も少ないのはりんご17個みかん8個の25個。
最も多いのはりんご153個みかん154個の307個。

答え：最少25個、最多307個

どこから手をつけてよいかがわかりにくい問題です。


153の素因数分解により約数が6個しかないことを発見できると、
作業量に見通しがつき手が進むことになります。

本問はキャラメルは整数個であること、
そして何回か「繰り返した」結果が153個であるということが
1回に盛られるキャラメルの数の候補（つまりりんごの個数の候補）に大きな制限を与えているのです。

最後のポイントは、キャラメルの盛られた回数は「差」を表しているだけで、
りんごとみかんのどちらを多くするかは決定されていないという点です。

最少ではりんごが多く、最多ではみかんが多くなっているという点が最後の注意力が求められる点です。

～今回の問題より導かれる出題校からのメッセージ～
隠れた制限を見つけ出す力が大切

本問は「りんごの数と同じ数のキャラメルを繰り返し皿にもったら153個になった。」
という文章の分析にたどり着くかどうかが大きな分かれ目となります。

とても複雑であいまいな日本語を、厳格な数的条件へと読み換える力です。

これは、普段から与えられた問題文を、
常に「式で考えると？」「図で考えると？」といった視点でチェックする姿勢が必要になります。

当日気付くために必要なのは、運やひらめきだけでなく、
普段からこのような姿勢をとる習慣をつけておくことです。

ラサール中より。パターンを生み出す基本原理を見つけ出す力が問われます。

１もしくは2を小さい順に左から並べて、ある整数を1と2のみの和として表すことを考えます。例えば、5という整数については1+1+1+1+1、1+1+1+2、1+2+2の3通り考えられます。このようにして2006を1と2のみの和として表すとき、その表し方は何通りありますか。

(ラ・サール中）

順序は自動的に決まりますので、それ以外の部分にのみ着目すればよい問題です。

小さい順に並べるので、場合分けされるのは1と2の個数によってのみであることに着目する。
2の個数は最大でも2006÷2＝1003より
2+2+・・・・・・+2という形で1003個。

つまり2の個数は0から1003個までの1004通り考えられる。
よって、2006を1と2の和で表す表し方は1004通り。

答え：1004通り

問題に例示されている5の表し方は、
2の個数を1つずつ増やすことでパターンを考えていけるというヒントです。

1の数に着目しても、５個、3個、1個という形で見分けにくくなりますが、場合の数は求まります。

あるものを様々な形で表させる問題のポイントは、
それぞれの表し方の間にある関係性に注目することです。

本問では2つの「1」が1つの「2」に変換されますので、
それぞれの個数に着目しながらパターンを考えます。

～今回の問題より導かれる出題校からのメッセージ～
パターンを生み出す原理に着目することが大切

場合の数の基本は、「もれなくだぶりなく」です。

「広い視野」が必要になりますが、そもそもなるべく「広く」考えるのは当然の姿勢ですから、
具体的に身につけられる着眼点が必要になります。

それは、漠然と数えるのではなく、パターンを生み出す原理を見つけることに集中することです。
やみくもに見つけようとするのではなく、スタート地点と基本原理を見つけ、
あとは機械的にパターンを作り出していくことが大切なのです。

本問はある程度の書き出しや問題文での例示から、
基本原理である「2つの1と1つの2の交換」を見つけ出すことではじめて「1004通り」という膨大な数にたどり着けるのです。

～今回の問題より導かれる出題校からのメッセージ～
知識をストックすると同時に、思考の基本フレームを意識する。

個々の知識をストックする機会は多いのですが、思考のフレームをストックすることがなにかと少ないのが、

中学受験という現場です。

丸暗記学習を悪者扱いするあまり、思考フレームのストックまでもおろそかにされてはいませんか。

十把一からげに「暗記は悪！」といっていては脳が成長しませんよ。

おそらく開成中学の受験生は全員「二酸化炭素は水に溶けやすい」ということを知っています。

「二酸化炭素は水に溶けやすい」という知識と、

「大気の二酸化炭素は意外に増えていない」という事実・現象を結びつけるものが、

選択肢の洗い出し→仮説検証という思考技術です。

理科に限らず全科目において、そしてなんだかの問題・課題を解決するために不可欠のテクニックです。

未知の問題に出会ったとき、とりあえず、登場する事象の構成要素を書き出し、そのそれぞれを検証するという方法を身につけるよう意識してみてください。

灘中より。粘り強い類推能力が問われます。

5桁の36の倍数で、２、３、５のどれもがいずれかの桁にあらわれる整数（例えば53928など）のうち最も小さいものを答えよ。

(灘中）

テーマが「倍数と見た目の関係」であることに気づくことが突破口です。

36の倍数であるということは、36＝4×9より、4と9の倍数でもあるということです。

9の倍数は、各桁の数字の和が9の倍数となっています。

5桁のうち２、３、５の合計１０はすでに決まっているので、
残りの2つの数字は合計８もしくは１７となります。

合計８から考えると（１、７）（２、６）（３、５）（４、４）
合計１７から考えると（８、９）
が候補になります。

また、4の倍数は下2桁の数が4で割りきれる数である。

最小のものを求める問題なので（１、７）で１を一万の位にもってくることから検討をする。

すると、残りの２、３、５、７から下2桁に4の倍数である72をつくることができるので、
求める数は13572であることがわかる。

答え.13752

倍数判定は、一般に２、３、５などの（大きくても13ぐらいまで）の知識しか習いません。

しかし、基本的な方針や組み合わせることの例示などで
比較的簡単に応用力をつけることができる分野でもあります。

問題の形式が見慣れないものになっていますが、
本問は「倍数判定」の問題であるという見当をつけることがスタート地点です。

あとは、誰もが知っている知識の組み合わせと効率的で論理的なしらみつぶしです。

～今回の問題より導かれる出題校からのメッセージ～
作業量を概算し、見通しを立てるという思考が大切

本問では大きな差はでませんが、解説にあるような「作業量の概算」はとても大切な技術です。

時間制限のある試験において、そもそもその手法の作業量に現実味があるのかどうかを判断する力です。

不適格であれば、他の手法を探すことになります。
このような効率的な状況判断をもたらしてくれるのが「作業量の概算」です。

解説を読んでみると、「書き出せば一番速かった。」ということや、
「既に書き出してはいたがそもそも無理な量だった。」という経験が誰しもあるかと思います。

見通しを立てる冷静な思考によって、必要となる時間が大きく異なってくる良問でした。