対称性を利用する 2010-09-14
対称性を利用する【対象学年:4年生以上】

1-9までのカードが、一枚ずつあります。
このカードを並べて3桁の数を作ったとき、十の位が一番大きく、つぎに百の位、一の位の数字が1番小さくなるような並べ方は何通りありますか。

まずは、書き出してみましょう。
また、あることに気づくと解くのがぐっとらくになります。

84通り

(解法1)
十の位、百の位、一の位の順に数が大きいのですから、その順に樹形図などを使って整理していきましょう。
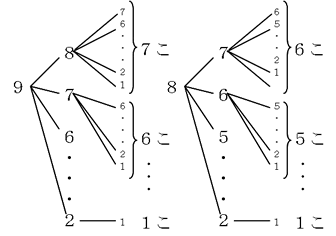
そうすると、十の位が「9」のとき、7+6+5+…+2+1=28通り
十の位が「8」のとき、 6+5+…+2+1=21通り
同様に、十の位が「7」のとき、 5+4+…+2+1=15通り
「6」のとき、 4+3+2+1=10通り
「5」のとき、 3+2+1=6通り
「4」のとき、 2+1=3通り
「3」のとき、 1通り
となります。
十の位が1または2の場合は百、または一の位が十の位より大きくなってしまうため、ありません。
よってこれらすべてを加えると、84通りとなります。
(解法2)
実はこの問題に関しては、9×8×7÷6=84という式でも求められます。
理由は以下の通りです。
1枚の1~9までの数字を並べてできる数字は全部で9×8×7通りあります。このうちどの3枚を選んだときも、百の位、十の位、一の位の数字の大きさは(百,十,一)の順で、
(大・中・小)(大・小・中)(中・小・大)(中・大・小)(小・中・大)(小・大・中)の6通りができます。
このうち問題の条件を満たすものは1つだけですから、全体を6で割ると答えが出ます。
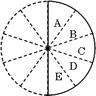
このように、ある条件を満たす複数のものが、均等に散らばっている状態を「対称性がある」といいます。円卓に人が座っていくような場合などにもこういった考え方で、全体を均等に割れば答えが求まったりしますね。
また、この問題では、1~9までの数字から3枚を選んだとき、その3枚の並び方のうち、条件を満たすのは1つだけですから、結局
「1~9から3枚選ぶ選び方が何通りあるか」という組み合わせを求めるのと変わらないことになります。
こういった問題文の読みかえ、言いかえも重要な考え方のひとつです。
-------------------------------------------------------------------------------------------------------
~2箇所でブログランキングに参加しています~
1.
2.![]()
-------------------------------------------------------------------------------------------------------
ところで、こんなのはじめました。
参考書選びの参考にご利用ください。
ロジム2階参考書コーナー
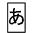 と表すことができます。
と表すことができます。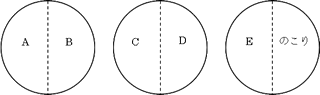
 とったことになります。
とったことになります。
 こに分けた1つぶんなので
こに分けた1つぶんなので 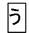 となります。
となります。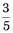

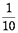
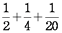
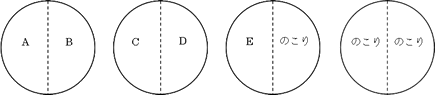
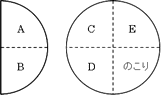

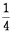
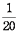 となります。
となります。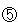 とすると、Aは
とすると、Aは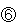 、Cは
、Cは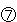 -3人、Dは
-3人、Dは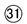 -10人
-10人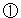 は4人、5人、6人の3通り。
は4人、5人、6人の3通り。