学習塾ロジム　今週の1問by 学習塾ロジム

今週は東邦大東邦中より1問です。

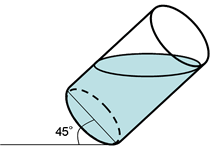
直径10ｃｍ、深さ30ｃｍの円柱の容器いっぱいに水が入って います。
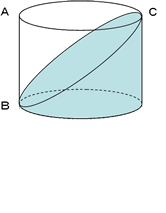
この容器を下の図のようにゆっくり傾けました。
容器を45°まで傾け、もとに戻したとき、容器の中に入って いる水の深さは何ｃｍになりますか。　　　　　（東邦大東邦中一部改）

単純化できないか考えましょう。

下の 図のように真横から見て考える。
傾けたときの水面と、地面は平行になるので、三角形ＡＢＣは、直角二等辺三角形となる。
ＡＣ＝10ｃｍであるから、ＡＢも10ｃｍとなる。

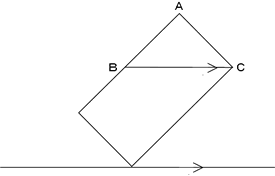
ＡＢ＝10ｃｍとしたとこ ろで、こぼれた部分の体積を考える。
下の図のよう に、高さをＡＢ＝10ｃｍ、底面の直 径10ｃｍの円柱を考 えると、
こぼれたのはこの半分にあたることがわかる。

よって、こぼれ たのは、5×5×3.14×10÷2＝392.5cm
残った水の量 は、5×5×3.14×30－392.5＝1962.5cm
もとに戻したと きの高さは、1962.5÷（5×5×3.14）＝25cm
（答え）　25cm

立体の問題の中に、角度が含まれている問題で す。
空間座標を学んでいない小学生の場合、
この条件から
「平面図形に持ち込もう」

という方針をしっかりとたてられるように勉強内容を整理していることが必要です。

ここをクリアーしたあとは、「こぼれた部分が、円柱の半分である」という求積の方針ですが、
これは受験までに必ず類題に出会うものですから、問題はないでしょう。

～今回の問題から導かれる出題校からのメッセージ～
・複雑な事象の単純化・検証能力が大切である

ここまで「理系研究者に必要な能力を問お う」
という姿勢が顕著な学校もなかなかない東邦大学東邦中の出題です。

類題は、ここ何年かで筑波大附属などでも見られていますが、
解答の単純さほど簡単に解けるものではありません。

かつての中学受験生と比べ、最近の生徒に大きくかけていると感じる能力の一つが

「言い換え」「モデルの変形」

といった単純化の能力です。

単純化は、その場その場での試行錯誤と、検証能力が伴わなければ実現できませんし、
なによりもそこまでねばり強く考える時間を取れていないことが原因かもしれません。

多くの問題にあたり、高いパターン認識力を鍛えることで、
たとえ最難関校であっても合格するレベルを確保するのは難しくありません。

ただ、この試行錯誤→単純化→検証というサイクルを身につける良問に取組む
貴重な機会を見逃してしまうはあまりにももったいありません。

理系研究者だけでなく、最前線で活躍する社会人にとって必要な力を問いかける良問です。

今週は函館・ラサール中より1問です。

AB=1cm、BC＝1.5cmの三角形ABCにおいて、角 BACの大きさは、角ACBの大きさの2倍です。
この三角形ABCをADを折り目として折るとBとEが重なります。
次の問いに答えなさい。
（１）CDの長さは何cmですか。
（２）ACの長さは何cmですか。
（３）角DECの大きさは角ACBの大きさの何倍ですか。
(函館ラ・サール）

相似の問題です。

「こ の三角形ABCをADを折り目として折るとBとEが重なった」という問題文の設定より、
三角形ADEと三角形ADBは合同なので、角EAB＝角DABとなる。

これと「角CABは角ACBの2倍である」という条件を合わせて考えると、
角ACB＝角EAD＝角BADとなる。この角の大きさを下の図に「○」で表すこととする。（図1）

ここで、角ADBは、三角形ADCの外角であることから、角ADB＝角CAD+角ACDとなり、
○×2の大きさとなる。
また、折り返したという設定より、角EDAも同じく○×2の大きさとなる。（図2）

さらに、角EDBは、三角形CEDの外角であることから、角EDB＝角CED+角ACBとなる。
角EDB＝○×4、角ACB＝○×1であるので、角CED＝○×3となる。（図3）

（１）三角形ABCと三角形DBAは、2つの内角が等しいので相似である。
三角形ABCにおいて、AB：BC＝1：1.5であるので、三角形DBAにおいてもDB：BA＝1：1.5である。
BA＝1cmであるから、DB＝1×2/3=2/3cmとなる。
よって、CD＝1.5－2/3＝5/6cmとなる。
（答え）5/6cm

（２）下の図より、三角形ADCはCD＝DAの二等辺三角形である。
よって、（１）よりCD＝DA＝5/6cmとなる。
DA＝5/6を、三角形ABCと三角形DBAの相似の中に当てはめると、
AC＝DA×3/2=5/6×3/2=5/4=1.25 cmとなる。
（答え）1.25cm

（３）下の図より、
（答え）3倍

本問は、解答の下線部である、

「2つの内角が等しいから」相似

という知識を使いこなせるレベルで定着させているかどうかがすべてを握っています。

中学入試ではあまりみかけないタイプの相似で す。
これは、
「2つの三角形が相似となる3つの条件」
をしっかりと頭に入れていなければ気付くことができません。

多くの生徒は、俗に言うピラミッド型と砂時計型の相似にしか気付けません。

そして、「なぜ相似といえるか？」という問い に正確に答えられる生徒も少ないのが現状です。

「相似ならば～」についての練習は数多くこな しているのですが、「～だから相似」については全く見逃されているのが現状です。

合同とあわせて、成立 条件をきちんと整理して、
合同・相似の発見、証明に取組んでおかなければ、
本問のような相似を見つけることは絶対に不可能でしょう。

「雑多な情報の中から、既存のフレームと比較し、適応可能なものを探し出す。

というものがあります。

そもそも「自分が解けるものとは、どのようなものなのか」がわかっていない生徒が、
「自分が解けるもの」を見つけられるはずがありません。

このタイプの問題は、解説を読めば必ず「あ、そうか。」と理解したかのような感覚に陥りがちですが、
問題は「その場で気付けなかった」という事実です。

「なぜ気付けなかったのか。」

それは、往々にして「いま探すべきものについての定義が明確にはわかっていない。」ことが原因なのです。

今週は高知学芸中学より1問です。

下の（あ）～ （え）は同じ立方体の展開図です。（い）（う）（え）の展開図に残りの数字を、向きに注意して書き入れ、展開図を完成させなさい。（高知学芸中）
（あ）
（い）
（う）
（え）

方向感覚が狂わないように、工夫してみましょう。

（い）
（う）
（え）

（あ） のように、上下左右をきちんと記入します。
（い）で考えるときには、○の部分は明らかに3の右と一致します。
（あ）では、3の右と接しているのは4の左なので、方向が確定します。
このように、立体図形や平面図形の移動、折りたたみの問題において、
方向を常に正しく把握するためには、丁寧な作業が重要です。
（あ）
（い）
万が一にも間違えたくはない問題、しかも確認が難しいタイプの問題では、
このような面倒でも確実な工夫が、見直しを含めると一番の近道になるのです。

～今回の問題から導かれる出題校からのメッセージ～
・ 確実性を担保する視点を見つける能力が重要

「見直しをする力」これは、注意力などケアレスミスをなくすための能力にとどまらず、
「その観点から計算してみても成立していれば答えに誤りはない」
という自らの解法とは別の観点を見つける能力のことです。

確実なものは何か、不確実なものは何か。

そして、その不確実性はどの観点からの確認で払拭されるものなのか。

見直しは、自らの計算の足跡をなぞるものではありません。

考え得る様々な視点で検証する姿勢こそが、
未知の分野を切り開く人間に必要な能力なのです。

100％確実なものと、99％以下のものをきちんと見分ける。
100％確実なものを根拠とする姿勢を身につける。

「センス」「ひらめき」による筋道を、確実なものとする論理性。

レベルの高い学校ほど、「柔軟な発想による方針策定」と
「地道な検証」の両方を必要とする問題を出題してきます。

今週は慶應中等部より1問です。

下の図のように、1辺が15cmの正方形ABCDとおうぎ形ABDがあります。点Eは、辺AB上にあり、色のついた2つの部分の面積は等しくなっています。このとき、AEの長さを求めなさい。
円周率は3.14とします。

　（慶應中等部） 　

「明らかに測定不可能な面積の差について 考える問題」といえば。。。

下の 図のように3つの部分を（ア）、（イ）、（ウ）とおきます。

（ア）＝（イ）なので、それぞれに（ウ）をたして、
（ア）＋（ウ）＝（イ）＋（ウ）も成立します。
（ア）＋（ウ）の面積は、半径15cmの円の4分の1なので
15×15×3.14÷4＝176.625
となり、これが（イ）＋（ウ）である台形AECDの面積となる。
よって
（AE＋15）×15÷2＝176.625
という式が成立し、これをとくと
AE＝8.55cmとなる。

答え　8． 55cm

平面図形内での、面積の差、和についての問題 です。

しっかりとした基礎演習をもとに、

「二つのぬられた面積の測定は無理である。」
「三角形EBCの辺EBを導き出すのは無理である。」

という決断をできる かどうかが大切です。

また、和の問題、差の問題では実数が求まることはほとんどありません。
この点に着目すると、方針の選択肢はせばまり ます。

同様の問題（正方形の中に直角三角形が向かい 合って入っているもの）
に4年生で出会っているはずです。
その問題をきちんと抽象化しておけるかどうか が分かれ目でした。

～今回の問題から導かれる出題校からのメッセージ～
・基本問題の整理能力を鍛えよう

基本問題を応用力を持たせるかたちで整理できているかどうかが問われています。

首都圏上位校の中では、 女子学院とならんで算数が基本問題の高い処理能力をもとめる形式となっている慶應中等部ですが、単純な繰り返しだけでは、対応できません。

基本問題＝簡単な問題ではありません。

その先に、多様な応用問題が考えられる土台となる考え方が含まれている問題が
ここで問われる”基 本問題”なのです。

なぜ、基本問題といわれるのか。
その裏に隠されたとても大切な考え方は何か。
そして他分野ではどのように使われているのかなど、
反射的に解けるだけ ではなく、自ら情報を判断し、整理する力が問われています。

じっくり取り組ませる問題の多い他の上位校に比べれば、
「算数が不得意でもなんとかなる」ということはありません。

ハイレベルな受験生の中では、すぐに差がつき ます。
灘中1日目なども同様ですが、
基本問題の基本たる所以をしっかりと考え、
噛締めていくべきだというメッセージが込められた良問です。

今週は東邦大学付属中東邦より1問です。

下の図のように左から順に正方形をならべ、各頂点を結んでいきます。この直線（対角線）について次の問いに答えなさい。
（１）4枚目をならべると、3枚ならべたときよりも直線は何本増えますか。
（２）7枚ならべると、直線は全部で何本になりますか。
（３）直線が150本を越えるには、少なくとも何枚の正方形が必要ですか。

（東邦大学付属中東邦）

(2)までの結果をしっかりと考察してみましょう。

正方形の枚数と直線の本数を表にしてみると下のようになる。

正方形の枚数がｎ枚のとき、直線の本数は
n×(n+1)　本
となっています。

(1)表より、
20-12=8
答え 8本

(2)上記の式において、nが7の場合を考えると
7×(7+1)＝56　　
答え 56本　

(3)
nが11の場合　　
11×(11+1)=132
nが12の場合
12×(12+1)=156
よって
答え12枚

見抜く力と同時に、
・すばやく整理し規則性の発見のための考察
・検討に時間を割くという思考プロセス
が身についているかどうかが勝負の分かれ目です。

そもそも理系志向の強い生徒が集まる学校です。
こういった問題に、粘り強く取り組む姿勢は身につけておいてほしいものです。

本問のように、規則性を見たことのない式で表さなくてはいけない問題は近年頻出です。
「nを使っ た式であらわせ」という出題もかなり見られるようになりました。

まず多くの漸化式タイプの問題に当たっておくことが大切です。
規則性のパターンは、高校生でも手を焼くぐらい様々なものが考えられます。

少なくとも典型パターンだけは頭に入れておいたほうが良いでしょう。
「漸化式を作る」という意識付けもとても大切な要素です。

合格最低点という考え方では、（１）と（２）でどうにかなるものですが、
普段の思考トレーニングとしてしっかりと取り組んでおきたいタイプの問題です。

きちんと表にしたり、「見やすい形に整理する」ことは、「気付き」が重要となる本問においてはとても大切なものです。論 理の積み上げだけでなく、「見やす くすることで、ある突破口に気付く」というアプローチは、中学受験においてとても大切な身につけておいて欲しいものです。

～今回の問題から導かれる出題校からのメッセージ～
・初見の事象に対し粘り強く考察する力が大切です。

理系教育に力を入れていると公言する東邦大学附属東邦中学校。
その言葉通り、理科系研究において最も基本的な能力である「粘りづよい考察力」を問う良 問です。

（１）と（２）は、丁寧に見やすく（この作業の正確さも、理系として必須の能力ですね。）書き込んでいけば全く問題ありません。
（３）が問題です。
1枚目～7枚目まで（鋭い生徒は4枚目まで）の結果を元に、法則を見つけ出さなくてはいけません。

本問は図形の範囲ではなく、数の規則性、数列で言う漸化式の問題です。
ｆ(n)=n×(n+1)を導き出すのは、そう容易いことではありません。
（もちろん、nというパラメーターの概念がなくても、□や？等と置くなど、小学校中学年の生徒でも
回答可能です。）
そもそも図形が前面に押し出されていること、そして図形内の直線の複雑さにかなりの受験生が圧倒され、とばしてしまいがちです。

（１）と（２）の誘導により、かなり易しくなっています。（１）、（２）で、書き出し可能な範囲の問題により誘導し、（３）で何百番目というような、規則 性を活用しなくては対応できない問題を出すというのは典型的な流れです。
試験当日はともかく、折角の受験勉強の過程においては、このような実験考察問題に時間をかけて取り組んでいくことは貴重な体験となるのではないでしょう か。

今週は雙葉中入試より1問です。

太郎さんはA町から一本杉を通って山頂Bまで登るのに１時間２０分、山頂Bから一本杉を通ってA町まで下るのに５５分かかります。ある時A町から山頂のB まで登るのに、一本杉と山頂のちょうど真ん中の地点で忘れ物に気が付きすぐ町までもどりました。そして忘れ物をとり、すぐ山頂へと向かい、はじめに町を出 発してから３時間５分後に山頂に着きました。もしも一本杉で忘れ物に気づいていたら、かかった時間はいくらだったでしょうか。太郎さんは登るときと下ると きはそれぞれ決まった速さで歩きます。

（雙葉中）

求めたい部分の距離の比を明らかにしてくれる ものは、時間の比しかなさそうです。

わすれものに気付いた地点をCとして考えます。
かかった時間より距離の比が求まる。

AB往復：80+55＝135分
AC往復：185-80＝105分

よって、AB：AC＝105：135＝7：9となる。

図のように距離の割合を考えると、
CBの割合は
9-7＝2
となり、Aから一本杉までの割合は

9-2×2＝5
となる。

よってA～一本杉間を往復するのにかかる時間は
105×5/7＝75分

求めるべきは「A～一本杉間往復＋A～Bの上り」なので
75＋80＝155分

答え　2時 間35分

速さと比の難問の典型例です。
雙葉中は処理能力だけでなく、かなり深く、丁寧な読み解きを要する問題を出してきましたが、女子校ではかなり重い部類の問題に入るでしょう。

ポイントは、

「求めたい片道の距離の比は、往復の距離の比と同じであり、往復にかかる時間の比から求められる」

という考え方です。

距離、速さの問題は、使う要素が「時間・速さ・距離」の3つしかありません。
この3つが、様々な形で見えにくくされていることが、この分野の難問の典型かつ唯一の方式です。

本問のように、片道の距離の比を求めたいけれども、片道の時間の比は求まらないなど、
求めたい値と同じ意味をもつ値を的確にさがさなくてはいけません。

ただ、よく考えてみると当たり前。
目の前の比の値に引きずられ、数学的に解こうとすると行き詰りますが、頭の中できちんと人が動いているイメージを作るとすぐに気付けます。

「同じ距離を歩いた時間の比」と聞くと、同じ方向に向かって、同じ時刻に並走していることを想像しがちですが、時期が違っても、逆向きに歩いていても良い のです。
「必要な情報」について、要点のみをしっかりと把握することで、視野が広がってきます。　

～今回の問題から導かれる出題校からのメッセージ～
・数式と現実のイメージの結びつけを怠らないこと
算数の基本は、「数え上げ」と「測定」です。
つまり明確な対象がある場合がほとんどです。

「何を求めているのか。」「何を探しているのか。」に関して、
明確なイメージがなければ数えることも、測定することも不可能です。

にもかかわらず、勉強を進めていくと、とくにハイレベル勉強に進むにつれ、
数式のみを操作している時間が増えてきてしまいます。
常に、図式化することで数式だけでは表せない、
同値変形のヒントや言い換えのヒントを探るという、
算数を学ぶことの意味をきちんと教えてくれる良問です。

今週は灘中入試より1問です。

下の図 で、ACの長さは10cm、AFの長さは6cmです。
（辺ADの長さ）：（辺BDの長さ）＝3　：　2
（辺BEの長さ）：（辺ECの長さ）＝5　：　2
とするとき、図の角（ア）の大きさを求めなさい。

（灘中）

「角アを求める」はどこから手をつけていいのかわかりませんよね。まず、手持ちの選択肢を冷静に洗い出して みましょう。

下の図のように辺ABと辺CGが平行となるように、AEの延長戦上に点Gをとり、辺EGと辺GCという補助 線を引く。

すると三角形ABEと三角形ECGが相似　(相似比はBE:ECより5:2)　となる。
また三角形ADFと三角形GFCも相似となる。

AD:DB=3:2なので、AD:DB:GC=3:2:2となる。
よって、三角形ADFと三角形GFCの相似比はAD:GC=3:2となる。

以上よりAGの長さは

6×　（3+2）/3　　=10cm

となる。

ここでAC=10cmと問題文にあるので、三角形AGCはAC=AG=10cmの二等辺三角形となる。
錯角を利用し、角（ア）＝角G。
よって角(ア)＝角G=（186－46）÷2＝67度

答え　67 度　

解くための第一歩。それは
「そもそもこの角アなんてどうやっ たら求まるのか？」
としっかり立ち止まって、方針を考えるこ とです。

図形のなかのある角度の大きさが判明するときに必要な要素が
どのようなものなのかを精査してみることが大切です。

三角定規と同じ形の三角形や、正三角形、角度がわかっている二等辺三角形などはここには１つもありません。また３つの内角のうち ２つがわかっているような三角形も１つもありません。

ここまでしっかりと整理、チェックを進めて行くと

「どこかに 合同、相似の図形を見つければ、角アが判明するのではないか 。」

という突破口となる方針にたどり着きます。

～今回の問題から導かれる出題校からのメッセージ～
・出来ること、出来ないことをしっかりと見極める力が大切
本問は、1日目の問題です。
つまり1問あたり3分～５分で解き 進めなくてはいけない問題群の中の1問です。
何も考えずに、辺の比から面積比を求めたりし始めると泥沼です。

そもそも面積比から角度を求めることはとても難しいですし、
そのような問題に出会ったこともないはずです。
「とりあえず～」という浅い考えで動き始めると５分はあっという間です。

情報を精査して方針を決定するというレベルの高い判断力が求められています。

対策は、角 度の練習問題を数多くこなして行く中で、
解法を自分の中でしっかりと整理しておくことです。

そして、問題文を読んだ時に、
自分の考える解法を進める上で 十分な情報があるのか、足りない情報は何か、そしてその足りない情報はどこからか導き出せるのか
という思考回路が動き出すような日頃のトレーニングが大切です。
そうすれば、そもそも情報が足りずに行き詰まることになる解法にはまり込む危険性を回避できるのです。

一つ一つからしっかりと学んで行く問題演習が大切。

こなすこ とが目的になってきた受験生の勉強姿勢に警笛をならす良問です。

今週は麻布中学算数入試より1問です。

容器A に食塩水が400g入っています。これを空の容器BとCに200gずつ入れ、さらにBには食塩を10g、Cには水を100g入れてよくかき混ぜました。次 にB、Cから食塩水を210gずつAにもどしてよくかき混ぜたところ、最初と同じ濃さの食塩水ができました。この食塩水の濃さは何％ですか。ただし、濃さ とは食塩水の重さに対する食塩の重さの割合のことです。　　　　　　　　　　　　　　　　　　　　　　　　　　

（麻布中） 　　

「食塩水を混ぜる問題と言えば」で機械的に解き始めてしまうとお終いです。

容器Aの食塩水400gに含まれる食塩を【2】とおくと、（＊以下、【 】を用いて比を表す）
最初の作業で分けられた容器Bと容器Cにそれぞれ食塩が【1】ずつ含まれることになる。

ここで、容器Bに食塩を10g加えると結果として
（【1】＋10）gの食塩が容器Bの中に残る。

そして、容器Cに水100g加えると、食塩水全体は
200＋100＝300g
になる。この中に10gの食塩が含まれていることになる。

以上より、容器Bから戻される210gの食塩水の中には
【1】＋10g
の食塩が含まれ、
（容器Aには200＋10＝210gしか食塩水がないので、含まれる食塩はすべて戻される）
容器Cから戻される210gの食塩水の中には
【1】×210/300＝ 【0.7】
の食塩が含まれる。
容器Aに戻された食塩水は420gであり、
これが最初の食塩水と同じ濃さであるからこの戻された食塩水に含まれる食塩は
【2】×420/400＝ 【2.1】　　となる。

よって（【1】＋10g）＋ 【0.7】 ＝【 2.1】　　　という関係が成立する。
これより
【0.4】＝10g
となる。

はじめの食塩水に含まれていた食塩は【2】であるから、
10÷0.4×2＝50g
となる。
よって、食塩水の濃さは
50÷400×100＝12.5％
となる。

答え　 12.5％

この問題の難しいところは、一見普通の濃度の 問題に見えるところです。

この年（平成15年度）の麻布中の算数は、異例の1番小問題4問というスタート。
長いリード文と積み重ねていくタイプの小問が並ぶ
通常の形式とは違った出題に戸惑った受験生も多数でした。

小問ということですが、内容はさすが麻布中。
すべてがパターン解法では太刀打ちできないものでした。

問題をしっかり読み、条件を書き出す。その書き出し方も重要。
正確で用途にあった形の線分図など、問題文をよく読み、必要な形で整理する能力が問われています。
基本をあやふやにしたままに、
試行錯誤タイプの麻布対策だけをしてきた受験生を、きちんと落とす良問ぞろいでした。

本問は、なにも考えずに天秤図を書き出してスタートすると迷路に迷い込みます。
・時間経過に沿って出 来事を整理する。
・数式化して整理し、比較してみる。
という算数においてもっとも基本的な作業を丁寧に行うことが必要です。

～今回の問題から導かれる出題校からのメッセージ～
・麻布でも地道な作業をする能力は重視します。

御三家レベルでは、計算問題や小問は、受験生のレベルからすると必要ないと判断されることが多く、出題も少ないのですが、本問においては反射神経でとくだ けではなく、丁寧な作業を毎回きちんと、すばやく行うという気構えが必要だと言えます。

ここ数年、麻布中の算数は地道な数え上げや当てはめなどの地道な作業を伴う問題が多くなって気ました。もちろん、それぞれに高度なセンスが求められるもの ではありますが、かつてのような「ひらめき」への偏りはなくなっています。

麻布中志願者の典型的な志向として、洗練された切れ味鋭い解法を求めるというものがありますが、その質実な能力を 麻布中が求め始めたのは明らかです。

夢見る数多くの未来の麻布志願者に、麻布受験者になる覚悟を問うているともいえます。
あらゆる問題で丁寧な読み込み、精密な計算能力、書き出しと数え上げが求められます。

世間一般の自由・洗練なイメージのみで麻布中を志願している子供たちには、
一度取り組ませてあげることで麻布中の本当の姿を確認させることのできるメッセージ性のある良問です。

今週は開成中学入試より1問です。

40人 の生徒が、問題A・Bの2問からなるテストを受けました。得点は2問とも正解ならば10点、どちらか１問の正解ならば5点、どちらも不正解ならば0点です。その結果について次のようなことがわかっています。　　　　　　　　　　　　　　　　　　　
（ア）40人の平均点は6点でした。
（イ）得点が0点と5点の生徒はあわせて30人でした。
（ウ）問題Aを正解した生徒の人数は、問題Bを正解した人数の2倍でした。
問題 Aが正解で問題Bが不正解であった生徒は何人でしたか。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（開 成）

「重複」や「相当」を考える問題は、図式化することが必須手順です。

（イ）の条件より、AB正解の10点の人数は40－30＝10人だとわかる。
また、（ア）より40人の合計点が6×40＝240点であることが判明する。

以上より、5点をとった人数は、（240－10×10）÷5＝28人であることがわかる。
よって、AB不正解の0点は、40－（10＋28）＝2であることがわかる。

上のベン図で、上記の部分の人数が判明している。
また、（ウ）よりA正解：B正解＝②：①と置いている。
ここで、AかBの少なくとも一方を正解した人数は、40－2＝38であることがわかるので、
A正解＋B正解－AB正解＝38人であるといえる。
これを線分図で考えると　　

（Aを正解：②）＋（Bを正解：①）－（ABを正解10人）＝38人

よって
③＝48人
①＝16人
Aを正解：②＝32人
よってもとめるべきAだけ正解は
32－10＝22人

答え　22 人

算数を勉強することで身につけてほしい技術・ 思考法の中でも、もっとも大切な部類に入るのが数え上げです。
碁石や日付の数え上げ、場合の数など、
「一見して見えてくるものと、実際の数の差を把握する」
技術のことです。

すでに問題意識をお持ちの方もいらっしゃるかと思いますが、
上位中学校入試で苦手とする生徒の多い分野です。

この分野は、小学生にとって解き方に「気付く」ことがもっとも難しい分野なのです。
方程式をはじめとする数学知識を身につけた
中学・高校生でも、中学入試のこの分野の問題にはかなりてこずります。

突破口は、「きちんとした書き出しときれいな図式化」です。

数え上げのポイントは、
「重複する部分の発見」
と
「比の相当の発見」
です。

これらは、問題文や計算の中で気付くのはとても難しく、
具体的に図式化することで視覚で気付くことの方がとても簡単なことが多いのです。

正確で、きれいに整理された書き出しからは規則性を見つけやすく、
線分図をはじめとする図からは、
何と何が同じ量を表しているのかという「相当」を見つけやすくなります。

本問は、開成中入試問題の中でもかなり易問です。
ハイレベルな受験生が唯一陥る落とし穴は、数式のみで解こうとして時間をとられることです。
解答の線分図を書き出す（少なくとも頭のなかでイメージする）ことで、わずか数分で解答が可能です。

比の難問は、「相当」を見つけることが関門となります。
図式化することで、見つけやすくするという手順を必ず踏むことが急がば回ることにつながります。

～今 回の問題から導かれる出題校からのメッセージ～
・数字と条件の意味を正確に捉えることが重要

開成中に限らず、上位校の問題には付け焼刃的に習得した方程式等の、
指導要領範囲外の高度な算術が全く通用しない問題が数多く出題されています。

その学校の教務能力を披露する場とも言える入試問題において、
新機軸の
「基本的な項目に対する深い洞察力を要求する問題」

を作ることに力を置いている上位校ならではの問題です。

ポイントは、一つ一つの数字・条件の意味を深く、多面的に把握することです。
本問の条件「（ア）40人の平均点は6点でした。」に対して、
「40人の合計点は240点」という言い換えをきちんとしていくなどの基本的な作業のことです。

平坦な日本語で書かれた条件を、具体的な算数の言葉に置き換えたり、図式化するという、「問題文の意味を理解し、わかり やすく変換してつかいこなす力」が求められるのです。

普段から、問題に対して
「この条件から何がわかるのか」
「そもそも何が起きているのか」
を面倒くさがらずに、丁寧に確認する作業の積み重ねだけが、この力を養います。
ひとつの問題に対して、どれだけ粘り強く考察をし続けられるのか。
開成中の「強い」生徒を求める姿勢が見て取れる問題です。

今週は女子学院・算数入試問題からの1問です。

たて 135ｃｍ、横183cmの長方形の場所に図のように１cmの間をあけて、正方形のタイルをしきつめよう
と思う。タイルのしき方は４すみとも図のようになる。できるだけ大きな正方形を使うとすると、タイルの一辺は何cmになるか。また全部で何枚のタイルが必 要になるか。　　　　　　　　　　　　　（女子学院）

「公倍数・公約数」の範囲で、とても似た問題に必ず出会っているはずです。それらとの差は何なのでしょう か。

図２のように、隙間までふくめた正方形のタイルを敷き詰めることをかんがえる。
長方形のたてとよこをそれぞれ１ｃｍずつ広げて考えれば、
ここで算出された正方形のタイルの１辺が、
「求めるべきもの＋１ｃｍ」となり、
敷き詰められた枚数が、求めるべき枚数になる。
よって、
たて：135+1=136
よこ：183+1=184
という長さの長方形に隙間なく、正方形のタイルを敷き詰めることを考える。
この２つの数の最大公約数は8
よって、図２のように考えたときの正方形のタイル（斜線のもの）の1辺は8ｃｍ
これを図１で考えると、求めるべき正方形のタイルの1辺は
8-1=7
答え　 7ｃｍ

また、このとき必要となる正方形のタイルの枚数は
（136÷8）×（184÷8）＝391
答え391 枚

「たて、よこがそれぞれ15cm、18cmの長方形をなるべく大きな正方形に切り分け、余りがでないようにするとき、正 方形の1辺は何ｃｍになりますか。」
4,5年生が勉強する「公倍数・公約数」の範囲で、
最大公約数の考え方をつかった問題として必ず取り組む練習問題です。

本問とこの問題の類似性に気付き、違いを考えることがスタートとなります。

解き方、つまり隙間の処理の仕方は解答で示した1通りだけではありません、大切なのは
「邪魔な隙間をどうにかして処理することで、最大公約数の簡単な問題に変形できないか。」
という工夫に、時間をすべて費やすことです。

その中から、解答例のような処理のしかた等が、導かれるのです。

この問題を難しくしている要因はなにか。
言い換えれば、
この問題はどの基本問題を難しくしているのか。
という視点は、問題の本質を見抜く力として求められる技術です。

～今回の問題から導かれる出題校からのメッセージ～
・基礎知識をベースに、走りながら情報を取捨選択する瞬発力のある思考が大切

基本問題が多く、比較的高得点の争いになるのが女子学院中学校です。
しかし典型問題であっても、必ずひねった部分を付け加えることも忘れていません。

こうした問題をすばやく解き進めることのできる生徒は、
どこまでが基本でどこが解答を導きだす上でのボトルネックとなっているのかを判断する能力に長け、
余計な情報に時間をとられることがありません。

逆に、間に合わない生徒は、余計な情報の整理に時間がかかってしまうのです。

よく言われる処理能力とは、「鉛筆のスピードが速い、計算が速い」だけでなく「情報に対する優先順位付けがうまい」というものが含まれます。

典型問題が解説できるレベルまで完全に習得されていること。
そして、とりあえず思考を進めてみてボトルネックを確認すること。

じっと立ち止まって一本道の解答を検討するだけではなく、
すぐに走り始め、判断をし、余計な情報をそぎ落としながら解き進めるという思い切りの良さ。

女子校としては特に際立ってこの傾向が顕著な
女子学院中の求める人物像が見て取れる問題となっています。