学習塾ロジム　今週の1問by 学習塾ロジム

タイトル　2008-06-23

図を書いて試すのをためらったことはありませんか？

　下の図のような「あみだくじ」があります。これは、たとえば一番左のＡを選択した場合、図の太線をたどって左から４番目の位置に移動するものです。同じように、左から２番目のＢを選択すれば、左から３番目に移動することがわかります。このあみだくじについて、次の問いに答えなさい。

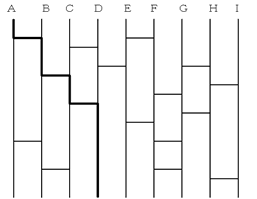
問１　Ａ～Ｉのうち、もとの位置よりも右に移るものはいくつありますか。
問２　このあみだくじをいくつか縦につなげて長いあみだくじを作ったところ、左から順にＡ、Ｂ、…、Ｉというように、はじめと同じ順番になりました。このとき、縦につなげたあみだくじは最も少なくていくつですか。

　ありません。

問１　５つ（Ａ、Ｂ、Ｃ、Ｅ、Ｇ）
問２　12個

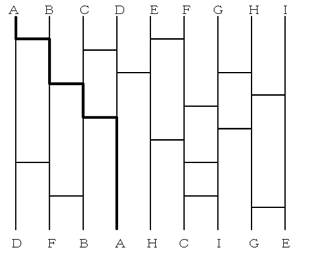
　ＡＢＣＤＥＦＧＨＩは、このあみだくじによって下の図のようにＤＦＢＡＨＣＩＧＥと入れ替わります。
つまり、このあみだくじを１回通ることで、次の表のように整理できます。

つまり、左から１番目→４番目→１番目→…と、ＡとＤは２回ごとにもとにもどります。
同様に、左から２番目→３番目→６番目→２番目→…と、ＢとＤとＦは３回ごとにもとにもどります。
さらに、左から５番目→９番目→７番目→８番目→５番目→…と、
ＥとＧとＨとＩは４回ごとにもとにもどります。

以上より、２、３、４の最小公倍数である12回で、すべてもとにもどるのです。

まとめ
　誰もが一度は触れたことのあるであろう、あみだくじを題材にした問題です。それぞれの線が交差することで、一見複雑な動きをしていそうなあみだくじですが、要はただの入れ替え問題に他なりません。解説の表のとおり、どことどこが入れ替わるのかを整理すればさほど難しい問題ではないでしょう。

　しかし、実際にこの問題に取り組んだ子供たちは、多くが途中で諦めてしまいます（小学生に限らず、中学生でさえもです）。この理由は以下の２点が考えられます。

1）点や線が多く、面倒臭がって意欲が減退するであろうこと
2）図が大きいため、実際につなげて試すことが困難であろうこと

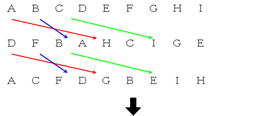
　過去にも、今週の一問で「調べ上げる」ことの重要性をお伝えしていますが、まさに本問も同様です。1）は学習姿勢に関係する避けがたい問題ではありますが、2）は工夫次第で容易に避けることのできる問題です。本問では、結局どこへ移動したのかさえ分かればよいので、下のように簡略した図で整理してみることが有効です（下の図では、例として１番目～３番目の移動先を図示しています）。このような工夫は、ぜひ経験から学び取って欲しいものです。

整数問題は、（整数という限定があるにもかかわらず）避けられがちです。

　０より大きい整数は、自然数とよばれます。そして、これらの自然数の多くは、連続したいくつかの自然数の和で表すことができます。たとえば、3＝1＋2、12＝3＋4＋5、100＝18＋19＋20＋21＋22などがその例です。これについて、次の問いに答えなさい。

(1) 98を連続した自然数の和で表すとどうなりますか。
(2) 1000以下の自然数の中で、連続したいくつかの自然数の和で表すことができないものはいくつありますか。

・奇数とはどのような自然数ですか？
・まったくイメージがわかなければ、とにかく調べることです。

(1) 11＋12＋13＋14＋15＋16＋17
(2) 10個

まず、偶数は2の倍数なので、必ず同じ自然数2つの和（□＋□）で表すことができます。
これに対し、奇数は偶数よりも1大きい数（□＋□＋1）ですから、
必ず□＋（□＋1）という2つの連続した自然数で表すことが可能です。
　
また、奇数の倍数（3の倍数、5の倍数、7の倍数、…）は、
等しい奇数個の自然数で表すことができるので、以下のとおり必ず連続した自然数で表すことが可能です。

3個　□＋□＋□→（□－1）＋□＋（□＋1）
５個　□＋□＋□＋□＋□→（□－2）＋（□－1）＋□＋（□＋1）＋（□＋2）
７個　□＋□＋□＋□＋□＋□＋□→（□－3）＋（□－2）＋（□－1）＋□＋（□＋1）＋（□＋2）＋（□＋3）

など…

　つまり、連続した自然数で表すことができない数は、偶数の中で奇数の倍数ではないものとわかります。
よって連続した自然数で表すことができない数は、素因数分解したときに奇数を含んではいけないわけですから唯一偶数の素数である2ばかりをかけあわせた数となります（1を除く）。

(1) 98は７の倍数なので、14＋14＋14＋14＋14＋14＋14→11＋12＋13＋14＋15＋16＋17と表されます。
(2) 1、2、4、8、16、32、64、128、256、512の10個です。

まとめ

整数問題は、難しいと思われがちですが、それは「調べる」作業を怠っている証拠です。
整数の問題は、特にことわりがなくても何か決まりがあるものです（そうでなければ問題になリません）。

この作業を面倒くさいと思うか、面白いと思うかは、大きな差であるといえるでしょう。

「勉強はつまらない」ではなく、
「何かの答えは自ら導き出してこそ意味がある」ことこそが勉強であることを知ってほしいですね。

公式は、理解してこそものになります。

　図１のような幅２cmの長いテープをさまざまな角度で多くの部分に切り分け、長さの同じ切り口どうしをつないでいきます（のりしろは考えません）。つなぐときの内側の角はすすべて180°より小さくなるようにします。これをつないでいったところ、図２のように１周してちょうどつながりました。この図形の外周の長さは117cm、内周の長さは99cmです。

　

　　　　　　　
問１　図２の図形の面積を求めなさい。

問２　図２の図形を、下の図３のように外周と内周ちょうど真ん中のところで２つに切り分けました。このとき、外側の部分と内側の部分（色つき部分）の面積の比を求めなさい。

そもそも、このテープの長さは何cmでしょう？

問１　216cm2
問２　25：23

問１　
テープを切り分けたそれぞれの台形の上底と下底に注目します。
図２のつなぎ方では、これらのうちすべて短い方をつないで内周、すべて長い方をつないで外周が作られています。
つまり、すべての台形の上底と下底の合計（下の図でのア＋イ）は、外周と内周の和の117cm＋99cm＝216cmとわかります。

よって、このテープの長さは、216cm÷２＝108cmです。
図２の図形の面積は、テープ全体の面積なので、答えは２cm×108cm＝216cm2となります。

問２　
外周と内周ちょうど真ん中のところで２つに切り分けた線は、テープを半分に切り分けた線になるので、その長さは108cmです。

ここで、図３の外側の部分、内側の部分ともに高さ１cmの台形の和と考えることができます。
まず、内側の部分は、
上底の和が99cm（図２の内周）、
下底の和が108cm（テープを切り分けた線）とわかります。

同様に、外側の部分は、
上底の和が108cm（テープを切り分けた線）、
下底の和が117cm（図２の外周）とわかります。

すべて高さの等しい台形ですから、面積の比は上底と下底の和で求められます。
これより、外側の部分：内側の部分＝（99＋108）：（108＋117）＝25：23になります。

まとめ 　問１について、最終的に面積を求めた式を思い返してみてください（２cm×108cm＝216cm2）。
何か気付く ことがあるでしょうか？　

２cmはテープの幅、108cmはテープの長さでありちょうど真ん中で切り分けた線の 長さでもあります。
つまり、図２の図形の面積は、図形のちょうど真ん中の長さ（センターライン）に
テープの幅をかけて求められているのです。
（幅２cmのローラーで、108cmまっすぐ引けば、塗られた面積はもちろん 216cm2になりますね）

この公式は、中学入試の世界でセンターラインの公式とよばれ、
主に図形の転がり移 動の問題などで重宝されているものです。

しかし、このような公式もむやみやたらに使っていては、本来使るはずのない状況で使ってしまう危険性もあります。
どのような場合に、どのような部分を求めるために使う公式なのかを、日頃から意識していろいろな公式とつきあっていってほしいところです。

「当選確実」、あなたは確実に処理できますか？

生徒数が480人の学校の生徒会で、４人の委員を決める選挙にＡ、Ｂ、Ｃ、Ｄ、Ｅ、Ｆ、Ｇの７人が立候補しました。開票数が410票になったところで１回目の中間集計を行うと、上位５名の得票数は下の表のとおりでした。この選挙で、無効票はなかったものとして、次の問いに答えなさい。

問１　第１回の中間集計で、当選確実となったのは誰ですか。すべて答えなさい。

問２　開票数が450票になったところで、２回目の中間集計を行ったところ、ＣとＤを除いた５名の得票数は下の表のとおりでした。このとき、Ｃが当選確実であるためには、最低何票獲得している必要がありますか。

数多く得票すれば当選確実ですが、そのラインとなるのは、むしろ「どれだけ少ない票で当選するか」です。

問１　ＡとＢ
問２　76票

問１　



まず、当選確実となるライン（最低得票数）は、

「これ以上自分に票が入らないにもかかわらず、ギリギリ（最下位で）当選できる得票数」を表します。



たとえば、得票数の多いＡを考えてみます。

Ａを当選させないとすれば、Ｂ、Ｃ、Ｄ、ＥがＡの得票数をこえて101票ずつ獲得しなければなりません。

つまり４人で404票必要です。



しかし、これまでのＢ、Ｃ、Ｄ、Ｅの得票数と残りの票数を合わせても335票しかありませんから、これはありえません。



よって、Ａの当選は確実です。





次に、Ｂを考えてみます。

Ｂが当選確実であるならば、Ｂにこれ以上票が入らなくても当選できるわけですから、

現時点で得票数が多いＡも間違いなく当選確実になります。



よって、残り２人の枠を、ＣとＤとＥで争うことになります。ここで、Ｃ、Ｄ、Ｅ合わせて（86×3＝）258票あればＢを敗れますが、これまでのＣ、Ｄ、Ｅの得票数と残りの票数を合わせても250票にしかならないため、やはりＢも当選確実です。





さらに、Ｃを考えてみます。この場合、残り１人の枠を、ＤとＥで争うことになります。ここで、Ｄ、Ｅ合わせて（71×2＝）142票あればＣを敗れます。そして、これまでのＤ、Ｅの得票数と残りの票数を合わせると180票になるため、Ｃは当選確実とはいえません。

問２　

Ｃの当選確実を考えるのですから、ＡとＢは無条件で当選確実です。



ここで、ＡとＢ以外の２人の枠をＣ、Ｄ、Ｅの３人で争うわけですが、これまでのこの３人の獲得票数と残り票数は合わせて225票です。



よって、（225÷３＝）75票を越えれば、この3人の中での最下位はありえません。

よって、票以上獲得すれば、間違いなく当選できるのです。

まとめ

　この先、○○が△△票とったとすると…と、いろいろ考えすぎてしまいがちですが、

いかに必要な人物を見極めて、それらの得票数とまだ開票していない残りの票数を考えられるかが重要になります。



　当選確実について、解説にもあった次の２点が大切です。

当選確実となるラインは、「これ以上自分に票が入らないにもかかわらず、ギリギリ（最下位で）当選できる得票数」であること

誰かが当選確実であるならば、その人物よりも現時点で得票数が多い人物の間違いなく当選確実であること

　１つ１つ整理しながら、何度も何度も考えてみる価値のある問題です。

ストッパーには、良問がそろっています（平成16年度　女子学院中学校より）。

下の図で、長方形ＡＢＣＤの辺ＡＢの長さは４cm、辺ＢＣの長さは８cmです。
このとき、対角線ＡＣを１辺とし、点Ｄを通る長方形ＡＣＥＦの面積を求めなさい。

長方形ＡＢＣＤと長方形ＡＣＥＦ、どちらが大きく見えますか？
また、ルート記号は不要です（大ヒントかな？）。

32（平方cm）

ＡＣが長方形ＡＢＣＤの対角線であることから、三角形ＡＣＤ＝４×８÷２＝16（平方cm）とわかります。
ここで、三角形ＡＣＤは長方形ＡＣＥＦの半分であることがわかります。

（長方形ＡＣＥＦ＝ＡＣ×ＡＦ、三角形ＡＣＤ＝底辺ＡＣ×高さＡＦ÷２より）
よって、長方形ＡＣＥＦ＝16（平方cm）×２＝32（平方cm）となります。

解説を見てわかるとおり、なんてことない問題です。

しかし、時間が限られた（しかも入試本番で最高に緊張している）時間で処理しなければならないとしたら…？

まず、ＡＣの長さを求めようとして…、ＡＦの長さに注目して…となってしまうことでしょう。

入試問題には、このように一見簡単に見えるにもかかわらず、即答できず、思考を停止させる「ストッパー」が数多く存在します。
これこそまさに、良問の類といえるでしょう。

　さて、この問題を、見た目と同様に容易に処理するには、次の２点が必要です。
1）与えられた情報（辺の長さ）から、わかることは何か？
2）図形分割における、面積比の基本（←問題演習で身につけられます）

　仮に、この問題が即答できないとしても、長方形ＡＢＣＤと長方形ＡＣＥＦはどちらが大きいか？
くらい、意識して欲しいところです。

灘中より。問題文に明記されていない隠れた条件を使います。

2桁の整数が4つある。この4つの数のうちの2つの和と差を全部調べたら、和のうち最も大きいものは187で、最も小さいものは137であり、差のうちで最も大きいものは40で、最も小さいものは10である。4つの数のうち小さい方から2番目の数を答えよ。　（灘）

偶数と奇数をたすと奇数になります。

54つの2桁の整数を大きい順にＡ、Ｂ、Ｃ、Ｄとします。
問題文の条件は
Ａ+Ｂ＝187
Ｃ+Ｄ＝137
ＡｰＤ＝40
という式で表せます。

ここでＡとＢの和が187という奇数であることから、ＡとＢのいずれかが奇数であることがわかります。
よってＡとＢの差も奇数です。

同様に考えるとＣとＤの差も奇数です。
最小の差というのは、大きい順に並べたときのとなりとの差であるから（例えばＡｰＣが最小になることはない）4つの数のうちの2つの差の組み合わせで10となる候補はＢｰＣのみ。

よって、ＡとＢの差は11以上になるが、和が187でともに2桁の数という制約で考えると、Ａが99でＢが88という組み合わせしかない。
よって2番目に小さい数Ｃは88-10=78

答え78

いくつかの整数の和と差のヒントから元の数を考えるという問題です。

条件の与えられ方や題材（おもり、体重、テストの点）などは表面的に色々なバリエーションがありますが、ポイントは隠れた制限を見つけ出すことです。その主たるものが今回の偶奇と桁数の制限です。これらをつかってＡ+ＤとＢ+Ｃのどちらが大きいのかを判断したり、最大、最初の数を確定させたりします。

偶奇の性質の活用は、非常にシンプルなだけに思考から外れてしまいがちな難しい技術です。

「和や差から元の数を求める」という問題に出会ったときは、必ずチェックする項目として覚えておきたいものです。

「上手な足し算」を設計する力が問われます。

1，2，3，4，5の数字が書かれたカードが1枚ずつあります。これらのカードを使ってつくることのできる5桁の数すべての和を求めなさい。

全部で120通り。足し算をしていくには多すぎます。

5枚のカードを1回ずつ使うので、その並べ方は5×4×3×2×1＝120通りある。
これら120通りの5桁の数の各位を構成する数字に着目する。
120通りの一万の位には1,2,3,4,5が同じ回数ずつ使われている。つまり各数字24回ずつである。
千の位、百の位、十の位、一の位も同様。
つまり、すべての数の和は

（1×24+2×24+3×24+4×24+5×24）×10000+
（1×24+2×24+3×24+4×24+5×24）×1000 +
（1×24+2×24+3×24+4×24+5×24）×100+
（1×24+2×24+3×24+4×24+5×24）×10+
（1×24+2×24+3×24+4×24+5×24）
＝ （1×24+2×24+3×24+4×24+5×24）×11111=3999960
答え：3999960

効率的な数え上げを問う問題はその場での思考力を問わていると思われがちですが、
全く使った経験のない手法をその場で思いつくのはほとんど不可能です。

普段から、様々な問題に取り組み、模範解答で提示されている洗練された手法の仕組みをしっかりと確認していくことで蓄積されていくものです。

多くは、「数字を横ではなく縦に読む」つまり位ごとに整理していくという考えが根底にあるものです。答えがあっていただけで満足せず、様々な別解を探求する姿勢だけがこのような能力を高めることにつながります。

集合の全体を見渡す力が問われます

1001から3139までの数について、数字0が現れない数はいくつありますか。

4人の中から3人を選ぶ選び方と同じ手法ですね

区切って数えていきます。1001から2999を考えます。

1□□□、2□□□を考えたとき、0が現れないということは、□の中に1から9までの数字しかつかわれないということです。

よって1□□□は9×9×9=729通り、2□□□は9×9×9=729通りあるので合わせて1458通り。

3000から3110まではすべて0が使われている。3111から3139までを上と同じように考える。

つまり31□□で□に0を使わないというのは1から9までで構成されているということ。

十の位は1か2か3の3通り、一の位は9通りあるので3×9=27通り。

よって合計1458+27 =1485通り

ヒントの問題はだれもが一度は触れているもののはずです。

ポイントは全体から求めたい集合をのぞいたもの（補集合）を上手く活用するということです。

これは、本問のような場合の数だけでなく、求積問題などでも非常によく使われ、有用な視点です。

(全体から余分なものを求めて引くというもの）どちらに着目しても、答えにたどり着くことは可能なのですが、そこは出題者も意図していて計算量、難易度に大きく差がでるように設計します。

求めたいもの自体を、違った形に変形して求めることは可能か。問題の主旨を損なわずにすり替えることは可能か。という意識は常にもちながら問題に取り組むことが必要です。

「連続する整数」の持つ様々な性質に注目します。

8=3+5
45=13+15+17
45=5+7+9+11+13
のように連続する奇数の和で表すことができる整数があります。495を連続する奇数の和で表す方法をすべて書きなさい。

「連続する数」の扱いには共通の手法があります。

奇数の和が495という奇数になるので、足し算に使う数の個数は奇数となる。
また、連続する奇数個の奇数の和は、平均となる真ん中の奇数×個数で求めることができる。

495=3×3×5×11より、求める奇数の個数は3個、5個、9個、11個、15個、33個、45個・・・など495の約数個を考えればよい。

3個の場合、495÷3=165より真ん中は165となり、3つの奇数は163、165、167となる。

5個の場合、495÷5=99　より真ん中は99となり5つの奇数は95、97、99、101、103となる。

9個の場合、495÷9=55　より真ん中は55となり9つの奇数は47、49、51、53、55、57、59、61、63となる。

11個の場合、495÷11=45より真ん中は45となり11個の奇数は35、37、39、41、43、45、47、49、51、53、55となる。

15個の場合、495÷15=33より真ん中は33となり15個の奇数は19、21、23、25、27、29、31、33、35、37、39、41、43、45、47となる。

33個の場合、495÷33=15より真ん中のは15となるが、15を中心として33個の奇数を並べることはできない。（小さい方向に16個の奇数を並べようとすると0より小さい数が出てきてしまう。）

これ以上の連続する奇数を考えると同様になる。よって答えは、上記に示した5通り。

「連続する整数」の和というのは（最初+最後）×個数÷2という計算手法は有名ですが、その仕組みをしっかりと確認していないと、今回の応用は難しかったのではないでしょうか。
連続する整数の列において、（最初+最後）÷2の意味は平均です。棒グラフにしてみると直感でも理解できるはずです。また連続する数とその和というのは偶奇やその個数など以外と制約が多いことも覚えておきましょう。一見、条件が足りないように見えてもそれらの条件から答えを絞り込むことが可能となります。

麻布中より。倍数判定法の基本が高いレベルで問われます。

Ａは４けたの整数でそれぞれの位は同じ数字からなり、Ｂは４けたの整数でそれぞれの位は2種類の数字からなっています。ＡとＢの積を計算したら44448888になりました。ＡとＢを求めなさい。(麻布中）

「すべての位が同じ数字である整数」を割り切る数のうちの1つは「見た目」で簡単に見つかります。

すべての位の数が同じである4けたの整数Ａは1111の倍数となる。
Ａ＝1111×□となるからA×B=1111×□×Ｂ=44448888であることがわかる。

44448888÷1111=40008であるからＢ×□＝40008となる。

ここで40008＝4×10002であり40008=6×6668であり、 40008= 8×5001であることから、□の候補は6もしくは8となる。
□が6のときＢは6668、8のときは5001となるが、Ｂは2種類の数字のみでつくられる4けたの整数のなので6668となる。
よってＡ＝1111×6＝6666

答え：A＝6666,B=6668

基本的な倍数判定の知識をしっかりと自分のものとして、使いこなせていないとゴールまで簡単にはたどりつけません。

Aの約数1111の発見に関しては初見の問題としては少々難易度が高いですが、一度本問を解いておけば問題ないでしょう。
この問題は1番の（2）つまり素早く終わらせなくてはいけないもので、ポイントは40008が4の倍数であり、6の倍数であり、8の倍数であることの発見です。それぞれの倍数判定法はどの教科書にも載っている基本事項ですが、直接問われてはいない本問のような形式で素早くチェックするには相当量の練習で知識が定着している必要があるでしょう。