学習塾ロジム　今週の1問by 学習塾ロジム

今週は函館・ラサール中より1問です。

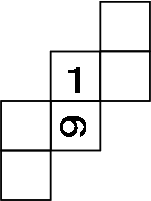
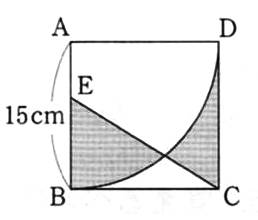
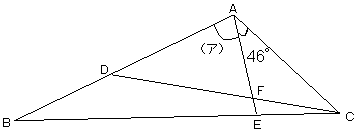
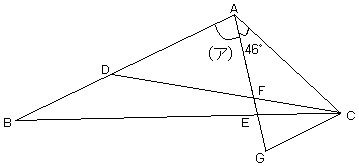
AB=1cm、BC＝1.5cmの三角形ABCにおいて、角 BACの大きさは、角ACBの大きさの2倍です。
この三角形ABCをADを折り目として折るとBとEが重なります。
次の問いに答えなさい。
（１）CDの長さは何cmですか。
（２）ACの長さは何cmですか。
（３）角DECの大きさは角ACBの大きさの何倍ですか。
(函館ラ・サール）

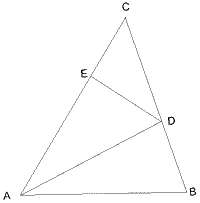
相似の問題です。

「こ の三角形ABCをADを折り目として折るとBとEが重なった」という問題文の設定より、
三角形ADEと三角形ADBは合同なので、角EAB＝角DABとなる。

これと「角CABは角ACBの2倍である」という条件を合わせて考えると、
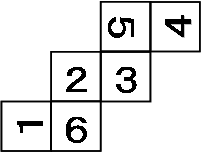
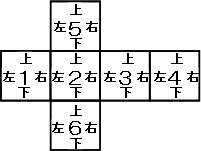
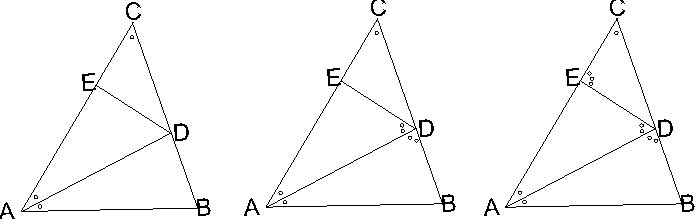
角ACB＝角EAD＝角BADとなる。この角の大きさを下の図に「○」で表すこととする。（図1）

ここで、角ADBは、三角形ADCの外角であることから、角ADB＝角CAD+角ACDとなり、
○×2の大きさとなる。
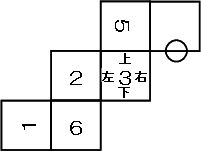
また、折り返したという設定より、角EDAも同じく○×2の大きさとなる。（図2）

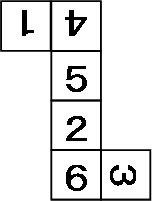
さらに、角EDBは、三角形CEDの外角であることから、角EDB＝角CED+角ACBとなる。
角EDB＝○×4、角ACB＝○×1であるので、角CED＝○×3となる。（図3）

（１）三角形ABCと三角形DBAは、2つの内角が等しいので相似である。
三角形ABCにおいて、AB：BC＝1：1.5であるので、三角形DBAにおいてもDB：BA＝1：1.5である。
BA＝1cmであるから、DB＝1×2/3=2/3cmとなる。
よって、CD＝1.5－2/3＝5/6cmとなる。
（答え）5/6cm

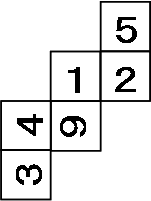
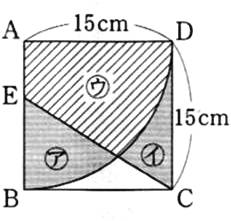
（２）下の図より、三角形ADCはCD＝DAの二等辺三角形である。
よって、（１）よりCD＝DA＝5/6cmとなる。
DA＝5/6を、三角形ABCと三角形DBAの相似の中に当てはめると、
AC＝DA×3/2=5/6×3/2=5/4=1.25 cmとなる。
（答え）1.25cm

（３）下の図より、
（答え）3倍

本問は、解答の下線部である、

「2つの内角が等しいから」相似

という知識を使いこなせるレベルで定着させているかどうかがすべてを握っています。

中学入試ではあまりみかけないタイプの相似で す。
これは、
「2つの三角形が相似となる3つの条件」
をしっかりと頭に入れていなければ気付くことができません。

多くの生徒は、俗に言うピラミッド型と砂時計型の相似にしか気付けません。

そして、「なぜ相似といえるか？」という問い に正確に答えられる生徒も少ないのが現状です。

「相似ならば～」についての練習は数多くこな しているのですが、「～だから相似」については全く見逃されているのが現状です。

合同とあわせて、成立 条件をきちんと整理して、
合同・相似の発見、証明に取組んでおかなければ、
本問のような相似を見つけることは絶対に不可能でしょう。

「雑多な情報の中から、既存のフレームと比較し、適応可能なものを探し出す。

というものがあります。

そもそも「自分が解けるものとは、どのようなものなのか」がわかっていない生徒が、
「自分が解けるもの」を見つけられるはずがありません。

このタイプの問題は、解説を読めば必ず「あ、そうか。」と理解したかのような感覚に陥りがちですが、
問題は「その場で気付けなかった」という事実です。

「なぜ気付けなかったのか。」

それは、往々にして「いま探すべきものについての定義が明確にはわかっていない。」ことが原因なのです。

今週は筑波大附属駒場中学理科より1問です。

種子の発芽に必要な条件を調べるために実験をし、下のような結 果を得た。この実験だけからわかることはどのようなことですか。「種子の発芽には、」に続けて、発芽に必要な条件を説明する文を書きなさい。

[実験１]　シャーレに水を1cmの深さに入れ、その中にダイズの種子を10個入れ、良く日のあたる机の上に置いた。
[実験2]　シャーレに水を1cmの深さに入れ、その中にダイズの種子を10個入れ、ポンプで空気を送りながら、よく日のあたる机の上に置いた。
[実験3]　シャーレに水を1cmの深さに入れ、その中にアサガオの種子を10個入れ、ポンプで空気を送りながら、光が当たらないように大きな箱をかぶ せ、実験1,2と同じ机の上に置いた。

（実験結果）
実験1：種子はひとつも発芽しなかった。
実験2：すべての種子が発芽した。
実験3：すべての種子が発芽した。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（筑波大駒場中）

ロジム生にとってははおなじみの質問ですが、「比べること」とは結局なんでしょうか。「同じことと違うことを見つけること」です。比べる対象同士の差と、その差の数に注目しましょう。

「種子の発芽には、空気が必要となる。」

この解答で、「光が必要ない」と書いた場合、それは不正解です。

また、「空気が必要で、光は必要ない」と書いた場合も部分点なしの不正解となって然るべきです。
光が必要ないと書いた瞬間にゼロ点となるべきだと思ってください。

なぜなら対照実験の意味がわかってないということになるからです。
（声の教育社発行の過去問では解答に「光が必要ない」とありますが、
とんでもない誤答です。気をつけてください。）

ヒントにも書きましたが、「比べる」とはどういうことでしょうか。
「物事の同じことと似ていることを見つける」ことです。

この問題は典型的な対照実験ですが、
上記の「比べること」の意味がわかっていないとしっかり減点される仕組みになっている、
まさに「うなりたくなるほどの」良問です。

実験1・2・3の「差」に注目しましょう。

実験1と2の差は「空気の有無」です。そして結果に1つの違いが生まれています。
つまり、この１つの結果の原因が、この「差」にあたるのです。

つぎに、
実験2と3を比べます。両者の差は、「ダイズなのかアサガオなのか」と、「光の有無」です。
つまり、差（ちがうところ）が2つあるのです。
差が2つあって、結果がひとつ。
結果の原因となる「差」が一つに特定できないことに気づいてください。

つまり、対照実験とは、「１つ」の差違を特定するという作業です。

差違が二つあれば、どちらの差が、結果を生み出しているのかだれもわかりません。

まわりくどいい方ですが、例えばこの場合、
「ダイズの発芽に光が必要かどうかはわからない」のです。
たまたま、アサガオが日光のないところで発芽できる種類かもしれなく、
その真義の確認はこの三つの実験からはわかりません。

実際の試験では、多くの受験生が、
「種子の発芽には空気が必要で、日光は必要ない」という解答をし、
ゼロ点となっていったと予想できます。
もう一度、対照実験とは、そして「比べるとは」という基礎技術の復習をしてみてください。

～今回の問題から導かれる出題校からのメッセージ～
・　自分の常識にしばられないことが重要
・　基礎的な実験・思考方法を根本からわかっていることが重要

どの教科書にも「種子の発芽に光は必要ない」と書いてあります。
筑波大駒場志望の生徒なら絶対知っている知識です。

しかし、この問題は、あくまで「この実験からわかることを」と明記してあり、
「既知のこと、常識とされていること」に関わらず、
対象から「論理的」に結論を導く能力を厳密に確認しているわけです。

常識や知識は、あくまで思考の土台です。
そこに胡坐（アグラ）をかいたままの生徒は必要とされていないのです。

また、ここでいう論理的とは、「比べる」能力です。
そして、比べる能力とは、物事の類似点と差異を明らかにする能力のことです。

そもそも対照実験とはなんなのか、

「1つの差」をみつけ、１つの「結果」に結びつけること

だと理解できているでしょうか。
対照実験のような基本的な思考方法について、もう一度、
「そもそもどういう考え方なのか」と自問してみてください。

今週は高知学芸中学より1問です。

下の（あ）～ （え）は同じ立方体の展開図です。（い）（う）（え）の展開図に残りの数字を、向きに注意して書き入れ、展開図を完成させなさい。（高知学芸中）
（あ）
（い）
（う）
（え）

方向感覚が狂わないように、工夫してみましょう。

（い）
（う）
（え）

（あ） のように、上下左右をきちんと記入します。
（い）で考えるときには、○の部分は明らかに3の右と一致します。
（あ）では、3の右と接しているのは4の左なので、方向が確定します。
このように、立体図形や平面図形の移動、折りたたみの問題において、
方向を常に正しく把握するためには、丁寧な作業が重要です。
（あ）
（い）
万が一にも間違えたくはない問題、しかも確認が難しいタイプの問題では、
このような面倒でも確実な工夫が、見直しを含めると一番の近道になるのです。

～今回の問題から導かれる出題校からのメッセージ～
・ 確実性を担保する視点を見つける能力が重要

「見直しをする力」これは、注意力などケアレスミスをなくすための能力にとどまらず、
「その観点から計算してみても成立していれば答えに誤りはない」
という自らの解法とは別の観点を見つける能力のことです。

確実なものは何か、不確実なものは何か。

そして、その不確実性はどの観点からの確認で払拭されるものなのか。

見直しは、自らの計算の足跡をなぞるものではありません。

考え得る様々な視点で検証する姿勢こそが、
未知の分野を切り開く人間に必要な能力なのです。

100％確実なものと、99％以下のものをきちんと見分ける。
100％確実なものを根拠とする姿勢を身につける。

「センス」「ひらめき」による筋道を、確実なものとする論理性。

レベルの高い学校ほど、「柔軟な発想による方針策定」と
「地道な検証」の両方を必要とする問題を出題してきます。

今週は慶應中等部より1問です。

下の図のように、1辺が15cmの正方形ABCDとおうぎ形ABDがあります。点Eは、辺AB上にあり、色のついた2つの部分の面積は等しくなっています。このとき、AEの長さを求めなさい。
円周率は3.14とします。

　（慶應中等部） 　

「明らかに測定不可能な面積の差について 考える問題」といえば。。。

下の 図のように3つの部分を（ア）、（イ）、（ウ）とおきます。

（ア）＝（イ）なので、それぞれに（ウ）をたして、
（ア）＋（ウ）＝（イ）＋（ウ）も成立します。
（ア）＋（ウ）の面積は、半径15cmの円の4分の1なので
15×15×3.14÷4＝176.625
となり、これが（イ）＋（ウ）である台形AECDの面積となる。
よって
（AE＋15）×15÷2＝176.625
という式が成立し、これをとくと
AE＝8.55cmとなる。

答え　8． 55cm

平面図形内での、面積の差、和についての問題 です。

しっかりとした基礎演習をもとに、

「二つのぬられた面積の測定は無理である。」
「三角形EBCの辺EBを導き出すのは無理である。」

という決断をできる かどうかが大切です。

また、和の問題、差の問題では実数が求まることはほとんどありません。
この点に着目すると、方針の選択肢はせばまり ます。

同様の問題（正方形の中に直角三角形が向かい 合って入っているもの）
に4年生で出会っているはずです。
その問題をきちんと抽象化しておけるかどうか が分かれ目でした。

～今回の問題から導かれる出題校からのメッセージ～
・基本問題の整理能力を鍛えよう

基本問題を応用力を持たせるかたちで整理できているかどうかが問われています。

首都圏上位校の中では、 女子学院とならんで算数が基本問題の高い処理能力をもとめる形式となっている慶應中等部ですが、単純な繰り返しだけでは、対応できません。

基本問題＝簡単な問題ではありません。

その先に、多様な応用問題が考えられる土台となる考え方が含まれている問題が
ここで問われる”基 本問題”なのです。

なぜ、基本問題といわれるのか。
その裏に隠されたとても大切な考え方は何か。
そして他分野ではどのように使われているのかなど、
反射的に解けるだけ ではなく、自ら情報を判断し、整理する力が問われています。

じっくり取り組ませる問題の多い他の上位校に比べれば、
「算数が不得意でもなんとかなる」ということはありません。

ハイレベルな受験生の中では、すぐに差がつき ます。
灘中1日目なども同様ですが、
基本問題の基本たる所以をしっかりと考え、
噛締めていくべきだというメッセージが込められた良問です。

今週は桜蔭中理科より1問です。

ものを燃やすとき、空気中の気体がどのような役割をもっているかを調べるために、いくつかの実験を行いました。以下の問いに答えなさい。

[実験1]　
集気びんAの中に火のついたろうそくを入れ、ふたをしておいたところ、しばらくして火は消えた。びんの内側はくもっていた。
[実験2]　
[実験1]の直後、集気びんAの中に、再び火のついたろうそくを入れてふたをしたところ、ろうそくの火はすぐに消えた。
[実験3]　
新しい集気びんBを用意し、その中に火のついたスチールウールを入れ、ふたをしておいたところ、しばらくして火は消えた。びんの内側はくもらなかった。
[実験4]　
[実験3]の直後、集気びんBの中に火のついたろうそくを入れてふたをしたところ、ろうそくの火はすぐに消えた。

問1　実験1,2の結果からわかることを2つ選びなさい。
ア.　ろうそくを燃やすために、酸素が使われた。
イ.　空気中には、ろうそくを燃やすはたらきのある気体がある。
ウ.　ろうそくを燃やした後の気体では、ろうそくを燃やすはたらきのある気体が減少している
エ.　ろうそくの火が消えたのは、集気びんAの中に水ができたためである。
オ.　ろうそくが燃えた後には、二酸化炭素が発生する。

問2　実験3,4の結果からわかることを2つ選びなさい。
ア.　スチールウールを燃やすために、酸素が使われた。
イ.　空気中には、スチールウールを燃やすはたらきのある気体がある。
ウ.　スチールウールを燃やした後の気体では、ろうそくを燃やすはたらきのある気体が減少している
エ.　ろうそくの火が消えたのは、集気びんBの中に水ができたためである。
オ.　スチールウールが燃えた後には、二酸化炭素が発生する。
（桜蔭中）

選んだ「結果からわかること」について、「なんでそれがわかるかっていうと・・・」と自分で自分に説明しなおしてみてください。

問1　イ・ウ
問2　イ・ウ

ポイントは、聞かれているのが「結果からわかること」であっ て、「事実」や「あなたが知っていること」、「教科書にのっていること」を問うているのではないというところです。

問1で見てみると、
ア.　
実験1,2から、ろうそくを燃やすのに「酸素」が使われたことがわかりますか？
わからないはずです。
------------------------------------------------------------------------
例えば、「夜眠る前に、暖かい牛乳を飲むとリラックスしてぐっすり眠れる人が多い」
という実験結果があるとします。
この実験から、「あ、暖かい牛乳には人をリラックスさせる効果はあんだな」とわかりますが、
その原因が、「トリプトファン」という物質だと、この実験結果からはわからないはずです。
それと同じです。
------------------------------------------------------------------------
イ.　
実験1でろうそくが空気中で燃えています。
空気中にはろうそくを燃やすはたらきをもつ気体がありそうです。

ウ.　
実験2でろうそくがすぐ消えたのは、
ろうそくを燃やすはたらきのある気体が減った（なくなった）からです。

エ.　
「火が消える。すると、水が発生する」　からといって、
「水が発生する。すると、火が消える。」とはいえません。
典型的な「逆は真でない」という意識を試す選択肢です。

「カレーを食べると体があたたまる。」からといって、「体がポカポカしているときに、
「あ、これはカレーを食べたからだ！」とは言えません。

オ.　アと同様ですが、実験1,2には二酸化炭素という名前気体の存在をなにも教えていません。

問2も同様です。

～今 回の問題から導かれる出題校からのメッセージ～
・物事の因果関係に敏感になってほしい。

物事の原因があり、結果がある。
この原因と結果は普段、「だから」や「なぜなら」でつながれるのですが、
往々にして、この関係がねじれたり、無関係であったりするものです。
大人である我々でも多分に心当たりがあることではないでしょうか。

この実験結果がある。だから、こういうことが言える。
こういうことが言える。なぜなら、こういう実験結果だから。

自分が出した結論が本当に与えられた前提から言えることなのか。
普段から、「だから」「なぜなら」に敏感になり、
接続語を数式の記号と同等の感覚でとらえることができる生徒に
桜蔭中は門戸を開いているのです。

重宝されることの多い「ロジカルであること」。「ロジカルである」とはどういうことなのでしょうか。
大胆に言い切ってしまえば、
「話がつながっていること」「話の因果関係がつながっていること」なのです。

「話がつながっている」ことで話の説得力は高まります。
そして話をつなげるのが、「だから」や「なぜなら」等の接続語です。

この問題から「常識にしばられてはいけない」というメッセージを読み取るだけではもったいないというものです。
普段から、「だから」「なぜなら」に敏感になってください。

今週は桜蔭中理科より1問です。

　地球上に存在する水の重さの97％が海水です。その他の2%が南極大陸やグリーンランドの氷河、１%が北極海の氷山や地下水などであると考えられていま す。南極大陸やグリーンランドの氷河だけがすべて海水となると、関東地方のかなりの部分は完全に海水面の下になると予想できます。このとき海水面の高さは およそ何メートル上昇（じょうしょう）しますか。
　答えは四捨五入して整数で答えなさい。ただし、海水面の上昇により陸地の面積は変わらず、また水温の変化などによる水の体積変化もないものとします。必 要があれば下の数値をしようしなさい。

地球の表面積全体に対する陸地の割合　：29パーセント
海の平均の深さ　：3800メートル
地球の半径　：6400キロメートル
（桜蔭中）

物事をいかにシンプル化できるか、モデル化で きるか、です。
「必要あれば」とあるとき大抵ヒントの数値は使うものですが、本問では・・・

78　メートル

問題文には（水⇔氷）の体積変化を無視するとあるので、南極の氷すべてが溶けると、地球上の水が２％分増加することになる。

（もとからある海水の体積）：（増加した海水の体積）
＝97　：　2
＝（もとからある海の深さ）：（増加した海面の高さ）
＝（3800メートル）：　？

よって、？＝　3800　/　97　×2　＝78.35・・・

答え　78 　メートル

球の表面積・体積を習っていないのですから、球で考え始めたらアウトです。
（仮に大人が、球で考え始めても海面と陸地の標高差の条件がないのでドツボにはまります）

では、どうするのでしょうか。

地球を直方体のシンプルなモデルとして考えます。
（「そんなの思いつかない」と思うかもしれないでしょうが、球を書いてみたり、円を書いてみたりして試行錯誤を続ければ行き着くはずです。）

上図の　？　が求めたい、海水面の上昇分です。
問題文には（水⇔氷）の体積変化を無視するとあるので、南極の氷すべてが溶けると、地球上の水が２％分増加することになる。

（もとからある海水の体積）：（増加した海水の体積）
＝97　：　2
＝（もとからある海の深さ）：（増加した海面の高さ）
＝（3800メートル）：　？

よって、？＝　3800　/　97　×2　＝78.35・・・

答え　78 　メートル

「南極の氷がすべてとけると、海面が約70メートルあがる」と言うのは、有名な話です。
（ためしに、「南極の氷」　「溶ける」　「海面」　といったキーワードで検索してみてください）

～今回の問題から導かれる出題校からのメッセージ～
・複雑な事象を、シンプルに考えることができますか？
・手持ちの知識をつかって数段階におよぶ思考を展開できますか？

解説にも書きましたが大人がこの問題にトライすると、大抵、球の断面図の絵を書き、
4πr２乗等の表面積の公式をいじくり、途中で挫折します。また、与えられた数式を
いじっているうちにそれらしい答えがでることもありません。

物事をシンプルに考えられますか。複雑な物事を、シンプルなモデルとして捉えられますか。
これが今回桜蔭が投げかけているメッセージです。

そして、「シンプルに考える」というのは、一朝一夕にできる能力ではありません。

答えまでの作業マップを絶えず頭に描いては修正していく必要がある問題が桜蔭では頻出です。
目の前の数字や数式をいじくり答えにたどり着くことはありません。答えを求めるために求めなくては
いけないもの、さらにその求めなくてはいけないものを求めるために、必要なものはなにか、
絶えず数歩先を見ながら処理を行う能力が必要なのです。
その処理を繰り返した先に本問のようなシンプルなモデル化があるのです。

いくつもの模式図をかき、自分ができること、できないことを考えた末に上のような直方体の
モデルにたどり着くのです。そして桜蔭中学が求めているのが、まさにそういった経験をつんでいる生徒なのです。

「考えに考えて、結局シンプルなモデルにたどり着く」科学者が得る喜びとは、
こういったものなのかもしれません。

今週は東邦大学付属中東邦より1問です。

下の図のように左から順に正方形をならべ、各頂点を結んでいきます。この直線（対角線）について次の問いに答えなさい。
（１）4枚目をならべると、3枚ならべたときよりも直線は何本増えますか。
（２）7枚ならべると、直線は全部で何本になりますか。
（３）直線が150本を越えるには、少なくとも何枚の正方形が必要ですか。

（東邦大学付属中東邦）

(2)までの結果をしっかりと考察してみましょう。

正方形の枚数と直線の本数を表にしてみると下のようになる。

正方形の枚数がｎ枚のとき、直線の本数は
n×(n+1)　本
となっています。

(1)表より、
20-12=8
答え 8本

(2)上記の式において、nが7の場合を考えると
7×(7+1)＝56　　
答え 56本　

(3)
nが11の場合　　
11×(11+1)=132
nが12の場合
12×(12+1)=156
よって
答え12枚

見抜く力と同時に、
・すばやく整理し規則性の発見のための考察
・検討に時間を割くという思考プロセス
が身についているかどうかが勝負の分かれ目です。

そもそも理系志向の強い生徒が集まる学校です。
こういった問題に、粘り強く取り組む姿勢は身につけておいてほしいものです。

本問のように、規則性を見たことのない式で表さなくてはいけない問題は近年頻出です。
「nを使っ た式であらわせ」という出題もかなり見られるようになりました。

まず多くの漸化式タイプの問題に当たっておくことが大切です。
規則性のパターンは、高校生でも手を焼くぐらい様々なものが考えられます。

少なくとも典型パターンだけは頭に入れておいたほうが良いでしょう。
「漸化式を作る」という意識付けもとても大切な要素です。

合格最低点という考え方では、（１）と（２）でどうにかなるものですが、
普段の思考トレーニングとしてしっかりと取り組んでおきたいタイプの問題です。

きちんと表にしたり、「見やすい形に整理する」ことは、「気付き」が重要となる本問においてはとても大切なものです。論 理の積み上げだけでなく、「見やす くすることで、ある突破口に気付く」というアプローチは、中学受験においてとても大切な身につけておいて欲しいものです。

～今回の問題から導かれる出題校からのメッセージ～
・初見の事象に対し粘り強く考察する力が大切です。

理系教育に力を入れていると公言する東邦大学附属東邦中学校。
その言葉通り、理科系研究において最も基本的な能力である「粘りづよい考察力」を問う良 問です。

（１）と（２）は、丁寧に見やすく（この作業の正確さも、理系として必須の能力ですね。）書き込んでいけば全く問題ありません。
（３）が問題です。
1枚目～7枚目まで（鋭い生徒は4枚目まで）の結果を元に、法則を見つけ出さなくてはいけません。

本問は図形の範囲ではなく、数の規則性、数列で言う漸化式の問題です。
ｆ(n)=n×(n+1)を導き出すのは、そう容易いことではありません。
（もちろん、nというパラメーターの概念がなくても、□や？等と置くなど、小学校中学年の生徒でも
回答可能です。）
そもそも図形が前面に押し出されていること、そして図形内の直線の複雑さにかなりの受験生が圧倒され、とばしてしまいがちです。

（１）と（２）の誘導により、かなり易しくなっています。（１）、（２）で、書き出し可能な範囲の問題により誘導し、（３）で何百番目というような、規則 性を活用しなくては対応できない問題を出すというのは典型的な流れです。
試験当日はともかく、折角の受験勉強の過程においては、このような実験考察問題に時間をかけて取り組んでいくことは貴重な体験となるのではないでしょう か。

今週は雙葉中入試より1問です。

太郎さんはA町から一本杉を通って山頂Bまで登るのに１時間２０分、山頂Bから一本杉を通ってA町まで下るのに５５分かかります。ある時A町から山頂のB まで登るのに、一本杉と山頂のちょうど真ん中の地点で忘れ物に気が付きすぐ町までもどりました。そして忘れ物をとり、すぐ山頂へと向かい、はじめに町を出 発してから３時間５分後に山頂に着きました。もしも一本杉で忘れ物に気づいていたら、かかった時間はいくらだったでしょうか。太郎さんは登るときと下ると きはそれぞれ決まった速さで歩きます。

（雙葉中）

求めたい部分の距離の比を明らかにしてくれる ものは、時間の比しかなさそうです。

わすれものに気付いた地点をCとして考えます。
かかった時間より距離の比が求まる。

AB往復：80+55＝135分
AC往復：185-80＝105分

よって、AB：AC＝105：135＝7：9となる。

図のように距離の割合を考えると、
CBの割合は
9-7＝2
となり、Aから一本杉までの割合は

9-2×2＝5
となる。

よってA～一本杉間を往復するのにかかる時間は
105×5/7＝75分

求めるべきは「A～一本杉間往復＋A～Bの上り」なので
75＋80＝155分

答え　2時 間35分

速さと比の難問の典型例です。
雙葉中は処理能力だけでなく、かなり深く、丁寧な読み解きを要する問題を出してきましたが、女子校ではかなり重い部類の問題に入るでしょう。

ポイントは、

「求めたい片道の距離の比は、往復の距離の比と同じであり、往復にかかる時間の比から求められる」

という考え方です。

距離、速さの問題は、使う要素が「時間・速さ・距離」の3つしかありません。
この3つが、様々な形で見えにくくされていることが、この分野の難問の典型かつ唯一の方式です。

本問のように、片道の距離の比を求めたいけれども、片道の時間の比は求まらないなど、
求めたい値と同じ意味をもつ値を的確にさがさなくてはいけません。

ただ、よく考えてみると当たり前。
目の前の比の値に引きずられ、数学的に解こうとすると行き詰りますが、頭の中できちんと人が動いているイメージを作るとすぐに気付けます。

「同じ距離を歩いた時間の比」と聞くと、同じ方向に向かって、同じ時刻に並走していることを想像しがちですが、時期が違っても、逆向きに歩いていても良い のです。
「必要な情報」について、要点のみをしっかりと把握することで、視野が広がってきます。　

～今回の問題から導かれる出題校からのメッセージ～
・数式と現実のイメージの結びつけを怠らないこと
算数の基本は、「数え上げ」と「測定」です。
つまり明確な対象がある場合がほとんどです。

「何を求めているのか。」「何を探しているのか。」に関して、
明確なイメージがなければ数えることも、測定することも不可能です。

にもかかわらず、勉強を進めていくと、とくにハイレベル勉強に進むにつれ、
数式のみを操作している時間が増えてきてしまいます。
常に、図式化することで数式だけでは表せない、
同値変形のヒントや言い換えのヒントを探るという、
算数を学ぶことの意味をきちんと教えてくれる良問です。

今週は桜蔭中入試・理科より1問です。

　温暖 化による海水面の上昇（じょうしょう）は、氷や雪がとけて海水を増加させることがおもな原因となります。北極海の氷山と南極大陸の氷河が、それぞれ同じ重 さとけた場合、海水面の上昇に与える影響（えいきょう）はどのようにちがいますか。つぎのア～ウから選びなさい。

ア.　北極海の氷山による影響（えいきょう）が大きい
イ.　南極大陸の氷河による影響が大きい
ウ.　同じ量ならば、変わらない　　　　　　　　　　　　　　　　　　　　　　　

（桜蔭中）

まず、北極海の氷山と、南極大陸の氷河の違いはなんでしょうか。

答え.　イ

北極海の氷山がとけても海水の深さは変わらない　

ヒントにも書きましたが、
・北極海の氷山
・南極大陸の氷河
の2者の違いはなんでしょうか。

氷が水面に浮かんでいるのか、地上にのっているのかです。

これに気付いた時点で、基礎学習を積み重ねている生徒なら即答できたはずです。

「コップの中に氷が浮いています。この氷がすべてとけると、コップの中の水面はどうなりますか」
という有名な問題を思い出してください。思い出せなくても、考えてみてください。

水は凍る際、体積が増えます。もちろん重さは変わりません。
氷全体の重さと、水面下の氷の体積×1.0ｇ　がつり合っています。
なので、水面上に出ている氷の体積が、水が凍る際に増えた分の体積になります。よね。
（上記3行の詳細解説は省略します。どの参考書を見ても載っているはずですので、
分からなかったら確認してください）

つまり、コップの氷がとけても、水面の高さは増えません。水面は高さ変わりません。

北極の氷山は、コップの氷と同様に考えられます。
とけても海水面の高さは変わりません。

南極大陸上の氷河は、水面に浮いていた氷と違い、
氷（水）の体積はもともと、海水の体積とはカウントされていないため、とけた分はそのまま
海水の増分となります。　

～今回の問題から導かれる出題校からのメッセージ～
・未知の問題を、身近な出来事・既知の問題に置き換えることが重要
ロジムの講義でも、またこの「今週の1問」でもお馴染みの科白です。
あまりにおなじみ過ぎて、「またですか・・・」という声が聞こえてきそうですが、

それだけ多くの中学で問われる重要事項であり、
それだけ多くの小学生が苦手とする能力だと断言できます。
（小学生に限らず、むしろ中学生、高校生、大学生、社会人になっても「優秀」と呼ばれるかどうかのファクターとな る能力なのではないでしょうか）

はじめて見た問題を、「知らない」「忘れた」「習ってない」では何も進みません。
この問題をみて「南極？北極？え、習ってないよ」という発言をするようでは先はありません。

南極大陸の氷河と北極の氷山の違いをまず洗い出し、その違いから、
既知の知識につなげる（本問では、コップ中の氷の問題）。

未知の問題・困難に遭遇し、既知のパーツを集め、解決に向かう。
「受験を通り越して、真に問題解決力を持つ生徒を育てたい」
という名門桜蔭中学からのメッセージを読みとれる1問です。

今週は灘中入試より1問です。

下の図 で、ACの長さは10cm、AFの長さは6cmです。
（辺ADの長さ）：（辺BDの長さ）＝3　：　2
（辺BEの長さ）：（辺ECの長さ）＝5　：　2
とするとき、図の角（ア）の大きさを求めなさい。

（灘中）

「角アを求める」はどこから手をつけていいのかわかりませんよね。まず、手持ちの選択肢を冷静に洗い出して みましょう。

下の図のように辺ABと辺CGが平行となるように、AEの延長戦上に点Gをとり、辺EGと辺GCという補助 線を引く。

すると三角形ABEと三角形ECGが相似　(相似比はBE:ECより5:2)　となる。
また三角形ADFと三角形GFCも相似となる。

AD:DB=3:2なので、AD:DB:GC=3:2:2となる。
よって、三角形ADFと三角形GFCの相似比はAD:GC=3:2となる。

以上よりAGの長さは

6×　（3+2）/3　　=10cm

となる。

ここでAC=10cmと問題文にあるので、三角形AGCはAC=AG=10cmの二等辺三角形となる。
錯角を利用し、角（ア）＝角G。
よって角(ア)＝角G=（186－46）÷2＝67度

答え　67 度　

解くための第一歩。それは
「そもそもこの角アなんてどうやっ たら求まるのか？」
としっかり立ち止まって、方針を考えるこ とです。

図形のなかのある角度の大きさが判明するときに必要な要素が
どのようなものなのかを精査してみることが大切です。

三角定規と同じ形の三角形や、正三角形、角度がわかっている二等辺三角形などはここには１つもありません。また３つの内角のうち ２つがわかっているような三角形も１つもありません。

ここまでしっかりと整理、チェックを進めて行くと

「どこかに 合同、相似の図形を見つければ、角アが判明するのではないか 。」

という突破口となる方針にたどり着きます。

～今回の問題から導かれる出題校からのメッセージ～
・出来ること、出来ないことをしっかりと見極める力が大切
本問は、1日目の問題です。
つまり1問あたり3分～５分で解き 進めなくてはいけない問題群の中の1問です。
何も考えずに、辺の比から面積比を求めたりし始めると泥沼です。

そもそも面積比から角度を求めることはとても難しいですし、
そのような問題に出会ったこともないはずです。
「とりあえず～」という浅い考えで動き始めると５分はあっという間です。

情報を精査して方針を決定するというレベルの高い判断力が求められています。

対策は、角 度の練習問題を数多くこなして行く中で、
解法を自分の中でしっかりと整理しておくことです。

そして、問題文を読んだ時に、
自分の考える解法を進める上で 十分な情報があるのか、足りない情報は何か、そしてその足りない情報はどこからか導き出せるのか
という思考回路が動き出すような日頃のトレーニングが大切です。
そうすれば、そもそも情報が足りずに行き詰まることになる解法にはまり込む危険性を回避できるのです。

一つ一つからしっかりと学んで行く問題演習が大切。

こなすこ とが目的になってきた受験生の勉強姿勢に警笛をならす良問です。