|
桜蔭中より。実験データを単なる記号としてではなく意味のある数字としてイメージできないと解けません。

卵の新しさは、食塩水の中に入れて、うくかしずむかで見分けられるということで、つぎの実験をしました。
(1)買ったばかりの卵A、Bと、冷蔵庫の中に長い間入れたままだった卵C、Dを用意しました。
卵AとCの重さはそれぞれ60gで、卵BとDはそれぞれ50gでした。また、卵Aの体積をはかったら55cm3でした。
(2)重さが100gのビ-カーa~eを用意し、それぞれに水を200cm3ずつ入れました。水1cm3の重さは1gです。ビーカーb~eにそれぞれ下の表の重さの食塩を加えてよくかき混ぜて、全部とかしました。食塩水の体積は、下の表のようになりました。
(3)ビーカーa~eに卵A~Dを静かに入れて、卵がうくか、しずむかを調べました。結果は、下の表のようになりました。
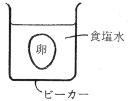
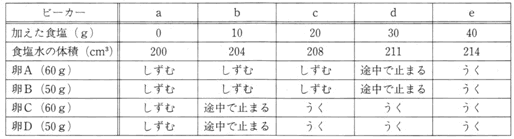
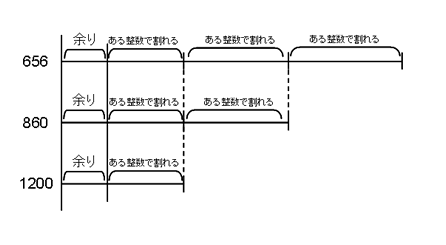
なお、表の中で「途中で止まる」とは、上の図のような状態です。体積1cm3あたりの重さが、食塩水と卵とで等しくなる時に卵は途中で止まります。
つぎの問いに答えなさい。
間1つぎの文の( )~( )にあてはまる数値を下のア~コより1つずつ選んで記号で答えなさい。
ビーカーbの食塩水1cm3の重さは、約( )gになります。卵Cの体積は約( )cm3になります。ビーカーdに卵Aを入れて、上ざら天びんで重さをはかると( )gになります。
ア 0 イ 0.97 ウ 1.03 エ 53.4 オ 55.0 カ 58.3 キ 61.9 ク 335 ケ 390 コ 445
間2 つぎの(1)、(2)の水溶液に卵Aを入れました。卵Aが「うく」ものにはア、「途中で止まる」ものにはイ、「しずむ」ものにはウを記入しなさい。
(1)ビーカーeに、さらに水200cm3を加えてうすめた食塩水。
(2)アルコール50cm3(重さ40g)に、水50cm3を加えた水溶液(体積は97cm3)
間3 この実験の場合、卵の新しさを見分けるのに最も適した食塩水はどれですか。ビーカーの記号で答えなさい。
間4 つぎの(1)、(2)の文について正しいものには○、まちがっているものには×をつけなさい。
(1)適した食塩水を使うと卵の新しさを見分けるのに、卵の重さをはかる必要はない。
(2)同じ重さなら、古い卵は新しい卵より体積が大きい。
(桜蔭中)

実際の試験(当時算数と合わせて55分)では、実際の値を求めて比較する時間はありません。概算力と、それを支える「数字から起きていることをイメージする力」が求められます。

問1 )①ウ ②カ ③ケ
問2 )(1)ウ (2)ウ
問3 ) c
問4 )(1)○ (2)○

問題文を精読し、「浮く・沈む」というのは「1cm3あたりの重さ」の大きさの違いによることを確認します。
問1)
ビーカーbの重さは210g、 体積は204cm3となるので「1cm3あたりの重さ」は 210g/204cm3 となり 1よりわずかに大きい値となります。ここで、210÷204を筆算している生徒は、桜蔭中が必要としない生徒となることでしょう。210/204 が 「だいたい1より少しだけ大きい数」となるというイメージ力を求められています。
卵Cはこの食塩水bと密度が等しいことから、60/? =1.03 ?は60より少しだけ小さい数となる。60と55の差である5の0.03倍は、 0.15にしからない。よって選択肢オの55は除外できる。60÷58.3 と 60÷55などとやっていては試験時間中に解ききれません。
この概算の方法はここでは詳しくはしまぜん。各自「なんとか計算を早くしよう」と拘泥した先に手に入れるテクニックです。各自考えてみてください。
食塩を水にとかしても、食塩の重さは変わらないので、
ビーカーd=卵の重さ + 溶けた食塩の重さ + 水200cm3の重さ + ビーカーの重さ
= 60g + 30g + 200g + 100g = 390g
問2)
(1) 水400cm3、食塩40gを加えた状態となり、これは水200cm3に食塩を20g加えたもの(ビーカーc)と同じ「1cm3あたりの重さ」となります。
(2)アルコールの「1cm3あたりの重さ」は 90g/97cm3 となり 1よりも小さい値。卵Aは重さ60g体積55cm3(問題文より)なので、卵Aの「1cm3あたりの重さ」は1よりも大きく、アルコール中で沈みます。
問3)
「浮き・沈み」の違いが最もはっきり現れるビーカーを選ぶ。
問4)
たまごを「浮くもの」「沈むもの」に分けることができる。cのビーカーに対して、沈むA,Bが買ったばかりのもの、C,Dが冷蔵庫に保管しておいたものであることから、新しい卵は古い卵に比べて「1cm3あたりの重さ」が大きいことが分かる。
~今回の問題より導かれる出題校からのメッセージ~
数字に意味を持たせる姿勢が大切
本文は、十分な時間を与えられれば比較的平易な
計算問題と、実験考察問題です。
合否に影響を与えたのは、短時間にこの問題をとりきる力の有無だと断言できます。
各問題ごとに、それぞれ「1cm3あたりの重さ」の計算をしていたのでは間違いなく時間切れです。
「1より大きい」「1より小さい」
「分母が大きくなれば、全体は小さくなる」
「55の1.03倍はどうやっても60にはとどかない」 等、
概算する能力の有無が求められています。
解説中にも書きましたがこの能力は、一朝一夕には身につきません。
また、1行計算問題集を大量に繰り返しても決して身につきません。
概算力を身につける方法は、唯一、数字を単なる記号でなく、意味のあるかたまりとして
イメージすることです。
例えば、 5.2 / 4.9 を1.06であると計算できることよりも、「1よりも少しだけ大きい数だ」と
イメージできることです。
実際の社会でも、数字の細かい計算よりも、概算によって全体を把握し、判断をしたり方針を立てたりする
能力のほうが遥かに重宝されています。
もちろん正確な計算能力も必要ですが、数式をたんなる記号の羅列としてとらえるだけでは、
計算能力以上のものは身につきません。
(参考)
http://www.lojim.jp/calculation/quiz.cgi







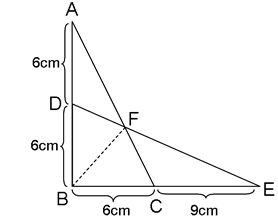

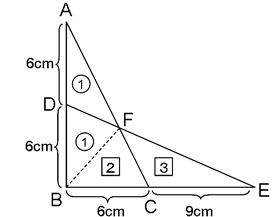
 は=11.25なのでもとめる三角形ABCと三角形DBFの面積の比は
は=11.25なのでもとめる三角形ABCと三角形DBFの面積の比は