|
桜蔭中より。なぜ、教科書から離れ、身の周りの科学を題材にするととたんできなくなってしまうのでしょうか。

自転車は2つの輪じくをチェーンでつないだ道具です。さくらさんは自転車の性質を調べるために次の実験1、2を行いました。それぞれの実験について、以下の問いに答えなさい。
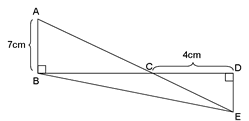
[実験1]さくらさんは、ペダルをおす力と後輪が地面をおす力の関係を調べるために、図4のようなそうちを使って実験を行いました。ペダルにおもりをのせたとき、後輪に伝わる力をばねはかりではかることができます。図4は自転車のペダル、ペダルのじく、チェーン、後輪、後輪のじく、スタンド、軽いひも、定かっ車、ばねはかりを表したものです。
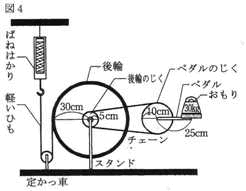
(1)ペダルの長さが25cm、ペダルのじくの半径が10cm、後輪の半径が30cm、後輪のじくの半径が5cmの自転車のペダルに、30kgのおもりをのせました。
図4の状態でつり合ったとき、ばねはかりは何kgをさしますか。ただし、ペダルのじくがチェーンを引く力は後輪のじくにそのまま伝わっているものとします。
(2)この自転車のペダルにのせるおもりはかえずに、後輪がばねはかりを引く力を大きくするには、どのような工夫をしたらよいですか。下のア~クから4つ選びなさい。
ア.ペダルのじくの半径を大きくする
イ.ペダルのじくの半径を小さくする
ウ.後輪のじくの半径を大きくする
エ.後輪のじくの半径を小さくする
オ.後輪の半径を大きくする
カ.後輪の半径を小さくする
キ.ペダルの長さを長くする
ク.ペダルの長さを短くする
[実験2]次に、さくらさんはペダルの回転数と後輪の回転数の関係を調べるために、実験1で使用したばねはかり、定かっ車を取り外し、手でペダルを回し、後輪の回転数を調べました。
(3)さくらさんがペダルを1分間に120回転させると、後輪は1分間に何回転しますか。
(4)ペダルの回転数を(3)のままで、後輪の回転数を上げるには、どのような工夫をしたらよいですか。上の(2)のア~クから2つ選びなさい。
(桜蔭中)

そもそも、滑車やテコってなんのために発明されたのでしょうか。それが分かっていると格段に解きやすいはずです。あとはいつものように、影響を要素に分解して考えます。

(1)
30kg × 25cm/10cm × 5cm/30cm = 12.5 kg
(2)
イ、ウ、カ、キ
(3)
240回転
(4)
ア、エ

テコも綸じくも、結局は重いものを持ち上げるために発明された道具なのです。
その仕組みは簡単に言ってしまえば
「長い距離を動かすかわりに、小さい力ですませる」
というものです。まずこの視点を持つことが大事です。
この視点を持っていないと、テコで、支点に遠いほうの力が大さくなってしまうようなミスに気付かなかったり、
そもそも、この問題のように「日常的に使われてるてこの利用」ということに注意がいきません。
(1)
・ ペダルに重りをのせると、時計回りの回転をつくる力が生じ、チェーンに力が伝わります。その際、テコの原理が働きます。
チェーンに伝わる力は、半径の逆比を考えて(←ここが分からない人は、教科書で勉強するか、塾の先生に聞いてください)
30kg × (25cm/10cm)
・チェーンが時計回りに回ることによって、ばねばかりにつながれたヒモを時計回りにひく。
これも、半径の逆比 を考えて、
(チェーンが引く力) × (5cm/30cm)
⇒30kg × (25cm/10cm) × (5cm/30cm) = 12.5 kg
(2)
(1)より、
ばねばかりの力=(おもりの重さ)×(ペダルのながさ/ペダルじくの半径)×(後輪のじくの半径/後輪の半径)
となる。「結果への影響を構成要素に分解する」 という作業を行う。
上の式をじっとにらむと、
ペダルじくの半径は、大きければ大きいほど、ばねばかりにかかる力を小さくする。
後輪くじの半径は大きくすれば大きくするほど、ばねばかりにかかる力を大きくする。
後輪の半径を大きくすれば大きくするほど、ばねばかりにかかる力は小さくなる。
ペダルながさは、大きくすればするほど、ばねばかりにかかる力を大きくする。
ことがわかる。 これより、イ、ウ、カ、キ が正解となる。
(3)
円周は、半径に比例するから、 回転数は半径の逆比に比例します。
(感覚的にも、大きいじくを回すと、多くのチェーンが巻き取られるのだから、小さいほうのじくは激しくまわりますね)
ペダルのじく(半径10cm)が120回転するのだから、
後輪のじく (半径5cm)は、まず、すくなくとも120回転よりも多く回転することをイメージする。
逆比の分、多く回転するのだから、 240回転となる。
(4)
(3)より
後輪の回転数 : ペダルの回転数 = ペダルじくの半径 : 後輪のじくの半径
⇒ 後輪の回転数=ペダルの回転数 × ペダルじくの半径 ÷ 後輪じくの半径
となり、後輪の回転数を上げるだめには、問題文の条件より、
後輪じくの半径を小さくし、ペダルじくの半径を大きくすればよい。 よって、エ、ア
~今 回の問題から導かれる出題校からのメッセージ~
式処理と日本語での説明をいったりきたりできること
「今週の1問」でよくとりあげる、「現象をいくつかの要素に分解する」という能力が今回ももとめられました。
例えば、今回の回転数をいくつかの要素に分解し、それぞれの項ごとに影響を考えました。
これは実は、とてもとてもとても大事な能力と言われ、時としてこの能力が「優秀さ」そのものとして扱われることすらあります。
大人の世界では、利益を売上と費用に分解したり、
はたまた、とある商品を開発・製造から販売まで何段階にもわけて、そのそれぞれの段階で課題を考えたり、
評価を行ったり(いわゆるバリューチェーンの考え方)ですが、やはり小学生にだって、これがもとめられているわけです。
「複雑な事象を構成要素の分解する」 これこそ、多くの場面で求められる力であるとすれば、
各界で活躍する人材を輩出するいわゆる上位校の入試でこの力が問われるのは当然といえば当然です。
そして本問の注目すべきところは、そういった式をつくるにあたって、絶えず、
「日本語でイメージ」し続ける必要性を教えてくれるところです。やはり良問です。
じくの回転数と半径は逆比になる!なんていうのは、暗記すべきことではなく、問題に当たった際に、
回転する車輪をイメージして式をつくっていくことが必要なのです。
立式や 式への分解が大事だと猛進してしまうと、暗記する範囲が膨大になったり、
ちょっとしたミスに気付かないことがよくあります。とくに、テコ、滑車、浮力、熱量は、式での処理が重要かつ有効でありますが、
式が表す現象をたえずイメージしていないと、途中でなにをやっているのだか分からなくなります。
式への分解以上に、ハイレベルな生徒にとっては、日本語で式の様子をたえずイメージすることが求められるのです。
基礎的な科学を、身の回りに利用に応用した道具の問題が近年、頻出です。
(ボート、スケボー、栓抜き、ペダル、カタパルト、エレベーターetc...)
こういった問題が苦手な生徒は、式や公式が表す現象をイメージできていないのです。
ではどうすればイメージできるようになるのか。。。
それは他の機会ということで。