学習塾ロジム　今週の1問by 学習塾ロジム

思い切った視点の切り替えが求められる問題です。

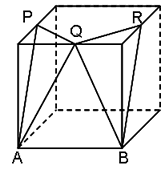
下の図のように４つの長方形と２つの台形からできた容器に水が 入っています。これにさらに水を注ぎ込んだところ、水面の高さは21cm上昇し、水面の面積は252平方センチメートルになりました。
（１）最初の水面の高さは何ｃｍですか。
（２）最初の水面の面積は何平方センチメートルですか。
（３）省略
　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (大阪星光学院中）

「立体図形の問題」だということにとらわれると選択肢が狭まってしまいます。

（１）
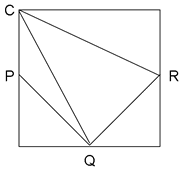
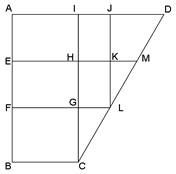
下のように真横から見た形で平面図形として考えます。
alt="" style="height: 188px; width: 234px;">
水を増やす前の水面をFL、注ぎ足したあとの水面をEMとします。

求めるのはFB＝CGの長さです。

EMの長さは、252÷12＝21cm
AI＝EH＝FG＝BC=9cmなので
HMの長さは21－9＝12cm

ここで三角形CIDと三角形CHMの相似を考えると
ID：HM＝（30－9）：12＝7：4
よって
CI：CHも7：4
CI＝84cmなので
CH＝84×4/7＝48cm
GHは、水を注ぎ足したときの水面の上昇分なので問題文より21cm。
よってもとめるべきCGの長さは
48－21＝27cm
答え： 27cm

（２）
求めるべき面積は
FL×12で求めることが出来る。

ここで三角形LKMと三角形CIDの相似を考える。

LK：CI＝21：84＝1：4
よってKM：IDも1：4
ID＝21cmなので
KM＝21×1/4=5.25cm

よってEK＝FL＝EM－KM＝21－5.25＝15.75
故に求めるべき面積は
15.75×12＝189平方センチメートル
答え： 189平方センチメートル

面積を求める問題では、

「目で見て見当をつける」

という作業が大きな重要性を持っています。

相似、合同や二等辺三角形、正三角形の発見は、
大体の見当をつけて、確認作業をするというプロセスで
ほとんどの場合に対応しているといえるでしょう。

本問のように、立体上の面積を求める場合、
与えられる図は多くの場合が斜め上方からの描写になります。

こうして与えられた図形上において、
面積を求めるべき図形は、当然実際とは違った形で描かれます。

そのような状況では、合同や相似の活用など
「目で見て見当をつける」
ことを手がかりに進める解法を発見しづらいのは言うまでもありません。

面倒くさがらずに平面に落とし込む。

その図を見ると、
頭が平面図形モードに切り替わり
「補助線」「合同、相似」などへの感度が高まるのです。

～今 回の問題から導かれる出題校からのメッセージ～
場面に応じて最適な視点に切り替えることが大 事

今週の一問で何度も扱っている「単純なモデルへの変換」という思考技術ですが、

本問は「単純化」という効用だけでなく、

「見慣れた形式へと土俵を移す」

ことに大きな価値があります。

解説にもあるとおり、見たことのある風景の中では
武器を選択する判断力も格段に高まるのです。

初めての問題に対応するとき、
「今までに同じ問題に出会わなかったか」
と考えるパターン認識力をもつことは応用力の第一歩ですが、

単純に同じ問題を探すのではなく問題を分解して
「自分の知っている知識・技術を使える部分はどこか」
という思考でとっかかりをつかむという
高次のパターン認識力を持つことはさらに大きな武器になります。

その場その場で視点を切り替える柔軟性と思い切りの良さが問われる良問です。

武蔵中より。比較説明問題の必勝法をここで得てください。

袋の中に，下の表の(1)～(3)の形をした3つのピンとゴム栓が入っ ています。ゴム栓の平らな面に，それぞれのピンを1つずつ，指で奥まで刺したり扱いたりしてみなさい。刺し方と抜き方について，気づいたことを下の表にま とめなさい。図を用いてはいけません。

(武蔵中）

極端に言えば、「彼の好きなものは、りんごとみかんとイチゴとニンテンドーDSです」という説明に違和感を感じるか、そしてその違和感の原因を理解している かどうかを試されています。

「比べる視点」がそれぞれ刺し方、抜き方でそろっていることがポイントです。
上記解答例では、

刺し方
・真直ぐ指すことができるのか
・どのくらいの力が必要なのか
抜き方
・どのくらいの力が必要なのか

という視点に着目してまとめました。

つい、いろいろ気付いたことを羅列したくなってしまうものですが、
そこをぐっとこらえる忍耐力と、
「この問題は結局、比較の視点についての問題だ」
と判断できる論理的説明問題への慣れも必要ですね。

一 見、何を書いてもよく、そして何を書いていいかよくわからない自由記述のように
思えますが、こういう問題だからこそきちんとした採点基準があってしかるべきなのです。

その基準が「比較の視点がそろっているかどうか」なのです。

（日本語として文章が成立しているか。過不足ない字数を使って説明できるか。
といったことは、本問出題校を受ける受験生ならば最低条件としてクリアしているだろう
ことなのであえてここで言うことではありません。）

この問題のポイントは、

「どれだけ多くのことに気付くことができるか」

ではなく、

「どれだけ工夫して説明できるか」　　

です。

その際に、説明の基本である「比べる視点をそろえる」ということを
今ここで再確認してください。

～今 回の問題から導かれる出題校からのメッセージ～
比べる時は視点をそろえる

他者の説明を読み聞きしているとき、
切り口がそろっていないとその説明はとたん説得力を失います。

わかりにくいからです。

説明をするときは、何を比べるのか、比べるものがそろっているか
ということを徹底的に意識するだけでも、その人の説明力は飛躍的に向上します。

「モレとダブりに注意してものごとを並べる」
ロジカルシンキングの基礎中の基礎ですが、
結局論理的に話したり考えたりすることのエッセンス（本質）がこれなのだと
改めて実感させられた1問でした。

武蔵中より。問題文のヒントを常に頭に置いておく。参照する力が問われます。

AさんとBさんはそれぞれ羊を飼っています。二人とも飼ってい る羊の数は10の倍数です。A、Bの二人とも1日に14頭ずつ羊の毛を刈ると、かかる日数の合計は72日になります。また、19頭ずつ刈るとAの方がBよ り7日早く終わります。A、Bが飼っている羊はそれぞれ何頭ですか。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (武蔵中）

途中で行き詰ったら、本文に戻りましょう。

14 頭ずつで合計72日なので
合計14×72＝1008頭いるともできるが、
最終日は１頭しか刈らなかった場合も考えられるので、
最低14×70＋2＝982頭
であることも考えられる。

この条件より羊の合計頭数は982～1008頭であると考えられる。
ここで、頭数は10の倍数であることを鑑みて、
990頭か1000頭であることがわかる。

次に19頭ずつ刈るとAのほうが7日早く終わるので、差は
最小19×6＋１＝115頭（Aは最終日に19頭刈り、Bは最終日に1頭しか刈らなかった場合）
最大18＋19×7＝151頭（Aは最終日に1頭しか刈らず、Bは最終日も19頭刈った場合）
ここでも、頭数の差は10の倍数であることを鑑みて
差は120か130か140か150頭であることがわかる。

ここで合計頭数と差を使った和差算で合計の頭数を、
結果が10の倍数になるものに限って求めると
（A：B）＝（440：560）（430：570）（430：560）（420：570）
が候補となる。

この中でそれぞれを14で割って、
商＋1の合計が72になる（14頭ずつ刈って合計72日かかる）
のは、（430：570）のみである。

よってA：430頭　B：570頭

答え：A： 430頭　B：570頭

本問の難しさは、解答の進め方にあります。

子供達は、計算式が連なって、最後に答えが出る形式に慣れきっていますし、
答えを取捨選択させるにしても最後の段階に限られているからです。

計算を進める度に、幅が出てしまう。
それを本文の条件に戻って取捨選択し、また進めていくという今回のような形は、
試験中とても不安に思うことでしょう。

最後の答えを、再度問題文に代入することですっきり確認できないこと
（～日で刈り終わる頭数には幅があるからです。）も難しくしています。

このタイプの問題にあたって慣れておくことは大切です。
本文は、この年度の入試の中では、
試験時間内に確信を持って終わらせることが最も難しかった部類に入る問題です。

倍数の制限、偶奇の判断、は答えの幅に大きな制限を加える
隠れた条件となることが多いので常にチェックする習慣をつけたいものです。

～今 回の問題から導かれる出題校からのメッセージ～
式の展開を、与えられた具体的な状況から切り 離してはいけない。

本問のように多くの式を連ねていかなければならない問題では、
いつのまにか本文の内容が頭から離れてしまいがちです。

式はあくまで本文が与えてくれた具体的状況を簡潔に翻訳したものに過ぎません。

行き詰ったときの突破口は、しばしば本文に明記されている条件です。

本文とつかず、はなれず、適度な距離を保ちながら論を進めること。
これは、式の展開の長さが算数の数倍になってくる数学における大切な姿勢です。

本問は、この姿勢の基本部分が身についていることを問う良問です。

慶応普通部より。正確さと大雑把さのバランスが問われます。

次のようにある規則で数が並んでいます。

（１）1段目で左から10番目の数はいくつですか。
（２）32は何段目で左から何番目ですか。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (慶應普通部）

全部書き出せば確実に正解ですが、答えの周辺までざっくり計算することで時間を短縮できます。

（１）
規則は、左下から右上にむけて単調に増加するというものです。
図のように三角形の中に入る数字の個数を考えれば、
「一番左の～段目」や「1段目の～番目」を見つけることができます。

１段目の左から１０番目の数は、
一辺に１０個の数が置かれた直角二等辺三角形に使う数字の数と同じです。
これは１＋２＋３＋・・・・・・＋１０＝５５
答え：５５

（２）
（１）の考え方を使うと１段目の左から９番目は４５、８番目は３６であることがわかる。７番目は２８であるから、３２は、８段目の１番左から始まり１段目 の左から８番目で終わる周期の中にあることがわかる。
８段目の１番左は２９であるから、ここを含め４つ左上にすすんだ５段目の左から４段目が３２となる。
答え：５段 目の左から４番目

規則性のポイントは、迅速性と確実性のバランスをとることです。
最悪すべて書き出せばよいのですが、
それでは時間が足りないような出題構成になっています。

本問でも見つけた規則性を使って

「～段目の一番左はいくつだろう」

という形で一気に進めてしまい、
その結果から微調整していくという姿勢が必要です。

超えても、足りなくてもとりあえず概算をして正答との距離を縮めるという技術は、
単調な計算練習による成果の何倍ものスピードを身につけることになります。

～今 回の問題から導かれる出題校からのメッセージ～
概算によるよい意味での大雑 把な見当づけが大切

上位校の中には、明らかに試験時間に対して問題数の多い
「処理能力が問われる」と呼ばれる試験を行う学校があります。

本校をはじめとして慶応中等部、女子学院、灘などです。

これらの学校の求める「処理能力」とは単純に
ひらめきが速い、計算が速い、字を書くのが速い
といったものではありません。

必要とされているのは、雑多な情報の中から、
重要なポイントにのみ着手する取捨選択の能力です。

「ここまでは大雑把な計算でも間違いなく近づける。ここからは丁寧に。」

という境目をきちんと見つけ出すこ とです。

前者が過剰になれば誤答となり、
後者が過剰になれば時間が足りなくなるのです。

これには、普段からすべてを書き出した場合と、
最短距離をかなえてくれる計算技術を見比べて
その仕組みをしっかりと理解しておくことが大切です。

普段の勉強で～通りを書き出して正解して満足するのではなく、
数の性質の見地から計算で解ける部分を見つけ出すことが大切です。

豊島岡女子・理科より。実験結果分析に関する基礎的な問題です。情報整理・分析・考察という生徒の能力を見事にチェックしています。

アサガオは,夏の早朝に花が聞く植物ですが、なぜ朝に花が開く のでしょう。このような疑問を持った東京に住む豊子さんは次のような実験を行いました。その実験と結果に関する以下の問いに答えなさい。
【実験方法】
　いくつかの鉢を用意してアサガオの種をまき、夏休みに花が咲くように準備しました。8月の初めにつぼみをつけたアサガオの鉢植えを、次のような条件にし て、花が開く時刻を観察しました。

条件1：日の当たる庭（日の出午前4時50分頃、日の 入り午後6時50分頃）に置く。
条件2：外からの光がいっさい入らない部屋の中で電灯 をつけ、ずっと明るい状態にする。
条件3：条件2と同じようにずっと明るい状態にし、6日目の午後4時頃から7日目の午前11時頃まで電灯を消し暗い状態にする。
条件4：条件2と同じようにずっと明るい状態にし、6日目の午後7時頃から7日目の午前11時頃まで電灯を消し暗い状態にする。
条件5：条件2と同じようにずっと明るい状態にし、6日目の午後11時頃から7日目の午前11時頃まで電灯を消し暗い状態にする。
　
【実験結果】
　条件1：日の出時刻とほぼ同時刻に花が開いた。
　条件2：花は開かなかった。
　条件3：7日目の午前2時頃に花が開いた。
　条件4：7日目の午前5時頃に花が開いた。
　条件5：7日目の午前9時頃に花が開いた。

（1）アサガオと同じ時期に花を咲かせる植物を、次のア～オから一つ選び記号で答えなさい。
　ア．アブラナ　　イ．スイセン
　ウ．イネ　　　　エ．アジサイ
　オ．ツツジ

（2）実験結果から、アサガオの花が開く理由はどのように考えられますか。次のア～クから正しいものを一つ選び記号で答えなさい。
　ア．アサガオは、明暗とは関係なく花を開く。
　イ．アサガオは、明るい状態から暗くなって一定時間後に花を開く。
　ウ．アサガオは、暗い状態から明るくなって一定時間後に花を開く。

（3）実験結果から考えて，夏のこの時期、北海道と沖縄ではアサガオの花が開く時刻はどのようになると考えられますか。それぞれについて，次のア～ウから 一つずつ選び記号で答えなさい。
　ア．その地域の日の出時刻とほぼ同時刻に開く。
　イ．その地域の日の出時刻よりも早く開く。
　ウ．その地域の日の出時刻よりも遅く開く。

（4）実験結果から考えて，実験の時期を秋にずらしていくと，アサガオの花が開く時刻はどのようになると考えられますか。次のア～ウから一つ選び記号で答 えなさい。
　ア．その日の日の出時刻とほぼ同時刻に開く。
　イ．その日の日の出時刻よりも早く開く。
　ウ．その日の日の出時刻よりも遅く開く。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (豊島岡女子）

（3） が考察できるかどうかが分かれ目です。東京、沖縄、北海道で異なるものはなんでしょうか。　また、（3）の選択肢中の「その地域」とは東京のことではない ことに注意です。読み違えると解答できません。

（1） ウ　（2）イ　（3）北海道・・・　ウ　　沖縄・・・　イ　(4)イ

（2）おそらく下のような図を（簡単にでもいいので）
問題文を読みながら書けるかどうかが分かれ目です。

条件１： --04：50＝＝＝＝＝＝18：50---------------04： 50＝＝＝＝＝＝＝＝
条件２：　＝04：50＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝04：50＝＝＝＝＝＝＝＝
条件３：　＝04：50＝＝＝16：00-----------02：00----04：50--------11：00＝＝
条件４：　＝04：50＝＝＝＝＝＝＝19：00--------------05：00------11：00＝＝
条件５：　＝04：50＝＝＝＝＝＝＝＝23：00----------------09：00--11：00＝＝

（　--　は夜　　　＝＝　は光を当てている時間　　下線付き赤字は 花が咲いた時刻　）

ここで
・面倒くさがって図を書かない生徒
・国語力不足から、そもそも実験内容を読み取ることができない生徒
の多くはここで撃沈します。

ここで
「夜になってから10時間後に開花する」
または、
「夜が10時間続くと開花する」
ということがわかります。　
（上記のどちらが正しいかは、(3)を解いている途中で気付きます）

それでは、「夜になって10時間後に開花もしくは、夜が 10時間続いたら開花」
　にどうやって気付けばいいのでしょうか。　
「よくみなさい」「よく考えなさい」と言いたくなりますが、
これは助言として成立していませんね。悪い教師の台詞です。

まず
条件２と、条件１から5の相違点を探します。
→花が咲くには夜が必要。
つぎに
条件1、3、4、5　の共通点を探します

このように情報から何かを判断するときは、「相違点」「共通点」に着目して考えます。

普段から小学生の皆さんも自然と行っている行為ではありますが、
情報整理のフレームとして認識している小学生は少ないのではないでしょうか。

結果考察でどうしていいかまったく分からなくなったら、とにかく
「違うところ（相違点）」「同じところ（共通点）」を列挙してみてください。

（3）
選択肢の「その地域」が東京ではなく、それぞれ北海道と沖縄であることを
きちんと把握してください。これを勘違いすると解けません。
（教室ではここを勘違いしての誤答が多数ありました）

東京と、沖縄・北海道で何が違うのかに着目します。
経度・緯度がそれぞれ違いますね。

◎経度の違い　
→　北海道は東京より東　　沖縄は東京より西　→

北海道：　日の出　４：50以前　　日の入　16時50分以前
沖縄：　日の出　4：50以後　日の入　16時50分以前

となります。
東京の日の出に対しては、10時間の夜が明ける（＝花が咲く）時間はずれますが、
それぞれ、北海道、沖縄の日の出時刻に花が咲くことには変わりません
（選択肢をよく見てください）
なので経度による違いは考えません

◎緯度の違い
→北海道は東京より北　沖縄は東京より西　→

夏の北半球では、緯度が大きくなるほど（＝北に行くほど）、夜の時間に対して昼の時間は長くなる。
（下図参照）

よって、北海道では、東京よりも昼が長く、夜が10時間以下になります。
（解答の選択肢に「咲かない」というものがないため、ここで、
「開花は、夜が10時間続くと起きる、
ではなく、夜になってから10時間後に起きるのだ」
ということに気付きます。）
なので、開花は、夜になってから10時間後つまり日の出後に起きます。

同様に沖縄では日の出前に夜になってから10時間後を迎えます。

(4)は　（3）が分かる生徒は100％解答できるはずです。（3）をあてずっぽで正解した
生徒と、理解して正解した生徒の得点差をつけるために設置されているのがこの（4）だと
思ってください。　

～今 回の問題から導かれる出題校からのメッセージ～
差（=違い）を網羅的に把握することへの意識をもつ

教 室でこの問題をやった際には、
（3）で経度による差のみを考え、混乱する生徒が多数いました。
地球上の２地点の差異を考えるのに、緯度による差に気付かなかったのです。

(1)でのアサガオが開花する条件探しにおいても必要な能力となるのが、この

「差違を網羅的に並べる」　　です。

我々が物事を判断するとき、大概の場合において何かと何かを比較しています。
比較が判断を生んでいるのです。
そしてその比較こそ、「差違を考える」行為なのです。

なにか判断に困ったときには、
「両者の差はなんだろう」
「両者の差はこれだけで十分なのか」
と強く意識してみてください。

慶応 普通部より。数を整理する力を測定します。

3を1以上の整数の和で表すと1＋2、1＋1＋1の2通りになります。5をおなじように1以上の整数の和で表す方法は何通りありますか。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (慶應普通部）

こういった数え上げのポイントは、最も大きな数を固定して整 理することです。

以 下の表の６通り

正確に数え上げるポイントは、
「間違えにくい手法で数える」ことに尽きます。

今回でいえば、1+4,2+3,1+1+3,1+2+2,・・・・
といった書き出し方は間違いやすいものです。

「500円を１00円玉と50円玉と10円玉で支払う支払い方は何通り？」

といったタイプのものが代表的ですが、
何か１つのもの（大きなものが一般的です）を固定して、
残りを考えるという手法は一度経験しておくべきです。

また、50円玉が1つ減れば、
10円は5枚増えるというそれぞれの数の関係を
しっかりととらえることも数え間違いや数え忘れを避けるには有効です。

本問は、普通部の問題としては標準です。
受験生のレベルを考えればかなり簡易な問題で
間違える生徒は皆無といえる問題です。

上記のような数え上げの意識を確認するということに加え、
次のような面白い問題の元となるので取り上げ問１
9を3以下の整数の和で表す方法は何通りありますか。

問2
12を1＋1＋10のように3つの整数の和で表す方法は何通りありますか。

ともに大学入試での超有名問題ですが、
小学生でも正答率はほとんど変わらないでしょう。
ともに答えは12通りです。
まずは間違えずに書き出すことに注力してみましょう。
12通り書き出せたらまず合格です。

この問題の面白いところ、
それはこの2つの問題の答えは必然的に同じになっているのです。
その理由を考えて見ましょう。

～今 回の問題から導かれる出題校からのメッセージ～
数を整理する力が大切

数 をその場で必要な形で整理する能力は、
数の規則性、対称性などに対する感覚を必要とするものです。

九九の表や、倍数・約数の関係など数多くの問題に触れ、
答えを探し出すだけでなく、
数の性質に絡めてなぜそのような手法で答えをだすことができるのか
について考えてみる習慣をつけておきましょう。

パスカルの三角形などわかりやすいものを取っ掛かりに、
小学生の算数の中でもっとも奥深い「数の性質」に興味を持ち、
掘り下げる視点をもつことが良いかもしれません。

栄光学園中より。他者への説明とは何なのか。真っ当な論理性を問う良問です。

下の図の8つの空欄に、それぞれ異なるように整数を1つずつ入れていきます。このとき、空欄に入るどの数もその両隣の数の平均にすることができますか。理 由をつけてこたえなさい。

(栄光学園中）

とあることが「出来る」ことを説明するには、例を1つ挙げればよいのです。「出来ない」ことを説明するには、す こし考えなくてはいけませんね。

できない。

（理由）
異なる2つの数ＡとＢの平均の数は、
Ａ＞ＢのときＡより小さく、Ｂより大きい数である。

またＡ＜ＢのときＡより大きく、Ｂより小さい数となる。
つまり空欄の中にある異なる整数のうちの1つを考えたとき、
両側の数の平均であるということは、左右どちらかの数よりも大きく、
どちらかの数より小さいということになる。

しかし、8つの空欄にすべて異なる整数を入れるとき、
必ず「最大の数」が存在する。
その両側には、その数よりも小さい２つの数しか置くことができず、
間の最大の数をより小さな2つの数の平均にすることはできない。

以上の理由よりすべての空欄に異なる整数を入れ、
そのどの数も両隣の数の平均にすることはできない。

可能と不可能の説明は、
小学生の論理 性をはかるには格好の題材となります。

可能の証明は1つの例を挙げて終わりです。

ただし、不可能の説明には、高度な論理性が求められます。

反例を何個挙げても十分に説明したことにはならないということを、
事例を挙げながら理解させることが大切です。

これは中学生以降の証明問題への耐性を鍛えることに通じます。

類題を元にして、
教師、保護者の方々がしっかりと時間をかけて
説明することが必要な領域になります。

教室内で見られた別解として、
「1つの数ＡＣ の平均Ｂに関して、ＡとＢ、ＢとＣ の差は等しい。
するとＣ の隣のＤとその隣のＥとの差もそれぞれ等しくなり
8つの数の隣の数との差はすべて等しくなってしまう。・・・」

も上で解答として挙げたものとほぼ同数でした。

～今 回の問題から導かれる出題校からのメッセージ～
論理性に対する高い意識が大切

「自 分の立てた命題を、説明するために必要な要素は何なのか。」

中学生以降の高度な勉強、そして研究に関して、
これを見つけ出す感覚ほど重要であり、必要とされる素養は他にないといってもよいでしょう。

現在の中学受験のための塾の授業形態は圧倒的に
「インプット→自習による定着→テスト」というスタイルがとられています。

しかし、中学生以降の高いレベルの勉強において「答え」のみを提示し、
その正誤のみで評価されるような機会はほとんどありません。

入試に出ない から、などという理由で他者に対する説明能力を鍛えないことは、
入学以降の勉 強姿勢に大きく影響します。

またこの能力は普段から意識していなければ伸びることはありません。

本問は、東京大学など入試のほぼすべての問題が記述形式であり、
高い説明能力が求められる学校への合格率において、
圧倒的な結果を残している本校が求める人物像が見て取れる良問だと言えるでしょう。

渋谷幕張中より。未知/未習の問題の解答を推し量方法の基礎をここで勉強します。

　遺伝子は，生物の形や性質を，親から子へ伝えています。親子が似ているのは，遺伝子が受け継（つ）が れている証（あかし）です。しかし遺伝子のはたらきは，親から子へ形や性質を受け継ぐだけ ではありません。生物の体も，机やエンピツと同じように，いろいろな物質の集合体です。そして，生物の形や性質を決めているのは，タンパク質という物質で す。タンパク質は，細胞の構成成分であり，また酵素（こうそ）として体内のさまざまな化学 反応を進めています。

　一言でタンパク質と書きましたが，タンパク質には無限とも言えるほど多くの種類があります。私たちヒトの体も，何万種類ものタンパク質でできています。 しかし，どんなタンパク質にも共通していることがあります。それは，タンパク質がアミノ酸の集合体だと言うことです。

また，（1）タンパク質の材料となるアミノ酸は、どのような生物であっても20種類で共通してい ます。
　また，材料だけでなく、細胞がタンパク質を合成する基本のしくみは、動物、植物あるいは細菌まで，すべての生物で共通しています。タンパク質の種類にお いても，植物や動物，そして細菌まで，共通するものがたくさんあります。

　すべての生物は，自分が必要なタンパク質を，自分で合成します。そのときの設計図になるのが，遺伝子なのです。つまり生物は，合成するタンパク質の種類 の分だけ，遺伝子を持っているのです。

　親から子へ伝わる遺伝子の一部に変化があり，合成するタンパク質が変わると，生物の形や性質にも変化が表れてきます。生物は，長い年月をかけて，小さな 遺伝子の変化を積み重ねてきました。私たちヒトが一人一人ちがうのも，その結果なのです。

問
　下線（1）についてです。動物の体は，20種類すべてのアミノ酸をつくることはできません。　ヒトの成人の場合，体内でつくることができるのは12種類 です。
　では，植物の場合はどうでしょうか。適切なものを，次の（ア）～（ウ）から選びなさい。また，選んだ理由を，「植物は……。」という文で説明しなさい。

（ア）20種類すべてをつくることができる。
（イ）自分では1種類もつくれない。
（ウ）植物ごとにつくれる種類が異なる。

　　　　　　　　　　　　　　　　　　　　　　　　　
　　(渋谷教育学園渋谷幕張中　問題の一部を抜粋）

植物を構成するアミノ酸などもちろん未習だと思います。だからこそ、論理的に仮説設定および断定・論述をするのです。

記号： （ア）
理由：植物は、動物のように他生物をエサとして摂取することがないため、もしも自分でアミノ酸を全種類作れないと、すべてのアミノ酸を体内に取り入れるこ とができない。

シ ンプルでいい問題だと思います。

ポイントは、
・知らない問題にあたったときにあきらめずに思考をすすめられるか
・仮説をつかった論理展開　→　説明記述　ができるか
です。

自分の常識や感想を駆使すると、
「植物はいろいろな種類があるんだから、つくることのできるアミノ酸だっていろいろなはずだ」
と思ってしまうものですが。ここで、自分の主観にしばられない思考が必要なのです。

動物はアミノ酸20種類中、数種類しか作れない（ヒト成人で12種類）
↓
自分で作ることができないアミノ酸はどうやって得ている？？
↓↓
食料として、他のからとっているはず！

それでは、植物は、

もし、植物が20種類すべてのアミノ酸を作れないとしたら
↓
植物は（少数の食虫植物を除いて）エサをとらないので、自分で作れないアミノ酸を摂取できない

植物が作るアミノ酸や、そもそもアミノ酸って？？という
受験生でも、思考力により解答できる問題です。　

～今回の問題から導かれる出題校からのメッセージ～
仮説をもつことが出発点

ロ ジムではお馴染みのフレーズですが、

「知らない、習ってない」では何もすすみません。

手を止めずに、仮説設定→自分の知識・常識をつかった検証を、
多数かつ高速に繰り返すことができる人間こそが、中学校に求められる人材でないでしょうか。

さらに、仮説を検証し、解答を類推する過程で是非知っておいてほしいのが、
「もし～～だとすると」と仮定をおいて、その矛盾を説明し、「～～ではない」と
説明する方法です。

仮説設定・検証や、背理法による論理展開にしろ
年長者にとってのスキルのようですが、実は中学入試の世界でも
シビアにもとめられています。

そういったことを、近年人気急上昇の渋谷幕張中の
入試問題を通して実感してください。
（渋谷幕張２次の記述問題は、論理能力を試す良問ぞろいです）

市川中より。立体の問題ですが、求められるのは平面図形の高い分析能力です。

下の図は1辺4cmの立方体を点A、P、Qを通る平面と、点B、Q、Rを通る平面で切断し、2つの三角すいを切り取った立体です。この立体の表面積を求め な さい。ただし、点P、点Q、点Rはそれぞれ立方体の辺のちょうど真ん中の点です。

(市川中）

三角形PQAとQRBの面積がネックですね。直接求めることは出来ません。

表面積は

・底面と奥の正方形2枚（4×4）
・側面の台形2枚（上底2、下底4、高さ4）
・手前の三角形1枚（底辺4、高さ4）
・上部の五角形1枚（4×4の正方形から直角二等辺三角形2枚を切り取ったもの）
・切り口の三角形2枚

から構成されています。

底辺と高さが明らかでない切り口の三角形2枚の面積を求めます。
図は、立方体を真上から見た図です。

求めるべき切り口の三角形QRBと上部に作られる三角形QRCを比較する。

すると、
辺QRは二つの三角形に共通

QBとQCはともに正方形の一辺の中点から反対側の頂点に引かれた線であるため同じ長さ

RBとRCも同様

以上より三角形QRBと三角形QRCは、「3つの辺の長さが同じ」なので合同です。

もう1つの切り口の三角形PQAも同様。

よって切り口の2つの三角形の面積は、
上部に作られる三角形QRCの面積で代用します。

三角形QRCの面積は、

正方形（4×4）から直角三角形（2×4÷2）を2つと、
直角二等辺三角形（2×2÷2）

を1つ除いたものです。

よって面積は6平方センチメートル。

以上より

表面積は

底面と奥の正方形2枚：（4×4）×2枚＝32
側面の台形2枚：[（2＋4）×4÷2]×2枚＝24
手前の三角形1枚：4×4÷2＝8
上部の五角形1枚：4×4ー（2×2÷2）×2枚＝12
切り口の三角形2枚：6×2枚＝12

を合計して88平方センチメートル

答え：88平方センチメートル

昨年度の市川中の問題の中でも難問です。
切り口の三角形の面積については、誰もが着目し行き詰るでしょう。

ポイントは、

立体上の面積は、必ず平面にとらえなおすことです。

問題用紙に記載されている斜め上方からの図では、
感覚的にポイントとなる合同を見つけにくくなっています。

同じ長さの辺なども、そのような表記では違って見えるからです。

特に面積は相似、合同、比などの発見が突破口になります。
面倒くさがらずに面積問題として平面にする作業に取り組むことが大切です。

～今 回の問題から導かれる出題校からのメッセージ～
モデルの単純化が大切

立体ということで与えられた図だけを見ていても同様です。

そもそも立体であることは、
本問において惑わす要素にしかなっていません。

立体上の面積は、該当の部分を平面に書きおこすというのは定石ですが、
このように見た目に惑わされず本質のみを単純モデルとして考える思考法はとても大切です。

平面図形の面積の問題に取り組んでいるときは、
皆さん必ず相似合 同を考えるものですが、
立体上となるとと たんに頭の中から消えてしまうものなのです。

単純化することで、視界も広がり様々な方策が思い浮かびます。
トップクラスの生徒もこぞって受験する本校の最後の砦にふさわしい問題です。

合同に関しても三角形の合同条件がしっかり頭に入っていなければ
確信を持ちにくくしているところは、
平面に落とし込んだあとも確固たる力が求められる難問です。

麻布中より。簡単な図形の面積の公式を何パターンも思いつけますか。

下の図のように1辺10cmの正方形の内側で接している円と、その円周上に頂点がある正方形があります。内側の正方形の面積を求めなさい。

(麻布中）

正方形・円の面積はどのようにしてもとまるのだったでしょうか。

ポイントは、正方形の面積は「対角線×対角線÷２」でも求めることができることです。

内側の正方形の1辺は、求めることができません。

しかし対角線は、円の直径と同じであることがわかります。

そしてこの円の直径は、外側の正方形の1辺と同じ長さ、つまり10cmです。

内側の正方形の対角線が10cmであることから求める面積は
10cm×10cm÷2＝50平方センチメートル

答え：50 平方センチメートル

ここ数年、中堅・上位校の一行問題で流行の問題です。

円の面積を習い終わった４，５年生の時点でじっくり考えさせたい問題です。

円周率3.14の意味や、半径×半径の値との関係など、
円の面積を求める公式の要素一つ一つをしっかりと考えておくことでしか対応できません。

例えば、円の面積の公式の成立過程を理解していると、
半径と弧の長さだけでおうぎ形の面積を求めることができます。

このように、求積の公式の要素が、習ったとおりに素直に与えられていない問題は、
式の数学的な意味やほかの図形との関係性の理解力が問われます。

その週のテストに追われるように公式を覚えて済ましてしまっていると、
入試本番で痛い目にあいます。もう一度確認する機会にしてみてください。

～今回の問題から導かれる出題校からのメッセージ～
数式の意味を様々な角度から見る能力が大切

たとえば円の面積を求める公式：半径×半径×3.14を覚えたとします。

それでは、ある円が与えられたときに半径の長さがわからなければ
円の面積は求められないのでしょうか。

実は、半径は不明でも、「半径×半径」の値は求めることが出来る場合が数多くあります。

上記の公式の変数の部分を過不足なく把握しておくことで、
必要な条件を必要な形で探し当てることができます。

面積などの公式、そしてその公式の成立過程をしっかりと見直すことで
「どの値がわかれば算出できるのか。」という視野を広げておくことが大切です。

既存の知識として与えられたものを鵜呑みにせず
分解して確かめる姿勢は、
まさに麻布中の求める科学的な検証能力と同じものだということが出来るでしょう。