ロジムが「これは！」「一度はやっておかないと」と思った1問を紹介する、
ロジムメールマガジン「今週の1問」。
10月29日号の問題です。
（問題）
10％の濃さの食塩水が100グラムあります。この食塩水を70％の濃さにするためには食塩をどれだけ加えればよいですか。
（解答）
メールマガジンバックナンバーへ
（解説）
食塩の濃さに関する解法は様々なものがありますが、「濃さ」のイメージをしっかりと持たせることと、
食塩の濃さだけでなく、「水の濃さ」という視点を持つことが大切です。
食塩の濃さに限らず、全体を構成する要素の中で見落としがちなものは何かということを考える姿勢は大切です。
ふたのある容器に水を入れる問題で、水の体積だけでなく、水の入っていない部分の体積に注目するといった考え方です。
補集合に着目するということですね。
ロジカルシンキング第9回 （11/19、11/22、11/24, 11/25）
の受付を開始しました。
（申込ページ）
受講ご検討下さい。
講座内容
■「グラフ・図表の読み取り」 ～そこからいえること～
折れ線グラフと棒グラフの使い分けはできていますか？同じグラフでも性質は全く違い、グラフが作られた時点でグラフの作者による「グラフの種類選択」というメッセージがこめられています。
与えられた情報を効果的に伝えるには、どのグラフが使われるべきでしょうか。
入試問題でもグラフの読み取り・論述は頻出です。グラフの読み取りには、まずそもそもなぜその種類のグラフが選ばれたのかを考える必要があります。各種グラフがどういった情報に対して効果的かを学習し、グラフが持つ情報の分析方法を伝えます。
「連続的性のある論理展開（つながった思考）」に意識を置く、ロジカルシンキングのフレームを応用し、グラフの正確な読み取り→グラフが持つメインメッセージを抽出→グラフから考えられる自分の仮説構築 という本格的なグラフ読み取りのプロセスを経験します。
小学校3年・4年生向け
ロジカルシンキングクラスを
駒場東大前教室 土曜15時～17時
にて増設します。
学期途中ではありますが、各回完結の授業設定となりますので、お気軽に参加できます。
国語・算数・理科・社会 すべての科目の土台となるロジムの目玉クラスです。
お申込はこれまで同様、先着予約各回申込順となります。
（参考）「ロジカルシンキングとは」
以下、ロジムFAQページより
Q 「 ロジカルシンキングってなんですか？」
A 「物事の因果関係を考えること。それを筋道立てて他者に伝えること。」をロジムではロジカルシンキングと定義しております。」
Q 「ロジカルシンキングクラスの内容・スケジュールはどうなっています か？」
A 「ロジムホームページよりご確認ください。満席情報も適宜アップロードしております。」
Q 「考える力 」や「伝える力 」はどこで役にたつのですか？
A 「もっとも大きな効果として現れるのは、社会人として企業に就職したり、自らで起業したり、スポーツのスペシャリストとして国際舞台で活躍する際です。英語等他言語の習得も早くなります。また、身近なところでは、論理的な思考を修得することで科目学習や生活上の問題解決方法をより早く、そして深く身につけることができます。受験勉強にも必ず役に立ちます。」
Q 「小学生でもロジカルシンキングってできるものなんですか？」
A 「欧米では、幼児教育の現場からロジカルシンキングが取り入れられています。また、普段意識しなくても、「優秀な子」と呼ばれる生徒の多くが「論理的に物事を整理すること」「論理的に、つまり分かりやすく相手に物事を伝えること」を重視しています。」
Q 「ロジカルシンキングの授業を受けずに受験進学指導だけを受けたいのですが？」
A 「極力全員の方に「ロジカルシンキング」の授業を受けていただくようにしております。「ロジム」では、単なる受験進学指導 に終始しない、社会人になっても活きる学力を育むことを主旨としています。なにとぞご理解いただきたく思います。
また、4教科のどの授業でもロジカルシンキングの授業を受けていることを前提として、論理的思考によって答えを導いたり、理解を他者に説明することを求めます。」
Q 「ロジカルシンキングのクラスについてですが、1学期の授業と2学期の授業は同じことをやるのですか？」
A 「
・各テーマでの伝えたい内容の根底部分は変わりません
・テーマ内容を伝えるための、題材や演習・発表形式が違います
例えば、2学期のとある回の「もれなくだぶりなく」というテーマでは、
「物事の選択肢を網羅し、俯瞰することで、自分が解決すべき課題に、速く・正確に取り組める」
ということを根底として伝えます。これは1学期と同じです。ですが、それを考えるための題材や演習問題を1学期と違うものをご用意させていただきます。」
冬期講習 受付 開始
こんにちは。お待たせいたしました。
冬期講習の受付を開始いたします。
ロジムトップページのリンクから、もしくは、
http://www.lojim.jp/2007winter/2007winter.html
よりお申込下さい。
講座内容についてのお問合せについてもご遠慮なくどうぞ。
ロジムが「これは！」「一度はやっておかないと」と思った1問を紹介する、
ロジムメールマガジン「今週の1問」。
10月22日号は概算、和や単位あたりを考える感覚など、普段体系化することなく平坦に学習してしまう内容をもう一度考え直すのにとても適した問題です。
（問題）
箱の中に３と書かれたカードと５と書かれたカードがそれぞれたくさん入っています。この箱からカードを何枚か取り出し、書いてある数の合計を調べます。たとえば、合計９になるのは３のカードが３枚取り出される場合のみの１通りです。このとき合計２００３になる取り出し方は何通りありますか。
（解答）
メールマガジンバックナンバーへ
（解説）
様々な組み合わせを考える問題はまず極端な場合を考えて、どれくらいの範囲にあるのか、概算をすると見通しがよくなります。つるかめ算と同じ考え方です。本問はなるべく多くの5のカードを使う場合からスタートしても解くことができます。
また、次に取組むことになる「和を一定に保つ」ための作業は、いろいろな形に姿を変え出題されます。当然、増やした分を減らす、掛けた分を割るという還元作業をすればよいのですが、そう単純にはいきません。本問は減らすときには3が単位となり、増やすときには5が単位となります。このように、還元するときに単位が変わる（水を捨てるときと入れるときの単位時間当たりの水量が違うなど）のが常套なので、両者を丁寧にそろえる作業から手をつけていきましょう。
こんにちは。
明日（10/20土曜）、明後日（10/21日曜）はロジム休講日なので、ロジカルシンキング、通常授業ともに授業がありません。
スケジュール http://www.lojim.jp/schedule.pdf
ご注意下さい。
冬期講習のスケジュールがあらかた決まりました。
近日中にホームページにて告知いたしますので少々お待ち下さい。
ご事情で一刻も早く日程を知りたい方は、
予約はまだ出来ませんが、野村宛にメールを下されば、ご検討の講座について
お知らせいたします。
昨日告知いたしました無料コーチングセミナーですが、
満席につき申し込みを締め切ります。
キャンセル待ちは引き続き受付けますのでお問合せ下さい。
また増設の場合もこちらにて告知いたします。
こんにちは。
ロジムを会場として以下のような無料公開セミナーを行います。
企画の山本氏は野村の会社員時代の上司であり、公私にわたって多くのご指導をいただいています、いわばお師匠様です。経歴の迫力もさることながら、とてもわかりやすく物事を解説してくださり、バランス感覚が洋服を着て歩いていらっしゃるかのような落ち着いた物腰は、今も昔もこれからも野村の目標の人です。
従来の、問題解決方法を提示するコンサルティングと違い、「相手の中にこそ本当の答えがある」という手法をとるのが「コーチング」です。このコーチングを「保護者と生徒のコミュニケーション」に応用します。われわれの受験指導や保護者面談とは別の視点からの、皆様の問題意識解決へのヒントになればと思います。先着順ですのでお早めのお申し込みを。
株式会社ワイズクリエイト主催
「賢い子をそだてるコーチングセミナー」
■日時 2007年11月2日（金） 午前10時～12時
■会場 学習塾ロジム 門前仲町教室
■人数 先着順 満席になり次第締め切りとなります。
■申し込み info2@lojim.jp まで参加希望の旨をメール、または03-5646-5646 までお電話
■対象受講者 小学生保護者 （ロジム保護者以外の方もどうぞ）
■セミナー内容
子供の可能性を信じ、子供の能力を引き出しながら、親子の成長を目指します。
＜セミナーテーマ＞
・コーチングとは
・コーチングスキルの体験
・子供とのコミュニケーションで改善したい事
コミュニケーションの楽しさ、目標への意欲付け、コーチングのアプローチを体験します。脳を柔らかく持ち、話したいビジョンを持ち、具体的に話し合い、その場を楽しむワークショップです。家庭での双方向のコミュニケーションの活用をイメージしながら進行します。
■＜コーチ：山本宏義＞
慶應義塾大学工学部管理工学科修士課程修了
ソニー(株)入社。 経営管理・経営戦略などの業務を経験後、米国・英国に8年間駐在し、海外子会社の経営に参画する。 その間、ロンドン大学とスタンフォード大学でコミュニケーション論を学び、帰国後、米国系大手通信機器メーカーに転じ、営業マーケティング・経営戦略担当の役員を歴任後、2002年に(株)ワイズクリエイトを設立、代表に就任。
現在は、IT業界を中心に、組織力向上の為の経営コンサルティングに、問題解決型コーチング手法を
導入し、企業の組織開発と風土改革の為の支援活動をしている。
生涯学習開発財団認定コーチ
全国社外取締役ネットワーク会員
日本監査役協会会員
■＜株式会社ワイズクリエイト＞ http://www.yscoach.com/
企業向コーチングを約１０業種３０社以上で実施し、企業内のコミニュケーション改善を指導。
他には、学校教師、医者・看護士、美容室店長、外食チェーン店長へのコーチングを行い、チーム力を向上させる事で、やりがいのある職場環境づくりを目的として活動中。
共育コーチング研究会とのコラボレーションにより、保護者向けのコミニュケーションスキルカリキュラムを開発。
■コーチング に関する参考リンク
株式会社コーチ２１ http://www.coach.co.jp/
共育コーチング研究会 http://ciie.dreamblog.jp/
ロジカルシンキング第8回 （11/05、11/08、11/10, 11/11）
の受付を開始しました。
（申込ページ）
受講ご検討下さい。
講座内容
■「仮説思考」 ～未知の問題に対し思考を進める方法～
学校、塾での勉強、そして過程での多くの演習。数多くの問題をこなしているにもかかわらず、新しい問題に出会うと解けない、応用問題には手が出ない。
それは、仮説思考をしているかどうかの差です。
一つの問題に出会い考え、そして解答したうえで、「このことからいったい何が言えそうなのか」をつねに考えてみること。つまり自分なりの仮説をもって、演習を進めて行くことが、次に出会う問題が未知の問題に見えるのか、類題に見えるのかを決定します。授業では、「仮説をもつとはどういうことか」について、さまざまな情報を題材に取組み、体験してもらいます。
ロジムが「これは！」「一度はやっておかないと」と思った1問を紹介する、
ロジムメールマガジン「今週の1問」。
10月08日号は既に有名になりすぎて多くの小学生が答えを暗記してしまっている問題。「そもそもなんで？」も含めいい機会ですので考えて見ましょう。
（問題）
地球から見ると、月は自転をしているのに、月の裏側の模様が絶えず見えない理由を述べなさい。
（解答）
メールマガジンバックナンバーへ
（解説）
あまりに有名な問題ですが、一度はやはり出会っておくべき問題ですのでこの機会に。
月が自ら一回転してるうちに、地球の周りを一回転しています。
これは、文字で言われても理解しづらいので、下の図を参考に自分でノートに絵を書いてみてください。
（こういった、頭の中で物体を動かさなくてはいけない分野では教科書をじっとにらんでいても理解できた気になるだけで、身にはつきません。自分の手を動かし、紙の上で再現できて初めて理解できているとするべきです。）
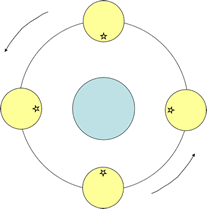
また、ここで疑問に思ってほしいこととして、
「なぜ、月の自転周期と公転周期がいっしょなの？もともとそうなの？それは偶然？」ということです。
これは、実は偶然ではなく、地球の重力により月はわずかですが楕円形になります。下の図を見ると分かりますが、楕円形の状態で、公転周期よりも自転周期がすこしでも遅くなったり早くなったりすると、楕円の月はわずかに斜めになり、月の重力とのバランスが悪くなります。
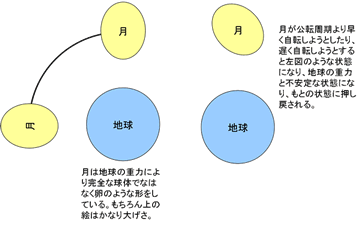
月が斜めになった瞬間に地球の重力によりまたバランスのいい状態に戻されます。これにより、自転周期と公転周期が同じになるように、いわば「調整」されます。
他にも、木星の衛星たちも自転周期と木星に対する公転周期が同じになっていたり、多くの衛星の自転周期と公転周期は1対１または、簡単な整数比になっているとのことです。
余談ですが、こういった理科の知識は、過去に一度でも「なんでだろう」と思ったことがあると、それを学習したときに深くそして長く記憶にとどめておくことが出来ます。どんな分野でもそうですが、普段から「なんでだろう」と思えるようになりたいものです。
また保護者の皆さんは、生徒に「なんでだろうね」と問いかけ、少しでも一緒に考えることが大切です。何か疑問をもったときそれを楽しそうに調べる親を見る生徒はやはり、疑問をもつことに対して前向きです。しかし、「わからないから塾の先生にきいといで」とあしらい、普段疑問をもつことに楽しそうにしない両親から「普段から疑問を持つことが大切だよ。なんでなんでと思いなさい。」と言われても、そんなの習慣になるわけはありません。
塾講師の言うことではないかもしれませんが、生徒の習慣は確実に親の習慣と似ます。何でうちの子は・・・ という前に、まず保護者の皆様がご自身の「知に対する姿勢」を考え直してみてください。